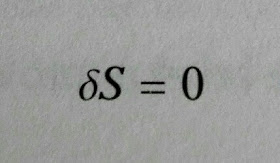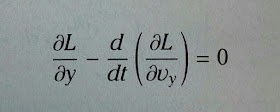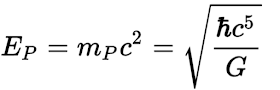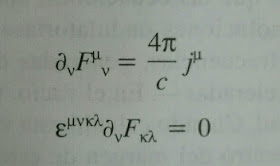Esta entrada está basada en el apéndice del Libro El Gran Cuadro, escrito por el físico teórico y cosmólogo norteamericano de Sean Carroll
La teoría del núcleo es una teoría cuántica de campos que describe la dinámica e interacciones de cierto conjunto de partículas de materia (fermiones) y partículas de fuerzas (bosones), incluyendo tanto el modelo estándar de la física de partículas como la teoría general de la relatividad (en el régimen de gravedad débil).
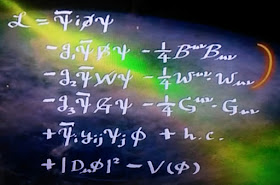
Lagrangiana del modelo estándar a partir de la cual pueden explicarse todos los fenómenos salvo los relacionados con la gravedad
Ecuaciones de campo de la Relatividad General que proporcionan las gμν que caracterizan la geometría y la métrica el espacio-tiempo creado por una distribución de masa-energía concreta
La teoría del núcleo se basa en la fórmula de la integral de caminos de la mecánica cuántica, propuesta por Richard Feynman. Esta fórmula resume todo lo que hay que saber sobre la dinámica cuántica de este modelo: partiendo de una configuración inicial de campos, ¿qué probabilidad hay de que estos campos acaben en alguna configuración distinta en un instante posterior?
Formulación de la integral de camino o de suma de historias de la mecánica cuántica propuesta por Richard Feynman
El principio de mínima acción nos dice que las ecuaciones de movimiento surgen de minimizar una magnitud física llamada acción
Las
ecuaciones de Euler-Lagrange obtenidas mediante el cálculo de
variaciones proporcionan el lagrangiano L que minimiza la acción
El valor de la acción determina la probabilidad de cada una de las historias posibles para un suceso en mecánica cuántica.
Hay dos clases de campos cuánticos: fermiones y bosones. Los fermiones son las partículas de la materia, ocupan espacio lo que proporciona estabilidad y solidez a la materia. Los bosones pueden apilarse unos encima de otros, originando campos de fuerza macroscópicos como la gravedad y el electromagnetismo.
En teoría cuántica de campos las partículas son en realidad vibraciones de campos cuánticos y quedan determinadas por su masa, carga, momento angular y espín. Las cargas determinan cómo interactúan las partículas entre sí. La carga de una partícula nos indica como interactúa con el campo portador de la fuerza asociada. Así:
- los electrones (carga eléctrica -1) interactúan directamente con los fotones, portadores de la fuerza electromagnética.
- los neutrinos, que tienen carga eléctrica nula, no interactúan directamente con los fotones pero sí indirectamente mediante los electrones.
- Los fotones mismos son neutros, así que no interactúan directamente entre sí.
La carga gravitacional es solo la energía de la partícula, que es igual a la masa multiplicada por la velocidad de la luz al cuadrado cuando la partícula está en reposo. Esta carga es universal, la poseen todas las partículas.
Equivalencia entre masa y energía de la relatividad especial
Todos los fermiones tienen una carga nuclear débil, por lo que interactúan con los bosones W y Z.
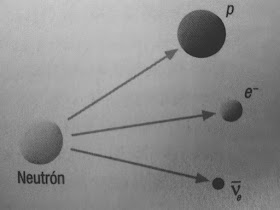
La fuerza nuclear débil es la responsable de la desintegración beta en la que un neutrón se transforma en un protón más un electrón más un antineutrino
Diagrama de Feynman de la desintegración beta en la que un bosón W se lleva una unidad negativa de carga y se acaba desintegrando en un electrón y un antineutrino
Los fermiones que interactúan con la fuerza nuclear fuerte son lo quarks, y los que no, los leptones (electrones y neutrinos).
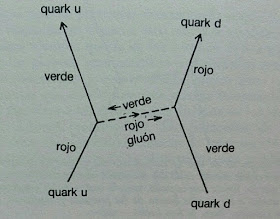
Interacción entre un quark up y un quark down mediante el intercambio de gluones
La fuerza nuclear fuerte es tan fuerte que quarks y gluones se ven confinados dentro de partículas como protones y neutrones, por lo que nunca los observamos directamente.
Los hadrones formados por tres quarks se llaman bariones y los mesones son partículas formadas por un quark y un antiquark
Luego está el campo de Higgs y su partícula asociada, el bosón de Higgs, descubierto en el LHC (Large Hadron Collider o Gran Colisionador de Hadrones) en 2012.
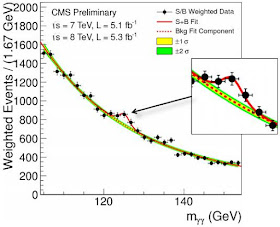
Resultado del CMS para el canal de desintegración de dos fotones. La pequeña prominencia en la curva es el bosón de Higgs, a unos 125 GeV (CERN/CMS)
CMS, Solenoide Compacto de Muones, es uno de los experimentos del Gran Colisionador de Hadrones en el CERN, en la actualidad el acelerador más potente del mundo
Aunque es un bosón, normalmente no hablamos de una fuerza asociada al campo de Higgs; podríamos, pero el Higgs es tan grande, que la fuerza correspondiente es extremadamente débil y de corto alcance. Lo que hace tan especial al bosón de Higgs es que su campo tiene un valor distinto de cero incluso en el espacio vacío. Todas las partículas nadan constantemente en un baño de Higgs, y eso afecta a sus propiedades. Lo más importante es que otorga masa a los quarks y a los leptones cargados, así como a los bosones W y Z.
Las partículas elementales del Modelo Estándar se agrupan en 3 familias. En esta imagen cada familia corresponde a las partículas de las primeras dos columnas de la izquierda, las dos columnas centrales y las dos columnas de la derecha
La función de onda describe una superposición de cada configuración posible del sistema con el que se está trabajando. Para la teoría del núcleo, una configuración es un valor particular para cada campo, en cada punto del espacio.
La versión de Feynman de la evolución cuántica (que es equivalente a la de Schrödinger) nos indica la probabilidad de que el sistema termine en una configuración determinada dentro de la función de onda, dado que empezó en algún momento precedente en una configuración diferente dentro de una función de onda anterior.
Ecuación de Schrödinger donde H es el operador hamiltoniano
La amplitud W es determinada por la integral de caminos de Feynman sumando todas las formas en que podrían evolucionar los campos entremedias.
Formulación de la integral de camino o de suma de historias de la mecánica cuántica propuesta por Richard Feynman. En la exponencial compleja está incluida la lagrangiana del modelo estándar y la de la relatividad general (para campos gravitatorios débiles)
¿Y qué es exactamente lo que estamos sumando? Para cada posible camino que puede tomar un sistema, hay una magnitud que calculamos, llamada acción, S. Si el sistema está saltando de cualquier manera por todas partes, su acción será muy grande; si se mueve más uniformemente, la acción será relativamente pequeña. Tanto en mecánica clásica como en mecánica cuántica, de todos los posibles caminos, el sistema toma el que tenga asociada una mínima acción. Toda teoría clásica puede definirse diciendo cuál es la acción del sistema, y luego buscando movimientos que la minimicen.
En la mecánica cuántica, la acción aparece de nuevo, pero con un giro. Feynman propuso un enfoque en el que podemos pensar que un sistema cuántico sigue todos los caminos, no solo el clásicamente permitido. A cada camino le asociamos un cierto factor de fase:
e{iS}
que es un número complejo. Sumar todas las contribuciones para todos los caminos puede implicar una suma constructiva o destructiva.
Patrón de interferencia en el experimento de la doble rendija debido a la suma de los diferentes caminos
La excepción se produce cuando un grupo de caminos próximos tienen valores muy similares para la acción; sus factores de fase serán entonces similares, y sumarlos supondrá su acumulación, en lugar de anularse. Esto sucede exactamente cuando la acción se halla cerca de un valor mínimo, que corresponde al camino permitido clásicamente.
Así pues, la mayor probabilidad cuántica queda asociada a una evolución de apariencia casi clásica. Por eso es por lo que nuestro mundo cotidiano está bien modelizado por la mecánica clásica; es el comportamiento clásico el que aporta las mayores contribuciones a la probabilidad de las transiciones cuánticas.
Las cantidades [Dg][DA][Dψ][Dφ] significan cantidades infinitesimales de:
g: el campo gravitatorio.
A: campos de fuerzas bosónicos (electromagnetismo, fuerzas nucleares fuerte y débil).
ψ: campos fermiónicos.
φ: el bosón de Higgs.
Es decir, gravedad, otras fuerzas, materia y Higgs.
Todo lo que sigue a la unidad compleja i es la acción S para la teoría del núcleo.
La acción es una integral sobre la totalidad del espacio, y sobre el período de tiempo entre la configuración inicial y la final. Es decir, sobre las cuatro dimensiones del espacio-tiempo. El factor raíz cuadrada de -g está relacionado con el hecho de que el volumen no es un invariante en la relatividad especial ni general. Depende del movimiento del observador y de la curvatura del espacio-tiempo.
El término gravedad es bastante simple, reflejando la elegancia de la teoría de la relatividad general de Einstein. La cantidad R recibe el nombre de curvatura escalar y representa cuánta curvatura espacio-temporal de cierta clase está presente en cualquier momento dado.
Según la relatividad general la masa de una estrella como el Sol curva el espacio-tiempo tiempo haciendo que los planetas orbiten a su alrededor al seguir el camino más corto posible (geodésica) en un espacio-tiempo de cuatro dimensiones
La curvatura escalar se multiplica por una constante igual a un medio de la masa de Planck al cuadrado.
Masa de Planck
Energía de Planck
La curvatura escalar R puede calcularse a partir del campo gravitatorio, y la acción para la relatividad general es simplemente proporcional a la integral de R sobre una región de espacio-tiempo. Minimizar esa integral nos da la ecuación de campo de Einstein para la gravedad.
El término otras fuerzas incluye el tensor de fuerza F, que incluye las contribuciones del electromagnetismo y de las fuerzas nucleares fuerte y débil.
Ecuaciones de Maxwell en notación tensorial
Ecuaciones de Maxwell en formato diferencial y vectorial
Los campos de materia son fermiones, representados colectivamente con la letra ψ. En el primero de los dos términos de materia, la letra γ indica las matrices de Dirac, origen de la existencia de las antipartículas. La letra D representa la derivada covariante que incluye el acoplamiento o interacción entre fermiones y los bosones de fuerza. Esta interacción depende de cómo estén cargados los fermiones. La forma en que un electrón interactúa con un fotón, por ejemplo, la caracteriza este término de la acción.
Ecuación de Dirac para una dimensión espacial donde aparecen las matrices γ
El segundo término de materia indica un acoplamiento entre los fermiones y el campo de Higgs. A diferencia del resto de la acción de la teoría del núcleo, la interacción entre el Higgs y los fermiones resulta un tanto barroca y poco atractiva.
Dos cosas la hacen complicada:
- La primera es la matriz de mezclas Vij que recuerda el hecho de que los fermiones pueden mezclarse entre sí; cuando un quark cima decae, por ejemplo, en realidad decae en una mezcla particular de quarks down, strange y bottom.
- La otra dificultad es que un campo de fermiones es zurdo y el otro diestro. Esto es consecuencia de que la naturaleza trata de forma diferente a las partículas zurdas y diestras. Ese fenómeno, la violación de la paridad, constituyó toda una sorpresa para los físicos cuando se descubrió, aunque en la actualidad y con un conocimiento más profundo del mundo subatómico no se considera tan excepcional.
La última parte de este término, h.c. representa el conjugado hermitiano. Esto es necesario porque necesitamos quedarnos con la parte real porque la acción debe ser un número real.
Finalmente tenemos la parte de la acción dedicada al campo de Higgs. La primera parte es el término cinético que representa la tasa de cambo del campo, y la segunda es el término potencial, que representa cuánta energía encierra el campo incluso cuando no está cambiando en absoluto. Es este segundo término el que hace que el campo de Higgs sea especial. Como cualquier otro campo quiere permanecer tranquilo en una configuración de mínima energía. Pero a diferencia de los otros campos conocidos, en su estado de energía mínima, el campo de Higgs mismo no desaparece, sino que tiene un valor distinto de cero. Su energía potencial es mayor cuando el campo es nulo que cuando no lo es. Eso es lo que le asegura al campo de Higgs una presencia incluso en el espacio vacío y le permite afectar a todas las demás partículas que se desplazan por él.
A la izquierda el potencial de Higgs es nulo cuando el campo de Higgs también lo es. Sin embargo a la derecha se rompe esta simetría y el potencial es diferente de cero cuando el campo de Higgs es nulo
Sabemos que la teoría del núcleo no puede ser la respuesta definitiva. En el universo hay materia oscura que no encaja bien en ninguno de los campos conocidos.
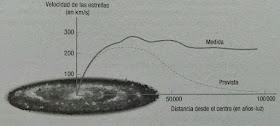
La materia visible se insuficiente para explicar el movimiento de las estrellas periféricas de las galaxias y requeriría de un nuevo tipo de materia para ser explicado
Por otro lado los neutrinos tienen masa pero aún no hemos verificado experimentalmente que los términos existentes en la ecuación sean de hecho responsables de la masa de los neutrinos.
Prácticamente todos los físicos creen que hay más partículas y campos por descubrir, con mayores masas y energías. Pero tienen que ser unos que, o bien interactúan muy débilmente con nosotros (como la materia oscura) o bien decaen muy deprisa.
La teoría del núcleo ni siquiera proporciona una teoría completa de los campos conocidos. La ecuación funciona si el campo gravitatorio es muy débil, pero no funciona cuando la gravedad es intensa, como en las cercanías del Big Bang o en el interior de un agujero negro. Para estos casos se necesita una teoría de gravedad cuántica.
El espacio-tiempo se curva de manera extrema en un agujero negro haciendo necesaria una teoría de gravedad cuántica
De todas maneras, esto no es problemático porque las limitaciones de la teoría están incorporadas en su formalismo. Con k<Δ (corte ultravioleta) se indica la limitación a los campos que no vibran demasiado enérgicamente. Los campos pueden verse como una combinación de modos, siendo cada uno de estos modos una vibración con una longitud de onda específica. Esto significa situaciones de baja energía y campo débil, pero suficiente para describir nuestro mundo cotidiano que es de baja energía.
La teoría del núcleo es, en otras palabras, una teoría de campo efectiva. Tiene un régimen de aplicabilidad muy específico y bien definido (partículas que interactúan con energías muy por debajo del corte ultravioleta) y no afirmamos que sea fiable más allá de eso. Aún así es extremadamente precisa, rígida y bien definida. No hay ambigüedad alguna en ella, ni espacio para introducir nuevos aspectos que aún no hayamos advertido.
Quizás en el futuro encontremos una teoría más exhaustiva subyacente a la teoría del núcleo que no aluda a la teoría cuántica de campos. Pero nada de eso cambiará el hecho de que la teoría del núcleo es una descripción exacta de la naturaleza en su dominio de aplicabilidad.