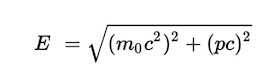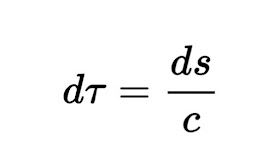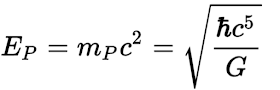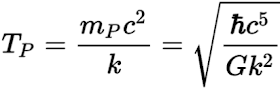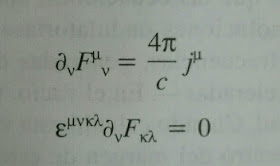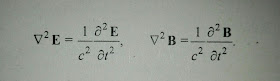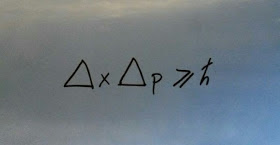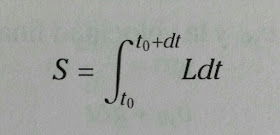El Universo Cuántico es un muy buen libro sobre física cuántica escrito por Brian Cox y Jeff Forshaw. Este sería un resumen de dicho libro.
Índice
1. Aquí pasa algo raro
2. Estar en dos lugares a la vez
3. ¿Qué es una partícula?
4. Todo lo que puede suceder, sucede
5. El Movimiento como una ilusión
6. La música de los átomos
7. El Universo en la cabeza de un alfiler
8. Interconectados
9. El mundo moderno
10. Interacción
11. El espacio vacío no está tan vacío
Energía en función del momento. Esta ecuación es usada sobretodo en Mecánica Cuántica Relativista
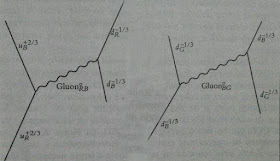
Fuerzas entre quarks a partir del intercambio de dos gluones virtuales
Un electrón se transforma en un neutrino electrónico a la vez que un quark up se convierte en un quark down. Dos versiones del mismo diagrama de Feynman
Dispersión de un neutrino electrónico en un quark down
La interacción de un bosón gauge débil W con su antipartícula puede originar un bosón gauge débil neutro Z
Camino alternativo por el que el electrón puede ir de un sitio a otro que debe considerarse para obtener una mejor aproximación del momento magnético de un electrón
Diagrama de Feynman de una primera aproximación para calcular el momento magnético del electrón
Una de las predicciones de la relatividad general es la curvatura de los rayos luminosos al pasar cerca de una estrella como el Sol
Recreación del Big Bang como choque de dos branas de tres dimensiones que viven en un espacio de más dimensiones
En la teoría de Kaluza-Klein la quinta dimensión esta enrollada sobre sí misma con un radio diminuto
El electrón y el protón se mantienen unidos mediante el intercambio constante de fotones
Las dualidades debil-fuerte y radio grande-pequeño crean una red de conexiones que interrelacionan y fusionan las cinco teorías de cuerdas, la supergravedad en once dimensiones y la Teoría M en un marco unificado.
La dualidad grande/pequeño del radio completa la red de conexiones resultando que las cinco teorías de cuerdas, junto con la Teoría M, son duales entre sí.
Las diferentes teorías de supercuerdas son en el fondo soluciones particulares de una teoría más profunda llamada teoría M
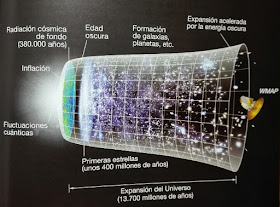
Cronológia del Big Bang
Las órbitas de los planetas del Sistema Solar fueron descritas por primera vez por la Ley de Gravitación Universal
El ATLAS es un detector de partículas ubicado en las instalaciones del Gran Colisionador de Hadrones (LHC). Se utiliza para buscar posibles pruebas relacionadas con el origen de la masa y con la existencia de dimensiones adicionales
Montaje del calorímetro del detector ATLAS del LHC. Los ocho imanes toroidales rodean al calorímetro, que mide la energía de las partículas que se producen cuando los protones colisionan en el centro del detector
CMS, Solenoide Compacto de Muones, es uno de los experimentos del Gran Colisionador de Hadrones en el CERN, en la actualidad el acelerador más potente del mundo
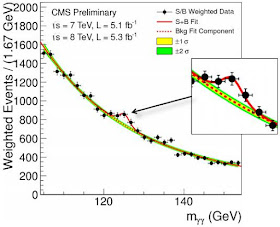
Resultado del CMS para el canal de desintegración de dos fotones. La pequeña prominencia en la curva es el bosón de Higss, a unos 125 GeV (CERN/CMS)
Expansión del universo tras el Big Bang
Ejemplo de dimensiones extra compactificadas, en este caso en forma de esfera
El principio de equivalencia se basa en la igualdad entre masa gravitatoria y masa inercial
Espacio-tiempo de Minkowski
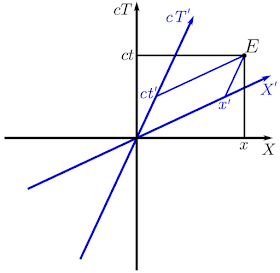
Espacio-tiempo de Minkowski de 2 dimensiones: una espacial y una temporal. En negro se dibuja un sistema de coordenadas y en azul, otro con velocidad relativa v. E es un evento referido a las coordenadas de ambos sistemas
El tiempo propio de la relatividad especial se define como el intervalo relativista entre la velocidad de la luz
El espacio-tiempo se curva de manera extrema en un agujero negro
Agujero de gusano o puente de Einstein RosenLos agujeros de gusano como conexiones entre dos regiones alejadas del espacio-tiempo son soluciones permitidas por la Relatividad General, aunque altamente inestables
Dilatación gravitacional del tiempo donde T0 es el tiempo propio y T es el tiempo para un observador externo. Si R es igual al radio de Schwarzschild, T tiende a infinito. Si R es muy grande, T es equivalente a T0
Tiempo de Planck
Masa de Planck
Longitud de Planck
Energía de Planck
La temperatura de Planck es de 1032K y era la temperatura aproximada en el tiempo de Planck
Energía radiada por un agujero negro en rotación
Fusión de dos agujeros negros en el que el horizonte del agujero negro resultante se comporta como un fluido de quarks
Temperatura de un agujero negro
Uno de los mecanismos físicos que explicaría el origen de la radiación de Hawking sería la creación de un par de partículas virtual cerca del horizonte de un agujero negro. Una de ellas cae en el agujero negro y la otra es emitida como radiación de Hawking
Lagrangiana de la Electrodinámica Cuántica, la teoría que describe como interacciona la luz con la materia. M es la masa del electrón, A es el potencial vector del electromagnetismo y F es el tensor electromagnético. Los dos primeros corresponden a la ecuación de Dirac, el tercero es el de interacción entre el electrón y el fotón (consecuencia de la simetría gauge) y el cuarto es el de la propagación del fotón en ausencia de fuentes (onda electromagnética)
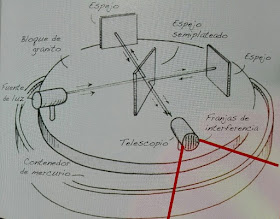
Interferómetro diseñado por Michelson con el que demostraron que el éter no existía
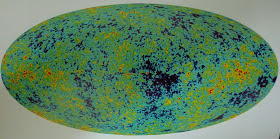
Antena en forma de cuerno o bocina con la que Penzias y Wilson descubrieron la radiación del Fondo Cósmico de Microondas
Ecuaciones de Maxwell en notación tensorial
Aproximación de la energía relativista a bajas velocidades (cuando v es mucho menor que c)
1. Aquí pasa algo raro
La mecánica cuántica es uno de los tres grandes pilares de la física, que serían:
- La mecánica cuántica.
- La relatividad especial, que explica la naturaleza del espacio-tiempo.
Equivalencia entre masa y energía de la relatividad especial
- La relatividad general, que explica la gravedad.
Ecuaciones de campo de la Relatividad General que proporcionan las gμν que caracterizan la geometría y la métrica el espacio-tiempo creado por una distribución de masa-energía concreta
Según la relatividad general la masa de una estrella como el Sol curva el espacio-tiempo tiempo haciendo que los planetas orbiten a su alrededor al seguir el camino más corto posible (geodésica) en un espacio-tiempo de cuatro dimensiones
Su precisión y capacidad de predicción son enormes. Como ejemplo, la predicción del movimiento de un electrón cerca de un imán (momento magnético) como prueba de la exactitud de la electrodinámica cuántica.
La mecánica cuántica reduce la complejidad del mundo a una descripción del comportamiento de un conjunto de partículas y las cuatro fuerzas que actúan entre ellas. La teoría cuántica surgió como explicación de fenómenos naturales a principios del siglo XX que las teorías de la época no podían explicar. Sus precursores fueron: Rutherford, Bohr, Planck, Einstein, Pauli, Heisenberg, Schrödinger y Dirac.
El adjetivo cuántico procede de cuanto, nombre que Planck asignó a los paquetes de energía resultantes de su hipótesis de discretización de la energía para explicar la radiación del cuerpo negro en el año 1900. Está hipótesis se vio reforzada posteriormente por la explicación de Einstein del efecto fotoeléctrico en 1905.
A lo largo de la historia se han ido proponiendo varios modelos para la luz:
- Planck y Newton afirmaban que la luz era un flujo de partículas.
- Maxwell (1864) afirmó que la luz es una onda electromagnética.
- Compton (1925) analizó choques entre cuantos y electrones concluyendo que estas colisiones revelaban que los electrones se comportan como partículas.
Ecuaciones de Maxwell
Ecuación de onda electromagnética para los campos eléctrico y magnético
Sin embargo la luz se comporta como onda y como partícula. Esto es el fin de la física clásica y el fin del principio de la mecánica cuántica. En 1926 se confirmó que los fotones eran cuantos.
2. Estar en dos lugares a la vez
Una cronología de los inicios de la mecánica cuántica sería:
1895
Röntgen descubre los rayos X. Aunque es el siglo XIX, a nivel de la física es el punto en el que comienza el siglo XX porque fue el detonante de todos los descubrimientos de principios de este siglo.
1896
Bequerel descubre la radioactividad en París, que puede ser considerado como el inicio de la revolución cuántica. Lo desconcertante de la desintegración radiactiva es que es espontánea e impredecible. La vida de los átomos toma aleatoriamente todos los valores entre 0 e infinito. Son las primeras muestras aleatorias del micromundo. Hasta este punto, todo en la ciencia era determinista. Sin embargo, la teoría cuántica trata con probabilidades en lugar de con certezas.
1911
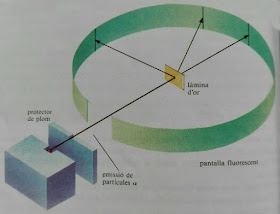
Rutherford propone un modelo del átomo con un núcleo pequeño y electrones orbitando lejos alrededor. La masa del átomo está casi toda en el núcleo, lo que hace que una de cada 8000 partículas alfa rebote en él. Los átomos son prácticamente espacio vacío. Los problemas de este modelo es que los electrones orbitando debían perder energía y caer al núcleo en espiral porque las cargas radian en trayectoria acelerada, como lo es el movimiento curvo.
Experimento de Rutherford en que se lanzaban partículas alfa contra una fina lámina de oro y se observaba su trayectoria
1913
Modelo del átomo de Bohr. Sus características principales son:
- Solo se permiten un conjunto concreto de órbitas para los electrones. Las más cercanas al núcleo son las de menos energía.
- Los electrones saltan entre órbitas al recibir energía. Emiten luz al volver a una órbita inferior de color determinado por la diferencia de energía entre órbitas.
- Cada átomo tiene un conjunto característico de órbitas, es decir, tiene una especie de huella espectral.
Los problemas del modelo de Bohr eran:
- ¿Qué impide que los electrones caigan al núcleo cuando deberían perder energía por radiación electromagnética?
- ¿Por qué estaban cuantizadas las órbitas de los electrones?
- ¿Qué pasaba con elementos más pesados que el hidrógeno? ¿Cómo se entendía su estructura?
El modelo de Bohr busca dar una explicación al experimento de Angstrom en 1853 en que provoca descargas eléctricas en tubos de hidrógeno. Tras estas descargas, solo se observa luz roja, verde azulada y violeta. Cada elemento químico tiene un código de barras de colores específico.
1925
Heisenberg introduce una nueva manera de entender la teoría de la materia y las fuerzas. Es una teoría basada solo en las relaciones entre magnitudes que, en principio, pueden observarse. El objetivo de la teoría cuántica debe ser predecir cosas observables: como la luz emitida por el hidrógeno. Por tanto se debían abandonar los prejuicios de lo que sucede a escala microscópica.
Heisenberg introduce una nueva manera de entender la teoría de la materia y las fuerzas. Es una teoría basada solo en las relaciones entre magnitudes que, en principio, pueden observarse. El objetivo de la teoría cuántica debe ser predecir cosas observables: como la luz emitida por el hidrógeno. Por tanto se debían abandonar los prejuicios de lo que sucede a escala microscópica.
En este punto, se sabe que la teoría cuántica tiene las siguientes características:
- Las partículas cuánticas no se están quietas. Saltan de un sitio a otro incluso en ausencia de fuerzas.
- El propio concepto de fuerza no forma parte de la teoría cuántica.
- La física de Newton surge de la descripción cuántica. Todo es cuántica independientemente del tamaño.
- En la teoría cuántica la magnitud dinámica principal es el momento (p=mv) y su conservación en lugar de la fuerza.
- Las constantes más importantes en la teoría cuántica son h y c.
- En teoría cuántica los objetos están en más de un lugar a la vez y no es posible medir con precisión como se mueven.
Principio de Incertidumbre de Heisenberg
1927
Experimento de la doble rendija de Davisson y Germer con electrones. Se observa un patrón de interferencia aunque los electrones se disparen de uno en uno. Un electrón se interfiere consigo mismo. Además el patrón no va surgiendo a medida que impactan los electrones en la pantalla, sino desde el primer impacto. Los demás impactos aumentan la intensidad del patrón. Además el patrón está formado por puntitos, uno por cada electrón. Aunque los electrones tienen masa y carga definidas, no se comportan exactamente ni como partículas ni como ondas.
Experimento de la doble rendija de Davisson y Germer con electrones. Se observa un patrón de interferencia aunque los electrones se disparen de uno en uno. Un electrón se interfiere consigo mismo. Además el patrón no va surgiendo a medida que impactan los electrones en la pantalla, sino desde el primer impacto. Los demás impactos aumentan la intensidad del patrón. Además el patrón está formado por puntitos, uno por cada electrón. Aunque los electrones tienen masa y carga definidas, no se comportan exactamente ni como partículas ni como ondas.
Patrón de interferencia en el experimento de la doble rendija
La mecánica cuántica no aplica solo a lo muy pequeño. Es necesaria para explicar el final de las enanas blancas y su masa máxima de 1.4 veces la masa del Sol, o límite de Chandrasekhar. También es necesaria para explicar la entropía de los agujeros negros.
La entropía de un agujero negro es igual a un cuarto del área del horizonte de sucesos en unidades de Planck, en que una longitud de Planck al cuadrado es lP2= hG/2πc3
3. ¿Qué es una partícula?
Supondremos que los componentes más fundamentales de la naturaleza son partículas. La primera pregunta sería: ¿Cómo se mueven las partículas de un lugar a otro? El experimento de la doble rendija exige que las partículas sean extensas, que estén en varios lugares a la vez para que puedan interferirse consigo mismas. En un primer momento podríamos pensar en una "onda de electrón" como perturbaciones materiales reales. Pero no explicarían los puntitos discretos en la pantalla. Hay que reinterpretar la onda de electrón como información de la probabilidad de donde puede estar el electrón. La única función de la onda de electrón es permitir calcular la probabilidad de que el electrón incida en la pantalla en un determinado punto. En cada instante el electrón está descrito por una onda. Debemos permitir que la onda de electrón atraviese ambas rendijas para obtener el patrón de interferencia, lo que implica que debemos permitir todos los recorridos posibles del electrón entre la fuente y la pantalla. El electrón parte de la fuente siguiendo a la vez todos los caminos posibles. En mecánica cuántica, lo que no está prohibido es obligatorio.
Sabemos que las ondas se interfieren entre sí cuando tienen fases diferentes. Para representar la fase de una onda podemos utilizar un reloj o fasor: la longitud de la manecilla es el módulo del fasor y la hora es la fase, habiendo 2π posibilidades para esta. La distancia entre dos picos o valles de la onda es la longitud de onda. Si dos ondas iguales se desfasan entre sí 180 grados se cancelan mutuamente.
La suma de relojes sigue las mismas reglas que la suma de los números complejos. Por ejemplo, en el caso de las ondas de agua, solo importa la altura de las ondas, con lo que los relojes no son necesarios. En el caso de las partículas cuánticas sí son necesarios. Si la temperatura de una habitación puede describirse mediante un campo de temperaturas donde a cada punto le corresponde un número real, en el caso de una partícula cuántica, se necesita un campo de fasores o números complejos con un reloj en cada punto. Este conjunto de relojes forman la función de onda cuyo módulo al cuadrado indica la probabilidad de que en ese punto se encuentre la partícula.
La suma de relojes sigue las mismas reglas que la suma de los números complejos. Por ejemplo, en el caso de las ondas de agua, solo importa la altura de las ondas, con lo que los relojes no son necesarios. En el caso de las partículas cuánticas sí son necesarios. Si la temperatura de una habitación puede describirse mediante un campo de temperaturas donde a cada punto le corresponde un número real, en el caso de una partícula cuántica, se necesita un campo de fasores o números complejos con un reloj en cada punto. Este conjunto de relojes forman la función de onda cuyo módulo al cuadrado indica la probabilidad de que en ese punto se encuentre la partícula.
En 1926 Erwin Schrödinger introduce la función de onda pero no la interpreta correctamente. Lo hace Max Born afirmando que su módulo al cuadrado proporciona la probabilidad. Esta probabilidad no se debe a la falta de información, es algo fundamental. No se puede predecir la posición de una partícula, se puede predecir la probabilidad.
Ecuación de Schrödinger donde H es el operador hamiltoniano
En 1926, Max Born afirma que el movimiento de las partículas sigue leyes de probabilidad, pero la probabilidad en sí se propaga de forma determinista según la ley de causalidad.
4. Todo lo que puede suceder, sucede
Una partícula puede entenderse como un conjunto de relojes o flechas diseminados. Conjuntamente forman la función de onda, cuyo módulo al cuadrado proporciona la probabilidad de que la partícula se encuentre en un estado concreto. Una partícula puede autointerferirse tal y como muestra el experimento de la doble rendija debido a la suma de relojes que no marcan la misma hora (o flechas con direcciones diferentes).
¿Cómo evolucionan los relojes con el tiempo en ausencia de fuerzas? Las leyes de Newton dirían que si estaba en reposo, seguirá en reposo. Si estaba en movimiento rectilíneo uniforme, seguirá con este movimiento. Sin embargo, lo correcto es afirmar que en un instante posterior, la partícula puede estar en cualquier lugar del universo. Esto equivale a que no podemos saber nada sobre su movimiento. Esto no contradice la teoría de la relatividad porque esta dice que es la información la que no puede viajar más rápido que la luz y esto también aplica a la teoría cuántica. De hecho, la dinámica correspondiente a una partícula que atraviesa el universo de un salto es completamente opuesta a la transferencia de información, porque no podemos saber de antemano a donde saltará la partícula.
La regla fundamental de la teoría cuántica consiste en transportar todos los relojes o flechas iniciales al punto donde queremos calcular la probabilidad de que se desplace, y luego sumarlos todos usando la regla para la adición de relojes. La regla para el cambio de fase o dirección de la flecha es Ldt, siendo L el lagrangiano. Esta cantidad se llama acción y la naturaleza hace uso de ellas de manera fundamental. Esto lo intuyó el matemático Leonhard Euler quien formuló el principio de mínima acción: "La trayectoria de un cuerpo es tal que la acción calculada entre dos puntos cualquiera de la misma es mínima". Este principio es una manera alternativa de obtener las leyes de movimiento de Newton.
Paul Dirac y Richard Feynman intentaron introducir una formulación de la teoría cuántica en que interviniese la acción utilizando la formulación lagrangiana de la mecánica clásica. De esa formulación sale la regla sobre los ángulos de los relojes o la interpretación de suma de todos los caminos posibles. En 1941, Feynman derivó la ecuación de Schrödinger de un principio de acción utilizando el formalismo de Dirac.
Definición de la magnitud física llamada acción como la integral temporal del lagrangiano
Formulación de la integral de camino o de suma de historias de la mecánica cuántica propuesta por Richard Feynman. En la exponencial compleja está incluida el giro o fase de la flecha y la función de onda es la amplitud de la flecha. La integral es la suma de flechas
Principio de Incertidumbre de Heisenberg (1927)
En 1926 Schrödinger creía que su ecuación para φ(t) daba una representación visual de lo que sucedía en el interior de los átomos. Creía que φ(t) estaba relacionada con la distribución de carga eléctrica dentro del átomo. Esto hasta que Max Born introdujo su interpretación probabilística.
En 1927 Heisenberg publica un artículo donde propone que solo tiene sentido hablar de la posición de una partícula si se especifica cómo se mide. Porque el acto de medir introduce una perturbación, y por ello existe un límite de la precisión con la que podemos medir simultáneamente la posición y el momento de una partícula.
La idea de este principio sería la siguiente. Partimos de una única partícula cuya posición no se conoce con precisión. Su posición vendría dada por una nube de relojes que forman su función de onda. Supondremos que esta nube es suficientemente grande y que la distancia X a la que queremos transportar todos los relojes es grande, con lo que la aguja del reloj dará muchas vueltas. Tras estos giros y contracciones de cada reloj para transportarlo a X, habrá que sumarlos todos y hacer el módulo al cuadrado del reloj resultante en X.
Si el giro del reloj es un número completo de vueltas, estos están en fase y dan un reloj más grande con la manecilla marcando las 12 en punto (en fase). Si el reloj da un número de vueltas completo más media, está en contrafase y disminuye el módulo en X.
Por tanto, si la nube es suficientemente grande y X está los suficientemente alejado, la Prob(X) tiende a 0. Es como si la partícula no se moviera. Esta cancelación de relojes podemos llamarla "orgía de interferencia cuántica". Para que se produzca esta cancelación, X debe estar alejado para que las manecillas den más de una vuelta. Sino no podrían cancelarse entre sí tan efectivamente. Si la distancia X fuera lo suficientemente pequeña para que todos los relojes marcaran en X entre la 1 y las 3 en punto, entonces todos ellos sumarían y no se cancelarían, dando un reloj más grande que marque las 2 en punto aproximadamente. Es decir hay una probabilidad de encontrar la partícula en puntos próximos razonable, aunque exteriores a la nube inicial (próximo quiere decir a menos de una vuelta de reloj).
Sabemos que la magnitud del giro de los relojes es proporcional a Ldt. La constante de Planck nos dirá qué es una nube lo suficientemente grande y que es un punto lo suficientemente alejado. Es una constante de la naturaleza que determina la escala.
Breve historia de la constante de Planck
En 1900 Max Planck encuentra la fórmula matemática para la distribución de la longitud de onda de la luz emitida por objetos calientes en función de su temperatura. Esto solucionaba el problema del cuerpo negro, que son objetos ideales que absorben y reemiten toda la radiación que reciben. Planck descubrió que podía explicar la radiación del cuerpo negro solo si suponía que la luz emitida estaba compuesta de un gran número de pequeños paquetes de energía. Esto implicaba que la energía estaba cuantizada en unidades de una nueva constante fundamental de la naturaleza: h. Siendo la energía E=hcλ-1.
La energía solo puede radiarse de manera discreta o discontinua en paquetes o cuantos cuya energía es proporcional a la frecuencia
En 1905 Einstein propone que la cuantización de la energía de la luz se debe a que la propia luz está compuesta de partículas. La luz es un flujo de fotones. Ese año Einstein también propone la Relatividad Especial y la ecuación de equivalencia entre masa y energía.
La constante de Planck h es una unidad de acción, con las mismas unidades que Ldt. Su valor 6,626 10-34 [Kgm2s-1] es minúsculo a escala macroscópica. Por ello en la vida cotidiana no notamos los efectos cuánticos. Incorporando h, el giro de las manecillas del reloj es Ldth-1. En el caso de un grano de arena de masa 1 Kg, x=1μm y t=1s, su reloj giraría 1012 veces. Existe cancelación de relojes con lo que el grano de arena está en reposo a esa escala. Pero no nos interesa este caso, sino aquel en que los relojes no se cancelan entre sí, es decir, cuando los relojes giran menos de 1 vuelta con lo que no hay orgía de interferencia cuántica. Para que haya cierta probabilidad de encontrar a la partícula en un punto a una distancia x, no debe haber orgía de interferencia cuántica. Al realizar los cálculos se obtiene que cuanto mayor es el tiempo y menores la distancia a recorrer y la masa, mayor es la probabilidad de encontrar a la partícula lejos de su posición inicial.
<1 .="" br="">
Mientras más pequeña es la región en que intentamos confinar una partícula, más lejos tiende a saltar. El Principio de Indeterminación surge de las reglas sobre el giro y tamaño de las manecillas de los relojes y sobre su suma. Es consecuencia de la proposición que una partícula puede encontrarse en cualquier lugar del universo un instante después de medir su posición. La orgía de interferencia cuántica introduce cierta moderación, y el principio de incertidumbre es lo que queda de la anarquía inicial. También es consecuencia de que la partícula va por todos los caminos posibles. Por ejemplo, la probabilidad de que un grano de arena salga del espacio equivalente a una caja de cerillas es de 6·1013 años. Sin embargo, parece que para los objetos grandes el movimiento es indetectable. Pero las cosas grandes sí se mueven y la teoría cuántica es una teoría de todas las cosas grandes y pequeñas. ¿Cómo podemos explicar el movimiento?
5. El Movimiento como una ilusión
Supongamos ahora cinco relojes, separados una distancia d, que marcan horas diferentes pero siguiendo un patrón de desfase entre ellos, es decir, formando un paquete de ondas. Si escogemos de forma apropiada la distancia x, todos los relojes de la nube se suman constructivamente en el punto X. Igual sucederá en todos los puntos entre x y x+4d. Fuera de este rango los relojes sufrirán la orgía de interferencia cuántica. Como resultado la nube de relojes se mueve. El paquete de ondas se va moviendo sin perder su forma porque los relojes que lo forman mantienen sus diferencias de hora o fase.
Si la partícula tiene una longitud de onda asociada concreta, entonces habrá movimiento. La onda de probabilidad tiene una longitud de onda concreta, y esta longitud de onda es una representación de la partícula en movimiento. ¿A qué distancia tiene que estar X para que la nube de relojes se sume constructivamente? La respuesta viene dada por la ecuación de De Broglie p=hλ-1 de 1923 y es importante porque:
- Asigna una longitud de onda a una partícula con momento conocido.
- Expresa una relación profunda entre magnitudes de partículas como el momento p, y de ondas, como la longitud de onda λ.
- Expresa una dualidad onda-partícula.
- Fue un catalizador para la mecánica ondulatoria de Schrödinger.
- Si la longitud de onda disminuye, hay que aumentar x, con lo que v también aumenta.
Paquetes de Ondas
El principio de incertidumbre hace que el paquete de ondas se esparza al desplazarse. Si esperamos el tiempo suficiente, el paquete de ondas se desintegrará y no podremos predecir donde se encuentra la partícula. Esto tendrá consecuencias para cualquier intento de medir su velocidad. Si esperamos un tiempo t mayor para reducir la incertidumbre lo que sucede es que el paquete se desperdiga. Una partícula de momento definido implica que su incertidumbre en la posición tiende a infinito.
Un pequeño paquete de ondas está formado por muchas ondas infinitamente largas de longitud de onda entre 0 y d. Cuantas más ondas de longitudes de onda diferentes se sumen, más estrecho puede llegar a ser el paquete. Podemos pensar que una partícula está descrita por una superposición de relojes en cada punto, uno por cada valor posible del momento. La orgía de interferencia cuántica necesita varias longitudes de onda y, por tanto, varios momentos. Con solo un momento, una longitud de onda, no hay orgía de interferencia cuántica y no es posible localizar a la partícula (la anchura del paquete de ondas tiende a infinito).
Hasta ahora una partícula es representada por una función de onda que en cada punto del espacio da una probabilidad de encontrar la partícula. Es decir, tenemos una función de onda en el espacio de posiciones. Pero una partícula también puede representarse por una suma de senoides de longitud de onda λ, una por cada momento posible de la partícula. Al sumar todas las senoides obtenemos una función de onda espacial. Además, cada senoide puede representarse con un único reloj, con lo que hay una representación alternativa: una nube de relojes, uno por cada valor posible del momento. Lo que representan son los valores probables por cada momento (altura de cada senoide), generando una función de onda en el espacio de momentos. Cada senoide es un estado propio del momento.
Una partícula de momento definido implica infinitos relojes en el espacio de posiciones y un reloj en el espacio de momentos. Una partícula con posición definida supone un reloj en el espacio de posiciones e infinitos relojes en el espacio de momentos.
Con la ecuación de De Broglie que vincula el momento y la longitud de onda se puede llegar también al principio de incertidumbre. El movimiento de los objetos de un punto a otro es una ilusión. Las partículas se mueven caóticamente gobernadas por el principio de incertidumbre. Es más acertado suponer que todas las partículas van de A a B por todos los caminos posibles y cuando sumamos todas las posibilidades (todos los relojes resultantes en X) surge el movimiento como nosotros lo percibimos.
6. La música de los átomos
Los átomos son inmensos y vacíos, lo que significa que los objetos a escala real son inmensos y vacíos. ¿Qué sucede exactamente en el interior de un átomo? ¿Cómo afecta la teoría cuántica al mundo cotidiano? Entender la estructura de los átomos es necesario para entender el universo en su conjunto.
Electrón en una caja
La mecánica ondulatoria es más apropiada que la adición de relojes. Cualquier perturbación se puede describir mediante una combinación de ondas estacionarias. Las ondas estacionarias son claves para entender la estructura de los átomos. Surgen cuando se confina una perturbación periódica. Las características del espacio físico determinan las longitudes de onda permitidas. La longitud de onda mayor es el armónico fundamental. Normalmente también están otros armónicos, que son múltiplos del principal. Al existir longitudes de onda concretas, se dice que estas están cuantizadas.
En una onda estacionaria su forma no varía con el tiempo, solo su amplitud. Los picos y los nodos siempre están en el mismo sitio. En el caso del electrón, su estado general estará descrito por una combinación de ondas estacionarias. Si el electrón está confinado en un potencial cuadrado de anchura L, la función de onda debe anularse en los bordes, con lo que λN=2L. Como p=hλ-1, el momento también está cuantizado. Este es un caso especial de ondas estacionarias cuánticas sinusoidales. En el caso de un tambor, la frontera es circular con lo que las ondas estacionarias son funciones de Bessel. En el caso del electrón atrapado por un protón, las ondas estacionarias tampoco son senoides, por lo que se pierde la relación sencilla entra longitud de onda y momento. Pero si el momento está cuantizado, también lo está su energía. Si E=½mv2 y p=mv, entonces la energía es E=p2(2m)-1.
Para potenciales más complejos, cada onda estacionaria siempre corresponde a una partícula con energía bien definida. El movimiento del electrón puede variar, pero su energía permanece constante.
En una onda estacionaria los picos y los nodos están siempre en el mismo lugar. Por tanto los relojes en cada posición tienen siempre la misma amplitud. Solo varía su fase y además de forma coordinada. Las ondas estacionarias de alta frecuencia son aquellas en que la fase de cada punto gira más rápido. Pero a diferencia de una senoide, una onda estacionaria no tiene una única longitud de onda definida. Por tanto, ¿qué significa que un electrón tiene una longitud de onda determinada? Los estados de un electrón están cuantizados y permanece en uno de ellos indefinidamente si nada externo ocurre. La ley de la conservación de la energía exige que esta energía no cambie espontáneamente sin motivo. Por tanto las ondas estacionarias son apropiadas para definir un electrón de energía definida. Si la longitud de onda disminuye, la frecuencia aumenta y también lo hace el momento y la energía, con lo que más rápido varía la fase de los relojes.
La mínima energía de un electrón se corresponde con la onda estacionaria fundamental y con el nivel de energía fundamental. Las ondas estacionarias con frecuencia más elevadas se corresponden con estados excitados.
El electrón puede describirse mediante la composición de muchas ondas estacionarias, con lo que no tendrá una única energía. Una medición de la energía del electrón debe dar una de los asociadas con una de las ondas estacionarias componentes. Para calcular la probabilidad de que un electrón tenga una energía determinada hay que tomar los relojes asociados a una onda estacionaria, elevarlos al cuadrado y sumarlos. La suma de todas las probabilidades (una por cada onda estacionaria) es igual a la unidad. Como la energía está cuantizada los electrones no irradian energía continuamente mientras caen al núcleo porque no pueden perder energía poco a poco. Esto se puede relacionar con el espectro de emisión de los átomos, concretamente con el del hidrógeno y las ondas cuánticas que encajan en él.
La energía del fotón es Efotón=cp=hclambda-1 con lo que los fotones tienen longitudes de onda y energías específicas creando el espectro de emisión de un átomo. Cada línea del espectro es una frecuencia asociada a una longitud de onda del fotón que cae de un estado excitado al normal. Esto demuestra que es apropiado expresar estados de los electrones en función de valores permitidos de energía. Podemos precisar algo más sobre las energías permitidas de los electrones mejorando el modelo cambiándolo del potencial cuadrado a un potencial de Coulomb de un protón de simetría esférica. En este caso las ondas estacionarias no son senoides, con lo que no hay estados de momento definido pero estos si se corresponden a estados de energía bien definidos.
Para entender cómo se crea el potencial hay que añadir nuevas reglas según las que una partícula puede emitir o absorber otra partícula. Una interacción entre dos partículas consiste en la emisión o absorción de otra partícula. En el caso de las líneas espectrales, un electrón emite un fotón que es una línea espectral (espectro de emisión), o bien absorbe energía y pasa a un nivel excitado (espectro de absorción). Nos queda la pregunta, ¿Por qué no atravesamos el suelo? ¿Por qué la materia es rígida si es casi vacía?¿Por qué no se puede comprimir hasta el límite? La respuesta es el principio de exclusión de Pauli.
7. El Universo en la Cabeza de un Alfiler
De momento los experimentos no exigen que las partículas no puedan ser objetos puntuales, aunque el hecho de una carga finita comprimida en un espacio infinitamente pequeño es espinoso. Quizás el desarrollo de una teoría cuántica de la gravedad apunte a una extensión no nula de las partículas. Esto permite imaginar el universo en la cabeza de un alfiler.
En 1967 se demostró que la materia solo puede ser estable (y no hundirse sobre sí misma) si los electrones cumplen el principio de exclusión de Pauli.
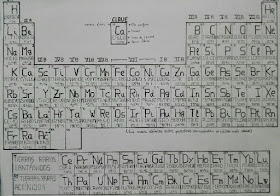
En 1 dimensión, existe un número cuántico, el nivel de energía n (n = 1, 2, 3, ... )
En 3 dimensiones, existen tres números cuánticos. Para los tres primeros valores de n (1, 2 y 3) hay 1, 4 y 9 niveles de energía permitidos respectivamente debido a todas las posibles comvinaciones de los tres números cuánticos. En la tabla periódica, si dividimos por dos los elementos de las primeras cuatro filas obtenemos 1, 4, 4 y 9. Los elementos se ordenan según el número de protones, que es igual al número de electrones. Este orden tiene que ver con electrones y sus energías permitidas.
La tabla periódica de los elementos
Los átomos tienden a compartir electrones para tener sus niveles de energía llenos, y así estar en configuraciones de mínima energía. ¿Por qué solo dos electrones en cada nivel de energía? Por el principio de exclusión de Pauli: "Dos electrones en un átomo no pueden compartir los mismos números cuánticos". Para ello introdujo un nuevo número cuántico: el espín. El espín es una propiedad del electrón relacionada con su comportamiento bajo un campo magnético externo. Pero su verdadero origen es una consecuencia directa y sutil de la teoría de la relatividad especial que solo se comprendió cuando Dirac escribió en 1928 la ecuación que describía el comportamiento cuántico del electrón.
El principio de exclusión implica una nueva "regla de relojes:" Debemos asociar un único reloj a cada manera en que un proceso entero puede suceder". Esta regla es necesaria cuando contemplamos más de una partícula.
En un sistema de muchas partículas idénticas, para determinar la probabilidad de que estas se encuentren en un conjunto determinado de posiciones debemos combinar todos los relojes asociados a cada una de las maneras distintas en las que las partículas pueden alcanzar esas posiciones. Solo hay dos maneras de combinarlos, dos únicas opciones:
- sumarlos sin giro previo (giro de cero grados).
- sumarlos con giro previo de 180 grados (no da el mismo reloj pero sí la misma probabilidad)
Solo hay dos maneras porque las partículas son indistinguibles y estas son las únicas maneras de juguetear con giros y contracciones de los relojes antes de sumarlos que permitan obtener un reloj final que no dependa sobre cuál de los dos relojes se apliquen los cambios. Si tenemos dos electrones con sus relojes asociados y queremos combinarlos, si fueran distinguibles los sumaríamos. Pero como no lo son, la probabilidad del suceso total no debe variar si intercambio las etiquetas. Por tanto no puedo modificar el tamaño de los relojes. Sí que puedo modificar la fase si ello no modifica la probabilidad resultante tras la combinación. La naturaleza utiliza ambas opciones posibles en lo que se conoce como el teorema de la estadística del espín:
- Los electrones implican un giro previo de su reloj antes de sumar. Por ello son fermiones (se comportan según la estadística de Fermi-Dirac) y tienen espín semientero.
- Los fotones o los bosones de Higgs no implican un giro previo. Son bosones (se comportan según la estadística de Bose-Einstein) y tienen espín entero.
El espín es una medida del momento angular de una partícula:
- Los fermiones tienen espín ½ o -½.
- El fotón tiene espín 1.
- EL bosón de Higgs tiene espín 0.
Siendo la regla general:
siendo s el espín de la partícula. Por tanto, hay 2 tipos de electrones (diferenciados por su espín), 3 tipos de fotones en función de su polarización, y un tipo de bosón de Higgs.
n = 2s + 1
siendo s el espín de la partícula. Por tanto, hay 2 tipos de electrones (diferenciados por su espín), 3 tipos de fotones en función de su polarización, y un tipo de bosón de Higgs.
El teorema de la estadística del espín surge cuando la teoría cuántica se formula de manera que sea compatible con la teoría de la relatividad especial (teoría cuántica de campos).
Este giro previo es la razón del principio de exclusión de Pauli y, por lo tanto, de la estructura y la estabilidad de la materia. Hace que la probabilidad de encontrar dos electrones en el mismo punto sea nula.
8. Interconectados
Imaginemos dos átomos de Hidrógeno muy alejados. Aunque estén muy lejos, podría ser que un instante después, los electrones se intercambiaran. Todo lo que puede suceder, sucede. Además, aunque estén muy alejados, sus funciones de onda se solapan y por tanto no pueden tener los mismos números cuánticos. Podríamos pensar que el estado de mínima energía del sistema fuera dos átomos de hidrógeno aislados con sus electrones en niveles de energía mínima, pero eso no es posible.
Por tanto, hay tantos estados de energía como átomos, todos ellos muy parecidos, y más similares mientras más alejados estén los átomos. Como la función de onda del electrón es infinita, es como si estuvieran todos los electrones interconectados porque el principio de exclusión les obliga a saber cómo están el resto de los electrones para encontrar su nivel de energía. Esto es porque todos los protones de todos los átomos contribuyen a crear un pozo de potencial global. En cambio, si los pozos fueran muy profundos o estuvieran muy separados, las energías permitidas deberían parecerse mucho a las de un electrón aislado y su función de onda sería una senoide.
Las energías de los dos electrones no pueden ser las mismas porque tiene que haber una probabilidad, por muy alejados que estén y profundos que sean los pozos, que el electrón salte de un átomo a otro. Y si la energía es la misma, el electrón no se mueve del átomo.
Los estados de energía bien definida se corresponden con ondas estacionarias. Y en estos casos, la onda de probabilidad debería variar con el tiempo para permitir que el electrón cambie de posición.
Para que se cumpla el principio de exclusión las ondas de probabilidad no pueden ser exactamente iguales, por eso un electrón tiene una función de onda simétrica y el otro electrón una función de onda antisimétrica.
Si los pozos son suficientemente profundos o están suficientemente alejados, las dos energías serán muy similares y casi iguales a la energía más baja de una partícula confinada en un solo pozo aislado. Lo que las hace diferentes es la parte entre ambos pozos, siendo la función de onda simétrica la de menor energía.
En el fondo la función de onda de cada electrón en un sistema de dos electrones (como un átomo de helio) es la superposición de dos funciones de onda de menor energía. Un electrón no posee una única energía, sino dos energías posibles, la asociada a cada función de onda. El electrón se encuentra en dos estados al mismo tiempo. Como los dos estados de esta superposición no tienen exactamente la misma energía, con el paso del tiempo sus relojes giran a ritmos diferentes similar al caso en que dos ondas de frecuencia similar se suman cuando están en fase o casi se cancelan cuando están en contrafase (pulsos).
A medida que acercamos los pozos aumenta la probabilidad de que el electrón se encuentre en la región entre ambos protones.
En el caso de 3 átomos, existen 3 pozos de potencial y por tanto tres niveles de energía mínima para cumplir el principio de exclusión de Pauli. En el caso de N pozos (N átomos), obtenemos N energías diferentes para cada estado del sistema, de forma que estas N energías forman un continuo o bandas continuas. Estas bandas explican porque algunos materiales (metales) conducen la electricidad, mientras que otros (aislantes) no.
Si tenemos N átomos de hidrógeno, la banda del primer nivel de energía está medio llena. En el caso del helio, está llena. En el caso del litio, la primera capa está llena y la segunda medio llena. Las bandas llenas o medio llenas hacen que los materiales sean conductores o aislantes.
Si conectamos esta cadena de átomos a una batería de bajo voltaje, el electrón en el nivel más bajo está bloqueado porque los niveles superiores están también bloqueados por el principio de exclusión de Pauli. Por ello no consigue suficiente energía para ir al primer nivel libre. En el caso de electrones de niveles superiores, se podría absorber esta energía pero solo si no están exactamente en el nivel más alto de una banda llena (número impar de electrones). Entre bandas de energía, el salto de energía es grande. El caso de banda de energía llena es el de un material aislante. El de una banda de energía no llena, como el flujo de energía es constante, los electrones van saltando progresivamente a bandas superiores generando una corriente, resultando en un material conductor.
Podríamos pensar que un electrón puede ir saltando progresivamente por un nivel de energía a medida que recibe energía de una batería. Pero esto choca con la ley de Ohm, que dice que la corriente es constante para un potencial concreto (V=RI). Esto se debe a que debido a impurezas en la red de átomos (no perfectamente ordenados) y a su agitación térmica. Los electrones van subiendo y bajando y en promedio resulta la ley de Ohm con la resistencia como medida de la impureza del material. Además, realmente es la agitación de los núcleos la que hace que los electrones salten de la banda de valencia (la llena) a la de conducción. Si la brecha entre la banda de valencia y la de conducción es suficientemente pequeña, la agitación del núcleo puede empujar a un electrón a la banda de conducción e iniciar la corriente eléctrica. En los materiales con un número suficiente de electrones que pueden saltar de la banda de valencia a la de conducción son los semiconductores. Ejemplos de estos son el silicio o el germanio (calientes conducen, fríos aíslan).
9. El mundo moderno
El primer ordenador con transistores se fabricó en Manchester en 1953 (92 transistores). El transistor es sin duda la aplicación más importante de la teoría cuántica. En un semiconductor la corriente la transportan o bien los electrones de la banda de conducción o bien los electrones de la banda de valencia (huecos). En este último caso, si hay energía disponible de una batería, los huecos son llenados por electrones que a su vez dejan huecos detrás. Hay corriente de huecos. El salto de los electrones a la banda de conducción se produce por agitación térmica o por la energía de una batería.
Circuito electrónico basado en dos transistores bipolares BJT (bipolar junction transistor)
En un semiconductor se produce una corriente de electrones en un sentido y una corriente de huecos en sentido contrario que se suman en una única corriente neta de electrones. Es una corriente controlable con un poco de ingenio técnico. En el caso de un conductor, la corriente está dominada por el gran número de electrones en la banda de conducción, siendo la corriente adicional de los pares electrón-hueco inapreciable. Para controlar mejor la corriente en un semiconductor, se dopa para crear nuevos niveles de energía al alcance de los electrones.
Un semiconductor de tipo n es silicio dopado con átomos de fósforo, que tiene un electrón más en la capa de valencia que el silicio, que además es poco atraído por el núcleo. A temperatura ambiente salta fácilmente a la banda de conducción. El número de átomos de fósforo indica la corriente que se puede generar. Entre la capa de conducción y la de valencia se crea una tercera capa intermedia, llamada nivel donante de electrones, con los electrones procedentes del fósforo.
Un semiconductor de tipo p es silicio dopado con átomos de aluminio, que tiene un electrón menos en la capa de valencia que el silicio. Por ello aparecen huecos. Un electrón del silicio puede saltar fácilmente al nivel de energía de los huecos creado por los átomos de aluminio (cercano a la banda de valencia). Este nuevo nivel se llama nivel aceptor de electrones.
Si juntamos una región p y otra n y aplicamos un potencial entre ambas tenemos un volumen de electrones y huecos (los de las capas intermedias) listos para generar una corriente. Es el resultado de un equilibrio por el potencial entre la capa p y la capa n existentes sin batería externa. Al aumentar el potencial la corriente solo puede fluir de p a n. Este es el caso de un diodo. Si juntamos dos regiones n separadas por una región p creamos un transistor. Lo interesante sucede cuando aplicamos un potencial a una región n y a la región p. Si Vc es mayor que Vb se produce una cascada de electrones entre las regiones n (corriente de colector). Si Vb es cero, los electrones en cada región n están en equilibrio. Si Vb es mayor que un umbral, se crea un corredor de huecos por el que pasaran los electrones de una región n a la otra.
Con dos transistores se puede crear una puerta lógica (negación o NOR). Con 4 transistores, se pueden crear las puertas lógicas AND y OR. Y con las puertas lógicas se crean los procesadores.
10. Interacción
Hasta ahora hemos obviado las interacciones usando el concepto de potencial sin explicar su origen. A las reglas de como saltan las partículas hay que añadir el conjunto de reglas que explican cómo interactúan entre sí que proporciona la teoría cuántica de campos, la primera de las cuales es la electrodinámica cuántica o QED por sus siglas en inglés.
Lagrangiana de la Electrodinámica Cuántica, la teoría que describe como interacciona la luz con la materia. M es la masa del electrón, A es el potencial vector del electromagnetismo y F es el tensor electromagnético. Los dos primeros corresponden a la ecuación de Dirac, el tercero es el de interacción entre el electrón y el fotón (consecuencia de la simetría gauge) y el cuarto es el de la propagación del fotón en ausencia de fuentes (onda electromagnética)
El origen de la QED está en la cuantización del campo electromagnético de Maxwell por Dirac en los años 20. La QED explica:
¿Cómo emite un electrón un fotón cuando se mueve entre los niveles de energía de un átomo?
¿Qué le sucede al fotón cuando es absorbido por un electrón?
¿Cómo las partículas con carga eléctrica interactúan entre sí y con las partículas de luz (fotones)?
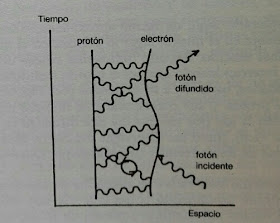
La teoría cuántica antigua no explicaba por ejemplo el efecto Lamb, un ligero desplazamiento de los niveles de energía del hidrógeno debido a la emisión y absorción de fotones virtuales.
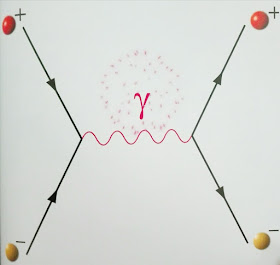
Diagrama de Feynman en que un electrón y un positrón se aniquilan en fotones virtuales que a su vez se desintegra en un par electrón-positrón
La QED lo explica todo salvo la gravedad y los fenómenos nucleares. Es decir, explica la materia, la luz, la electricidad y el magnetismo.
Los diagramas de Feynman permiten calcular las probabilidades más fácilmente, como la de encontrar dos electrones en X e Y tras un tiempo T. Cada diagrama es una interacción posible con un reloj cuántico o flecha asociado. Para llegar de un punto a otro los electrones no siguen una única trayectoria, sino que se dispersan mutuamente de todas las maneras posibles. Los electrones pueden intercambiar fotones o emitir un fotón y reabsorberlo ellos mismos. Pero siempre cumpliendo dos reglas:
- Los electrones solo pueden saltar de un lugar a otro.
- Los electrones solo pueden emitir o absorber un único fotón.
Es decir, los electrones solo pueden saltar o desintegrarse.
Cuando un electrón emite o absorbe un fotón hay que introducir un factor de contracción g. Si en un proceso se produce una emisión y una absorción, entonces el factor es g2. Este factor está relacionado con la intensidad de la fuerza electromagnética y la constante de estructura fina α=g2 dividido ente 4π. Para acabar el cálculo hay que considerar todas las maneras de llevar los electrones a X e Y y para todos los puntos en que un electrón puede emitir un fotón y todos los puntos en que el otro electrón puede absorberlo.
Antimateria
La QED permite a las partículas viajar hacia adelante y hacia atrás en el tiempo. Esto parece violar la ley de la causalidad pero puede interpretarse como una antipartícula viajando hacia adelante en el tiempo.
Las antipartículas fueron introducidas por Dirac en 1931 para explicar la existencia de partículas con energía negativa.
La teoría cuántica de campos es el nombre de la estructura matemática más profunda en la que se basan las reglas sobre los saltos y las desintegraciones, y destaca por ser la única teoría posible de las partículas diminutas que también respeta la relatividad especial. El aparato teórico de la teoría cuántica de campos obliga a fijar las reglas sobre saltos y desintegraciones, perdiendo la libertad de elegir otras nuevas.
Se utilizan simetrías para eliminar opciones, con lo que parece que el universo deba ser como es. Por ejemplo, la relatividad impone simetrías a la estructura del espacio-tiempo.
Finalmente el efecto Lamb no puede explicarse con la teoría cuántica de Heisenberg y Schrödinger. Solo los cálculos que consideran efectos de segundo orden como creaciones de parejas electrón-positrón como consecuencia de un fotón predicen correctamente los niveles de energía del átomo de hidrógeno.
El efecto Lamb fue el primer caso explicado con las fluctuaciones cuánticas. Actualmente la QED es la precursora de las teorías cuánticas de campos, es modelo de las teorías de las interacciones fuerte y débil.
11. El espacio vacío no está tan vacío
La QED no explica:
- Los procesos debidos a la fuerza nuclear fuerte que mantienen unidos a los quarks en protones y neutrones.
- Procesos relacionados con la fuerza nuclear débil, responsable de la fusión nuclear.
Ambas fuerzas están descritas por la misma aproximación basada en Teoría Cuántica de Campos que la descrita para la QED. La teoría de estas 3 fuerzas en su conjunto se conoce como Modelo Estándar.
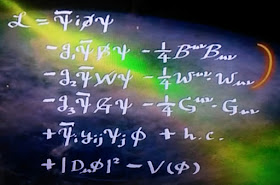
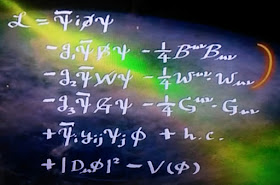
Lagrangiana del modelo estándar a partir de la cual pueden explicarse todos los fenómenos salvo los relacionados con la gravedad
Formulación de la integral de camino o de suma de historias de la mecánica cuántica propuesta por Richard Feynman. En la exponencial compleja está incluida la lagrangiana del modelo estándar y la de la relatividad general (para campos gravitatorios débiles)
Modelo Estándar
Las partículas conocidas se dividen en quarks (6 sabores agrupados en 3 familias cada uno de tres posibles colores), leptones (3 electrones y 3 neutrinos agrupados también en tres familias). Estas partículas forman la materia ordinaria conocida. Además tenemos los bosones mediadores de fuerzas como los fotones, gluones y los bosones gauge débiles W+- y Z. No sabemos porque son estas partículas las que son ni por qué las reglas son las que son. Estas reglas son una consecuencia de los principios de las teorías cuánticas de campos y de la simetría gauge.
Las partículas elementales del Modelo Estándar se agrupan en 3 familias. En esta imagen cada familia corresponde a las partículas de las primeras dos columnas de la izquierda, las dos columnas centrales y las dos columnas de la derecha
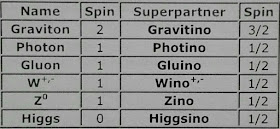
Otras posibles partículas relacionadas con la materia oscura serían:
- Partículas supersimétricas.
- Excitaciones o modos de Kaluza-Klein características de dimensiones extra.
Los bosones y sus posibles compañeras supersimétricas
Los fermiones, las partículas que constituyen la materia, y sus posibles supercompañeras
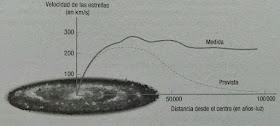
La materia visible se insuficiente para explicar el movimiento de las estrellas periféricas de las galaxias y requeriría de un nuevo tipo de materia para ser explicado
Las principales diferencias entre las descripciones cuánticas de las distintas fuerzas tienen que ver con las reglas de desintegración. Con estas nuevas reglas podremos dibujar diagramas de Feynman y nos permitirán calcular la probabilidad de que se produzca algún suceso. Algunas de estas nuevas reglas son:
- Diagramas de Feynman de interacción de electrones con bosones gauge débiles W y Z.
- Diagramas de Feynman de interacción de quarks u y d con bosones gauge débiles W (importante para la fusión nuclear).
- Diagramas de Feynman de interacción entre gluones.
La fusión nuclear es posible no por la teoría del Sol, sino por la transformación de un quark up en un quark down debido a la fuerza nuclear débil. Entonces un protón se convierte en un neutrón, este se puede acercar al protón para crear un deuterón, que a su vez genera helio fácilmente.
Según el Modelo del Big Bang, los primeros átomos de Hidrógeno y Helio se crearon mediante reacciones de fusión nuclear gracias a las elevadas temperaturas
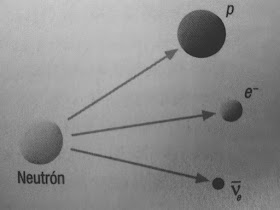
La fuerza nuclear débil es la responsable de la desintegración beta en la que un neutrón se transforma en un protón más un electrón más un antineutrino
Diagrama de Feynman de la desintegración beta en la que un bosón W se lleva una unidad negativa de carga y se acaba desintegrando en un electrón y un antineutrino.
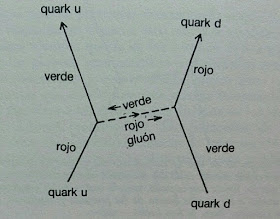
Respecto a la fuerza nuclear fuerte se cumple:
- Solo los quarks pueden descomponerse en gluones (además es lo más probable que suceda). Por eso es una fuerza nuclear fuerte.
- Tiene un alcance corto porque los gluones se desintegran rápidamente al interactuar con otros gluones. Los fotones alcanzan largas distancias porque no interactúan entre sí.
Los hadrones formados por tres quarks se llaman bariones y los mesones son partículas formadas por un quark y un antiquark
El origen de la masa
En las teorías cuánticas de campos las partículas pueden desintegrarse o saltar de un punto a otro. ¿Cuál es pues el origen de la masa? La explicación actual radica en el mecanismo de Higgs y el bosón de Higgs.
Las reglas de salto para el fotón y el electrón son diferentes. Los motivos son:
- Hay dos tipos de electrones (espín ½ o -½) y tres tipos de fotones (o polarizaciones).
- El electrón tiene masa y el fotón no. Este es el motivo crucial.
Las partículas se mueven por todos las caminos posibles, el directo y mediante zigzagueos (y contracciones que son proporcionales al inverso de la masa). Si la masa es nula, la contracción es infinita con lo que el zigzagueo es imposible, quedando solo el camino directo (regla de salto de partículas con masa nula). La cantidad de zigzagueo es lo que interpretamos como masa.
La interacción con el bosón de Higgs origina el zigzagueo y la aparición de la masa. El fotón no tiene ninguna regla de desintegración que lo acople a las partículas de Higgs, por ello no interactúan con él y no tienen masa.
La mecánica cuántica con el principio de incertidumbre afirma que no existe el espacio vacío porque entonces la energía sería definida y precisa, sino un frenesí de creación de partículas y antipartículas dentro de lo permitido por el principio de incertidumbre. Por eso no es extraño suponer que el espacio vacío pueda estar impregnado de bosones de Higgs.
Las partículas de Higgs surgieron de una transición de fase que se produjo muy poco tiempo después del Big Bang al reducirse la energía por debajo de un umbral.
Cuando el Universo se enfrió, un vacío sin bosones de Higgs era una configuración energéticamente menos favorable que un vacío lleno de partículas de Higgs, que era el estado natural.
A la izquierda el potencial de Higgs es nulo cuando el campo de Higgs también lo es. Sin embargo a la derecha se rompe esta simetría y el potencial es diferente de cero cuando el campo de Higgs es nulo
En el caso de protones y neutrones el mecanismo de Higgs es poco importante porque su masa es fundamentalmente la energía de los gluones y pares quarks-antiquarks. Sin embargo, es importante para explicar el origen de la masa de los bosones gauge débiles W y Z.