1. Prólogo
Este libro, El Sueño de una Teoría Final escrito por el premio Nobel de física Steven Weinberg está dividido en tres partes:
- Los capítulos del 1 al 3 presentan la idea de una teoría final.
- Los capítulos del 4 al 8 explican cómo hemos sido capaces de progresar hacia una teoría final.
- Los capítulos del 9 al 11 pretenden especular sobre la forma de una teoría final y en que medida su descubrimiento afectará a la humanidad.
En el siglo XX la física avanzó mucho con la teoría de la relatividad, que cambió nuestra idea del espacio y del tiempo, y de la gravitación, y con la mecánica cuántica. Está última ha transformado el propio lenguaje que utilizamos para describir la naturaleza: en lugar de partículas con posiciones y velocidades definidas hablamos de funciones de onda y probabilidades.
De la fusión de la relatividad y la mecánica cuántica la materia ha perdido su papel central en favor de los principios de simetría. Sobre esta base hemos construido una teoría satisfactoria sobre el electromagnetismo y de las interacciones débil y fuerte entre las partículas elementales.
El sueño de una teoría final no empezó en el siglo XX. Un siglo antes del nacimiento de Sócrates, en la Escuela de Mileto, los milesios liderados por Tales buscaban explicaciones de los fenómenos naturales en términos de un constituyente fundamental de la materia. Para Tales esta substancia fundamental era el agua. Para Anaxímenes, el último de esta escuela, era el aire.
Un siglo después, en Abdera, en la costa de Tracia, Demócrito y Leucipo enseñaban que toda la materia está compuesta de minúsculas partículas eternas que ellos llamaron átomos.
Sin embargo ninguno de los presocráticos no consideraban necesario la comprensión y predicción cuantitativa de los fenómenos. Por tanto sus explicaciones no eran científicas al no poderse comprobar experimentalmente. Desde este punto de vista, la física de Aristóteles en sus obras Física y Sobre el Cielo no era mejor.
Aunque la comprensión cuantitativa no era su objetivo, el razonamiento cuantitativo exacto no fue desconocido en el mundo antiguo. Durante milenios los pueblos han conocido las reglas de la aritmética y de la geometría plana y las grandes periodicidades del Sol, la Luna y las estrellas, incluyendo sutilezas como la precisión de los equinoccios. Además de esto hubo un florecimiento de la ciencia matemática después de Aristóteles durante la era helenística. Con Arquímedes en Siracusa y Eratóstenes en Alejandría. Nada semejante se había visto hasta la aparición de la ciencia moderna en Europa en el siglo XVII con Galileo y su método científico además de sus descubrimientos, Kepler o Descartes.
El sueño moderno de una teoría final empezó realmente con Newton y sus leyes del movimiento y de la gravitación universal. La teoría de Newton explicaba tantas cosas que por primera vez se intuyó la posibilidad de una teoría explicativa realmente global.
Las órbitas de los planetas del Sistema Solar fueron descritas por primera vez por la Ley de Gravitación Universal
Parecía que mediante la teoría de Newton se podría predecir la posición futura de una partícula conociendo su posición y velocidad actuales. Como esto no funciona para los átomos, a medida que los científicos fueron aprendiendo más sobre química, la luz, la electricidad y el calor en los siglos XVIII y XIX, la posibilidad de una explicación según las líneas newtonianas debió parecer más y más remota. Aún así, a finales del siglo XIX existía la sensación de que todo estaba descubierto en física. Pero esto cambio a finales del siglo XIX.
Para un físico el siglo XX empieza realmente en 1895 con el descubrimiento de los rayos X por Roentgen. Esto animó a la comunidad científica y rápidamente se fueron sucediendo los descubrimientos:
- La radiactividad por Bequerel en 1896.
- El electrón por J.J. Thomson en 1897.
- La cuantización de la energía por Planck en 1900.
- La Relatividad Especial de Einstein en 1905.
- El Movimiento Browniano de Einstein en 1905.
- La Explicación del efecto fotoeléctrico.
- El modelo del átomo de Rutherford en 1911.
- El modelo de Bohr en 1913 para explicar el espectro del hidrógeno.
Experimento de Rutherford en que se lanzaban partículas alfa contra una fina lámina de oro y se observaba su trayectoria
El sueño de una teoría final unificadora empezó a tomar forma realmente por primera vez a mediados de los años 20, con el descubrimiento de la mecánica cuántica. Esta nueva teoría permitía calcular las propiedades de los átomos individuales y su interacción con la radiación además de los átomos combinados en moléculas. Finalmente quedó claro que los fenómenos químicos son lo que son debido a las interacciones eléctricas de los electrones y los núcleos atómicos.
Cuando los físicos estaban asombrados por la capacidad predictiva de la mecánica cuántica, empezaron las dificultades al aplicar esta teoría no solo a los electrones, sino también a los campos eléctrico y magnético que producen. En estos casos resultaba que la energía del átomo era infinita!
Otros infinitos aparecieron en otros cálculos y durante cuatro décadas fue el mayor obstáculo para el progreso de la física. Finalmente este problema se soluciona en teorías de cierto tipo especial, sirviendo de criba para las teorías candidatas a una teoría final.
A partir de aquí los progresos realizados hacia una teoría final han consistido en unificar el electromagnetismo con la fuerza nuclear débil en la teoría electrodébil, que se ha unificado a su vez con la fuerza nuclear fuerte en el modelo estándar.
Actualmente la teoría de supercuerdas o la Gravedad Cuántica de Bucles son las candidatas con más opciones de convertirse, o al menos formar parte, de la teoría final.
Espacio liso de la Relatividad General a la izquierda y, a la derecha, cuantos de espacio enlazados según la Gravedad Cuántica de Bucles
Pero una teoría final no será el fin de la ciencia, será final en solo un sentido: supondría un fin para cierto tipo de ciencia, la vieja búsqueda de aquellos principios que no pueden ser explicados en términos de principios más profundos.
2. Sobre un trozo de tiza
La tiza es blanca porque refleja por igual todas las longitudes de onda del espectro visible. Gracias a Einstein que en 1905 comprendió que la luz está compuesta por un haz de fotones y al modelo de Bohr propuesto en 1913 en que solo unas determinadas órbitas de energía son permitidas para los electrones podemos profundizar un poco más. La tiza es blanca porque las moléculas de las que está compuesta no tienen ningún estado para el electrón al que resulte especialmente fácil saltar absorbiendo fotones de cualquier color dentro de la luz visible.
La cuantización de la energía no se comprendió bien hasta la llegada de la mecánica cuántica, donde las partículas son descritas mediante funciones de onda cuyo modulo al cuadrado proporciona la probabilidad de encontrarla en un lugar determinado. Debido a las condiciones de contorno impuestas por la energía potencial de los núcleos de los átomos debido a su carga eléctrica, la función de onda solo puede presentarse en ciertos estados concretos asociados a una energía determinada.
La energía solo puede radiarse de manera discreta o discontinua en paquetes o cuantos cuya energía es proporcional a la frecuencia
La luz igual que los átomos solo puede existir en ciertos estados cuánticos de energía definida, igual a un número entero de veces la energía de un fotón.
La comprensión de por qué las ecuaciones de la mecánica cuántica son las que son, de por qué la materia esta formada por unas partículas determinadas y de por qué existe algo como la luz vino con el éxito del modelo estándar de partículas. Un requisito clave para ello fue la reconciliación en los años 40 de la Relatividad Especial con la mecánica cuántica. Ambas son prácticamente incompatibles y solo pueden coexistir en un tipo determinado de teorías. En estas teorías las fuerzas entre partículas solo pueden surgir del intercambio de otras partículas. Además todas estas partículas son cuantos de varios tipos de campos. Por ejemplo existe un campo electrónico cuyo cuanto es el electrón y el cuanto del campo electromagnético es el fotón. No existen campos para los protones y los neutrones porque estos están formados por otras partículas elementales: los quarks, que sí tienen campos asociados.
Las ecuaciones de una teoría de campos como el modelo estándar no tratan con partículas sino con campos: las partículas aparecen como manifestaciones o excitaciones de dichos campos.
La materia está formada por electrones, protones y neutrones sencillamente porque todas las demás partículas masivas son muy inestables a las energías normales de nuestro mundo.
Actualmente existen varias preguntas sin respuesta:
- ¿Por qué existen los campos que existen y no más o menos?
- ¿Por qué estos campos tienen las propiedades supuestas en el modelo estándar?
- ¿Por qué la naturaleza obedece los principios de la relatividad y de la mecánica cuántica?
- ¿Por qué la estructura de la materia se replica en tres generaciones de quarks y leptones?
- ¿Por qué todas las fuerzas se deben a simetrías gauge locales?
Las partículas elementales del Modelo Estándar se agrupan en 3 familias. En esta imagen cada familia corresponde a las partículas de las primeras dos columnas de la izquierda, las dos columnas centrales y las dos columnas de la derecha
A diferencia de una deducción, una explicación científica es unidireccional. La ley de Planck de la radiación térmica puede ser deducida de la teoría fotónica de la luz, pero la segunda es más fundamental y, por tanto, la radiación térmica es explicada gracias a la teoría fotónica de la luz.
Una explicación científica puede ser también algo menos que una deducción, pues podemos decir que un hecho se explica por algún principio aunque no podamos deducirlo a partir de dicho principio. Utilizando las reglas de la mecánica cuántica podemos deducir diversas propiedades de los átomos y las moléculas más sencillos e incluso estimar los niveles energéticos de moléculas complicadas, como las del carbonato cálcico en la tiza. Aunque nadie resuelve las ecuaciones de la mecánica cuántica para deducir la función de onda detallada o la energía exacta de las moléculas complicadas como las proteínas, no dudamos de que las reglas de la mecánica cuántica explican las propiedades de tales moléculas. Igual sucede con las propiedades de los núcleos atómicos a partir del modelo estándar.
La composición de la tiza (CaCO3) y la proporción de los átomos de los tres elementos que la componen es explicada por la química en términos de los pesos atómicos de cada elemento y del concepto de capa de valencia en la que los electrones son débilmente atraídos por los núcleos. Esta capa es aquella que no se completa como la de los gases nobles.
Aplicando las reglas de la mecánica cuántica se observa que las valencias del calcio, carbono y oxígeno son +2, +4 y -2 respectivamente.
Respecto al peso atómico, casi todo corresponde al núcleo donde conviven protones y neutrones, estos últimos necesarios para reducir la repulsión entre protones y dar estabilidad al núcleo. El peso atómico del protón y del neutrón es muy similar y mucho mayor que el del eléctron, con lo que el peso atómico es proporcional al número total de protones y neutrones del núcleo. Pero:
¿Por qué existe un neutrón y un protón con la carga y masa que tienen?
¿Por qué se atraen mutuamente con una fuerza tan intensa que forman núcleos unas 100.000 veces más pequeños que los propios átomos?
De nuevo la explicación la encontramos en el modelo estándar. Los quarks más ligeros son los llamados u, de up, y d, de down, y tienen cargas +2/3 y -1/3 respectivamente. Los protones son uud y los neutrones udd resultando una carga +1 y neutra respectivamente. Las masas del protón y del neutrón son casi iguales porque se deben esencialmente a las fuerzas fuertes que mantienen ligados a los quarks, y estas son iguales para ambos quarks. El electrón es mucho más ligero porque no siente estas fuerzas fuertes. Todos estos quarks y electrones son gránulos de la energía de diversos campos y sus propiedades se siguen de las propiedades de dichos campos.


Los hadrones son partículas formadas por quarks como los bariones (tres quarks) y los mesones (un quark y un antiquark)
La cadena de por qués nos lleva hasta el modelo estándar, la actual teoría mecanocuántica de las partículas elementales.
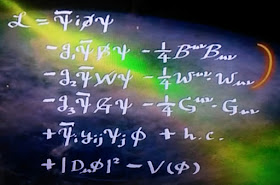
Lagrangiana del modelo estándar a partir de la cual pueden explicarse todos los fenómenos salvo los relacionados con la gravedad
En el caso de la biología por ejemplo, todo lo relacionado con la herencia puede explicarse en términos de la estructura del ADN, una molécula muy grande. Una vez hemos descendido a la química, parece todo más fácil. Aún así, el ADN es demasiado complicado para permitir utilizar las ecuaciones de la mecánica cuántica para establecer su estructura. Pero si se tiene un conocimiento bueno de dicha estructura a partir de las reglas ordinarias de la química, nadie duda que con un ordenador suficientemente potente podríamos explicar todas las propiedades del ADN resolviendo las ecuaciones de la mecánica cuántica.
En ciencias como la biología, la geología o la astronomía el elemento histórico también es necesario además de una ley universal para poder explicar ciertos fenómenos: existe vida que usa el ADN para transmitir la herencia porque existe un planeta Tierra que lo permite. O existe tiza en la Tierra porque los elementos que la forman son, tal y como predice el modelo estándar, de los que se producen más abundantemente en las estrellas y liberados al espacio en las supernovas. Las estrellas a su vez se originan a partír del Hidrógeno y del Helio originado poco después del Big Bang.
Pero este escenario depende de un accidente histórico: la hipótesis de que hubo un Big Bang más o menos homogéneo con aproximadamente 10.000 millones de fotones por cada quark. Sin embargo podría ser que, a diferencia de lo que sucede con la mecánica cuántica y la mecánica newtoniana, las condiciones iniciales aparezcan como parte de las leyes de la naturaleza. Aún así nunca podríamos eliminar los elementos accidentales o históricos en ciencias como la biología, la astronomía o la geología donde con cierta facilidad se dan sistemas con tendencia al caos en los que unas condiciones iniciales casi idénticas pueden llevar a resultados completamente diferentes como en un sistema solar con solo dos planetas.
Imagen de la supernova 1987A tomada por el telescopio Hubble
Pero este escenario depende de un accidente histórico: la hipótesis de que hubo un Big Bang más o menos homogéneo con aproximadamente 10.000 millones de fotones por cada quark. Sin embargo podría ser que, a diferencia de lo que sucede con la mecánica cuántica y la mecánica newtoniana, las condiciones iniciales aparezcan como parte de las leyes de la naturaleza. Aún así nunca podríamos eliminar los elementos accidentales o históricos en ciencias como la biología, la astronomía o la geología donde con cierta facilidad se dan sistemas con tendencia al caos en los que unas condiciones iniciales casi idénticas pueden llevar a resultados completamente diferentes como en un sistema solar con solo dos planetas.
El caos no anula el determinismo de la física newtoniana o precuántica, pero nos obliga a ser muy cuidadosos al decir lo que entendemos por dicho determinismo y a ser precisos en la medida de las condiciones iniciales.
La mecánica cuántica por su parte no es determinista en el mismo sentido en que lo es la mecánica newtoniana. El Principio de Incertidumbre de Heisenberg nos advierte que no podemos medir exactamente la posición y velocidad de una partícula en el mismo instante y que solo podemos predecir probabilidades sobre los resultados de experimentos en cualquier instante posterior. Sin embargo incluso en mecánica cuántica el comportamiento de cualquier sistema físico está completamente determinado por sus condiciones iniciales y las leyes de la naturaleza. Concretamente, la evolución de la función de onda.
La intrusión de accidentes históricos establece límites permanentes a lo que tenemos esperanzas de poder explicar alguna vez. Cualquier explicación de las actuales formas de vida en la Tierra debe considerar la extinción de los dinosaurios hace 65 millones de años, que actualmente se explica por el impacto de un meteorito aunque nadie será capaz de explicar nunca por qué un meteorito chocó con la Tierra precisamente en aquel momento. Lo que más podemos esperar de la ciencia es que seamos capaces de rastrear las explicaciones de todos los fenómenos naturales hasta leyes finales y accidentes históricos.
En el caso del sentido de giro de los planetas alrededor del Sol, este no puede ser deducido de las leyes de Newton porque es una cuestión de historia. Es un grado de libertad de estas leyes. Incluso las leyes de nuestro universo podrían ser un accidente histórico si se demostrara que es uno de los muchos universos de un megaverso. Aún así nuestras leyes serían una solución particular de unas mega leyes finales
Además de la complejidad y los accidentes históricos, la emergencia es otro problema en la cadena de explicaciones hasta las leyes finales. Hay fenómenos emergentes como la inteligencia o la vida que no tienen correspondencia en los niveles más simples como las células vivas individuales o los átomos y las moléculas.
La idea de emergencia también aparece en física y el ejemplo históricamente más importante es la termodinámica, la ciencia del calor originalmente formulada en el siglo XIX por Carnot, Clausius y otros.
La termodinámica era una ciencia autónoma, no deducida de la mecánica de partículas y fuerzas sino basada en conceptos como los de entropía y temperatura que no tienen equivalentes en la mecánica. Solo la Primera Ley de la Termodinámica, la ley de conservación de la energía, proporciona un puente entre la mecánica y la termodinámica. El principio central de la termodinámica era la, Segunda Ley, según la cual los sistemas físicos no poseen solamente una energía y una temperatura sino también una cierta cantidad llamada entropía, que siempre crece con el tiempo en todo sistema cerrado y alcanza un máximo cuando el sistema está en equilibrio.
Los físicos del siglo XIX generalmente tomaban la Segunda Ley de la Termodinámica como un axioma derivado de la experiencia, tan fundamental como cualquier otra ley de la naturaleza pues funcionaba en contextos muy diferentes: comportamiento del vapor o de las reacciones químicas. Incluso actualmente se aplica a los agujeros negros. Si la termodinámica es universal, ¿Cómo puede estar lógicamente relacionada con la física de tipos concretos de partículas y fuerzas?
Más adelante, en la segunda mitad del siglo XIX, Maxwell, Boltzmann y Gibbs demostraron que los principios de la termodinámica podían ser deducidos matemáticamente mediante un análisis de las propiedades de las diferentes configuraciones de ciertos tipos de sistemas, aquellos en que su energía se reparte entre un número muy grande de subsistemas, como es el caso de un gas cuya energía se reparte entre las moléculas que lo componen.
En esta mecánica estadística, la energía térmica de un gas es precisamente la energía cinética de sus partículas; la entropía es una medida del desorden del sistema; y la segunda ley de la termodinámica expresa la tendencia de los sistemas aislados a hacerse más desordenados.
Aunque la termodinámica ha sido explicada en términos de partículas y fuerzas gracias a la mecánica estadística, continúa tratando con conceptos emergentes como los de temperatura o entropía, que pierden todo su significado en el nivel de las partículas elementales. La termodinámica es más un modo de razonar que un cuerpo de leyes físicas universales, pero la mecánica estadística permite que sus explicaciones desciendan hasta el nivel de las partículas elementales y, por tanto, el modelo estándar.
3. Dos Hurras por el reduccionismo
El reduccionismo es un sentido de jerarquía, de que algunas verdades son menos fundamentales que otras a las que las anteriores pueden ser reducidas, como la química puede ser reducida a la física.
Los físicos de partículas elementales, como el autor de este libro, son especialmente susceptibles de ser calificados de reduccionistas pues creen que su área de investigación es la más fundamental de todas.
Especialmente irritados con este reduccionismo de los físicos de partículas están los científicos que investigan en el área de la física de materia condensada (la física de los superconductores, semiconductores y similares) pues consideran que están infrafinanciados y que los físicos de partículas elementales les quitan financiación.
Sin embargo la mecánica cuántica ha tenido un papel fundamental en el descubrimiento del transistor y la teoría fotónica de la luz en la invención del láser y en el desarrollo de todas las comunicaciones ópticas.
La actitud reduccionista proporciona un filtro útil que ahorra a los científicos de todos los campos una pérdida de su tiempo en ideas que no son dignas de ser seguidas.
4. La Mecánica Cuántica y sus descontentos
El descubrimiento de la mecánica cuántica a mediados de los años 20 constituyó la revolución más profunda en la teoría física desde el nacimiento de la física moderna en el siglo XVII. Todas las fantásticas teorías matemáticas que los físicos han desarrollado en los años recientes, las teorías cuánticas de campos, las teorías gauge, las teorías de supercuerdas, están formuladas dentro del marco de la mecánica cuántica. Si existe algo en nuestra comprensión actual de la naturaleza que es probable que sobreviva en una teoría final, ese algo es la mecánica cuántica.
La importancia histórica de la mecánica cuántica no reside solo en el hecho de que proporcione respuestas a un gran número de viejas preguntas acerca de la naturaleza de la materia; mucho más importante es que cambió nuestra idea de las preguntas que podemos plantear.
La mecánica cuántica introdujo una forma completamente nueva de hablar del estado de un sistema. Se utilizan las funciones de onda que solo nos dan información sobre probabilidades.
En 1925 Heisenberg intentó responder a la pregunta de por qué, según el modelo de Bohr, los electrones en los átomos ocupan solo ciertas órbitas permitidas con ciertas energías definidas. Heisenberg adoptó un nuevo punto de partida: solo consideraría magnitudes observables como la energía de los electrones en las órbitas permitidas y los ritmos a los que un electrón puede modificar su estado cuántico espontáneamente emitiendo un fotón.
La importancia histórica de la mecánica cuántica no reside solo en el hecho de que proporcione respuestas a un gran número de viejas preguntas acerca de la naturaleza de la materia; mucho más importante es que cambió nuestra idea de las preguntas que podemos plantear.
La mecánica cuántica introdujo una forma completamente nueva de hablar del estado de un sistema. Se utilizan las funciones de onda que solo nos dan información sobre probabilidades.
En 1925 Heisenberg intentó responder a la pregunta de por qué, según el modelo de Bohr, los electrones en los átomos ocupan solo ciertas órbitas permitidas con ciertas energías definidas. Heisenberg adoptó un nuevo punto de partida: solo consideraría magnitudes observables como la energía de los electrones en las órbitas permitidas y los ritmos a los que un electrón puede modificar su estado cuántico espontáneamente emitiendo un fotón.
A partir de estos ritmos de transición Heisenberg creo una tabla o matriz para cada magnitud: una para la posición, otra para la velocidad, otra para el cuadrado de la velocidad del electrón e introdujo operaciones entre tablas que proporcionaban otras tablas: la multiplicación de matrices. Así pudo calcular una matriz con las energías de los estados cuánticos del átomo. Born, Pascual Jordan y Paul Dirac acabaron de modelar las ideas de Heisenberg dando lugar a la mecánica matricial.
A principios de 1926, Wolfgang Pauli fue capaz de resolver mediante el uso de la nueva mecánica de matrices el problema paradigmático de la física atómica, el cálculo de las energías de los estados cuánticos del átomo de hidrógeno, y justificar así los anteriores resultados de Bohr.
El cálculo mecanocuántico de los niveles energéticos del hidrógeno por Pauli fue una exhibición de brillantez matemática, un uso sagaz de las reglas de Heisenberg y las simetrías especiales del átomo de hidrógeno. Ningún físico fue más perspicaz. Pero ni siquiera Pauli pudo extender este cálculo al Helio y mucho menos a átomos o moléculas más pesados.
Erwin Schrödinger introdujo poco después un formalismo matemático equivalente: la mecánica ondulatoria. Schrödinger demostró también que su mecánica ondulatoria es equivalente a la mecánica matricial de Heisenberg.
La función de onda de una partícula es gobernada por la ecuación de Schrödinger en el caso no relativista
En esta versión, cada estado físico posible de un sistema viene descrito por una función de onda. Esta aproximación ondulatoria ya apareció en 1923 con la dualidad onda-partícula de Louis de Broglie. Para su fórmula supuso que la longitud de onda asociada a un electrón debía ser un número entero de veces la longitud de las órbitas permitidas. Una longitud de onda para el estado de energía más baja, dos para el siguiente y así sucesivamente.
Sin embargo nadie sabía que magnitud física oscilaba en la función de onda. La respuesta vino de un estudio teórico del comportamiento de los electrones libres cuando son disparados contra los átomos. Es natural describir un electrón como un paquete de ondas. La ecuación de Schrödinger muestra que cuando tal paquete de ondas choca contra un átomo, se rompe. Realmente el paquete se rompe antes ya que un paquete de ondas no respresenta un electrón con una velocidad definida sino con una distribución de diferentes velocidades posibles. Las ondas componentes del paquete se dispersan en todas las direcciones. Esto es enigmático porque los electrones que chocan contra un átomo salen en una dirección u otra, pero no se deshacen. Siguen siendo electrones.
En 1926, en Gotinga, Max Born propuso interpretar este comportamiento de la función de onda en términos de probabilidades. El electrón no se rompe, sino que puede ser dispersado en cualquier dirección cuya probabilidad es mayor cuanto más elevado sea el módulo al cuadrado de la función de onda. La función de onda es una onda de probabilidad.
La interpretación probabilística de la mecánica cuántica tuvo el apoyo el año siguiente del Principio de Incertidumbre de Heisenberg. Este dice que no es posible conocer con una precisión absoluta la posición y velocidad de una partícula. Por ejemplo, si queremos medir la posición de un electrón utilizaremos luz de longitud de onda muy corta (fotones de alta energía) que a su vez modificará la velocidad inicial del electrón.
Principio de Incertidumbre formulado por Werner Heisenberg y que constituye el núcleo de la mecánica cuántica
Una onda electrónica que esté muy localizada en una posición representa un electrón que tiene una posición bien definida pero un momento que podría tomar prácticamente cualquier valor y viceversa. En general, los electrones en átomos y moléculas no tienen ni una posición ni un momento bien definidos.
Relacionado con esto, en Mecánica cuántica existe el principio de complementariedad que dice que el conocimiento de un aspecto del sistema impide el conocimiento de otros.
En 1930, en un intento de comprender mejor la mecánica cuántica se llegó a lo que se conoce como interpretación de Copenhague de la mecánica cuántica. Su esencia es una drástica separación entre el aparato de medida y el propio sistema. Durante los intervalos entre mediciones, los valores de la función de onda evolucionan de un modo perfectamente contínuo y determinista según la ecuación de Schrödinger). Mientras esto sigue así no se puede decir que el sistema esté en ninguna configuración definida. Pero en el momento de medir, la función colapsa a un estado definido cuya probabilidad venía dada por su módulo al cuadrado.
La mecánica cuántica no es imprecisa ya que proporciona una herramienta precisa para calcular energías, ritmos de transición y probabilidades. La evolución de la función de onda es tan determinista como las órbitas de las partículas en la mecánica newtoniana. En realidad, es más determinista, porque la ecuación de Schrödinger es demasiado sencilla para permitir soluciones caóticas.
Todo el mundo está de acuerdo en como utilizar la mecánica cuántica pero existen serias discrepancias sobre lo que estamos haciendo cuando la utilizamos. En la física newtoniana no hay estatus especial para los seres humanos mientras que la interpretación de Copenhague les concede un papel esencial al dar significado a la función de onda mediante el acto de medición. Y donde el físico newtoniano hablaba de predicciones exactas, el físico mecanocuántico ofrece solo el cálculo de probabilidades, pareciendo así la existencia del libre albedrío humano o la intervención divina.
La interpretación de Copenhague está basada en una drástica separación entre el sistema físico, gobernado por la mecánica cuántica, y el aparato utilizado para estudiarlo, que se describe clásicamente. Creemos que la mecánica cuántica lo gobierna todo en el universo, no solo los electrones, átomos y moléculas individuales, sino también los aparatos experimentales y a los físicos que los utilizan. Si la función de onda conjunta describe al aparato y al sistema y evoluciona de forma determinista incluso durante la medición, entonces ¿de dónde salen las probabilidades?
Un punto de vista diferente fue el adoptado por Hugh Everett conocido como la interpretación de los muchos mundos o muchas historias de la mecánica cuántica. En esta interpretación la función de onda se desdobla en historias separadas debido a la decoherencia cuántica y evolucionan en universos diferentes sin interferirse entre ellas.
Patrón de interferencia en el experimento de la doble rendija debido a la coherencia cuántica
Podría ser que todas las cuestiones filosóficas profundas sobre el significado de una medición
fueran realmente cuestiones vacías, a las que nos obliga nuestro lenguaje, un lenguaje que evolucionó en un mundo gobernado muy aproximadamente por la física clásica.
También está la cuestión de si la mecánica cuántica es necesariamente verdadera. Debido a la precisión de sus predicciones debe ser una muy buena aproximación. La pregunta es entonces si existe alguna otra teoría lógicamente posible cuyas predicciones sean muy parecidas pero no exactamente las mismas que las de la mecánica cuántica.
La mecánica cuántica es estrictamente lineal. Podemos buscar una teoría alternativa ligeramente no lineal. Sin embargo los efectos no lineales no han sido detectados, con lo que si existen deben de ser muy pequeños. Aunque la teoría correcta no fuera la mecánica cuántica y no fuera lineal, la linealidad de la mecánica cuántica, aunque solo fuera aproximada, es una muy buena aproximación.
Sin embargo lo más difícil no era buscar predicciones y realizar experimentos para confirmar esta teoría alternativa. Lo más desalentador es que esta alternativa no lineal a la mecánica cuántica tenía dificultades internas puramente teóricas. El autor no encontró ninguna forma de extender la versión no lineal de la mecánica cuántica a teorías basadas en la relatividad especial de Einstein. Es difícil modificar la mecánica cuántica sin deshacerla por completo, lo que sugiere que la mecánica cuántica es como es porque modificarla llevaría a absurdos lógicos.
Por ello es posible que la mecánica cuántica sobreviva no simplemente como una aproximación a una teoría más profunda, del modo como la gravitación de Newton sobrevive como una aproximación de la relatividad general, sino como una característica exactamente válida de la teoría final.
5. Historias de teoría y experimento
En las tres historias de este capítulo los físicos se han guiado por su sentido de belleza, no solo al desarrollar nuevas teorías sino incluso también para juzgar teorías ya desarrolladas. Parece que ahora los físicos están aprendiendo a anticipar la belleza de la naturaleza en su nivel más fundamental, lo que podría significar que nos estamos moviendo hacia el descubrimiento de leyes finales de la naturaleza. Estas tres historias son:
- La teoría de la Relatividad General
- La Electrodinámica Cuántica
- La teoría electrodébil
Relatividad General
La relatividad general describe la gravitación como un efecto de la curvatura del espacio-tiempo producida por la materia y la energía.
Uno de los fenómenos de nuestro sistema Solar no explicado correctamente por la teoría de Newton era la precesión del perihelio de Mercurio debido a otros planetas de 575 segundos por siglo. La teoría newtoniana predecía únicamente 532 segundos por siglo.
Valor de la precesión del perihelio de Mercurio donde a es el radio de la órbita, T el periodo y e la excentricidad de la órbita
Esta diferencia de 43 segundos fue solventada por la relatividad general. Uno de los efectos que contribuye a esta precesión extra en la teoría de Einstein es el campo gravitatorio extra producido por la energía del propio campo gravitatorio. En la teoría de Newton la gravitación es producida solo por la masa, pero no por la energía, y no hay tal campo gravitatorio extra.
Después de la guerra, en 1919, se midió la desviación de los rayos luminosos por el Sol de estrellas lejanas durante un eclipse. La relatividad general predice que un rayo de luz que pasa rozando el Sol debe desviarse 1,75 segundos. Para ello los astrónomos midieron la posición de varias estrellas 6 meses antes, cuando el Sol estaba en el lado opuesto y las compararon con las medidas durante el eclipse.

Estos efectos no tenían que suponer a priori que la teoría de Newton debiera ser reemplazada. Anteriormente anomalías como el movimiento de cometas o el de la Luna se habían debido a efectos sutiles no contemplados.
Aunque por algún motivo la predicción de la curvatura de los rayos solares supuso la aceptación de la relatividad, esta no era tan concluyente como la retrodicción del avance del perihelio de Mercurio, que no fue tan considerada como se merecía y que tiene más valor porque explica una desviación conocida y muchas veces medida. Sin embargo en las predicciones, los físicos experimentales pueden buscar correcciones o errores observacionales hasta que los resultados experimentales coinciden con los teóricos (desenfoque del telescopio etc).
A pesar de que al principio la confirmación experimental de la Relatividad General no era contundente, esta era ampliamente aceptada en gran parte debido a su belleza.
En 1905 Einstein desarrolló la Relatividad Especial para solucionar la incompatibilidad existente entre la mecánica clásica y el electromagnetismo haciendo que las ecuaciones de Maxwell fueran válidas independientemente del movimiento del observador.
Sin embargo la Relatividad Especial no encajaba con la teoría de la gravitación de Newton. Por una parte, en la teoría de Newton, la fuerza gravitatoria entre el Sol y un planeta depende de la distancia entre sus posiciones en el mismo instante, pero en la relatividad especial no existe significado absoluto para la simultaneidad: dependiendo de su estado de movimiento, diferentes observadores discreparán sobre si un suceso es anterior, posterior o simultáneo a otro.
Existían varios modos de parchear la teoría de Newton para que fuera compatible con la Relatividad Especial y Einstein ensayó al menos uno (la teoría escalar sin masa). La clave que en 1907 le encaminó hacia la Relatividad General fue una propiedad distintiva de la gravitación: la fuerza de gravedad es proporcional a la masa del cuerpo sobre el que actúa. Así es como las fuerzas inerciales actuan sobre nosotros cuando nos movemos con velocidad o dirección no uniformes. Por ejemplo, en la Tierra no notamos fuerza centrífuga ni campo gravitatorio debido al Sol.
El hecho de que las fuerzas gravitatorias y las inerciales sean ambas proporcionales a la masa del cuerpo sobre el que actúan y no dependan de otras propiedades del cuerpo hacen posible identificar en cualquier punto de cualquier campo gravitatorio un sistema de referencia en caída libre en el que no se sienten las fuerzas gravitatorias ni las inerciales debido a que estan en un equilibrio perfecto para todos los cuerpos. Cuando sentimos las fuerzas gravitatorias o inerciales es porque no estamos en un sistema en caída libre. Einstein dio un salto lógico y conjeturó que las fuerzas gravitatorias y las inerciales eran en el fondo lo mismo. Llamó a esto el principio de equivalencia (de la gravitación y la inercia). Según este principio, cualquier campo gravitatorio queda definido diciendo qué sistema de referencia está en caída libre en cada punto del espacio y el tiempo.
Desde 1907 Einstein pasó una década buscando la estructura matemática que se adaptara a su analogía entre curvatura del espacio-tiempo y gravitación. Finalmente encontró precisamente lo que buscaba en una teoría del espacio curvo que había sido desarrollada por Riemann en el siglo XIX.
En su forma final, la Relatividad General es una reinterpretación en términos de gravitación de la matemática ya existente de los espacios curvos, junto con una ecuación de campo que especificaba la curvatura producida por cualquier cantidad dada de materia y energía. Para las pequeñas masas y velocidades del Sistema Solar, la Relatividad General daba los mismos resultados que la teoría de Newton pero corrigiéndola en minúsculos efectos como la precesión de las órbitas y la desviación de la luz.
Un tercer test de la Relatividad General es el desplazamiento hacia el rojo de las rayas espectrales por la pérdida de energía de los fotones al escapar de la atracción gravitatoria. Esto fue confirmado en 1960 por el experimento de Pound-Rebka.
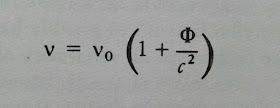
Desplazamiento hacia el rojo de las rayas espectrales
Electrodinámica Cuántica
Es la teoría mecanocuántica de los electrones y la luz. A diferencia de la Relatividad General, esta teoría predecía asombrosamente los experimentos pero en sus inicios tenía problemas de consistencia interna.
La mecánica cuántica fue aplicada a los campos eléctrico y magnético en uno de los primeros artículos sobre mecánica cuántica, el Dreimännerarbeit de Max Born, Werner Heisenberg y Pascual Jordan en 1926. Fueron capaces de calcular que la energía y el momento de los campos electromagnéticos está cuantizada, justificando así la introducción del fotón por Einstein en 1905.
El otro ingrediente principal de la mecánica cuántica fue aportado por Paul Dirac en 1928 con su famosa ecuación que hacía compatible esta teoría con la relatividad especial. Una de las consecuencias más importantes de la teoría de Dirac era la predicción de las antipartículas. En 1932 se descubrió el positrón.
La electrodinámica cuántica permitía calcular correctamente una amplia variedad de procesos físicos:
A mediados de los años 30 sin embargo tenía un problema de consistencia interna cuando se aplicaba a casos de energía elevadas: el problema de los infinitos.
Este problema se manifestó claramente en un artículo de Julius Robert Oppenheimer de 1930 donde intentaba calcular un sutil desplazamiento de la energía de un átomo debido a la emisión y reabsorción de un fotón (virtual) por un electrón sin que ninguno de ellos abandone el átomo. Según el procedimiento de la electrodinámica cuántica, este proceso produce un desplazamiento de la energía del átomo calculable como la suma de infinitas contribuciones, una por cada posible energía del fotón. Esta suma debería ser finita, pero resulta infinita aunque los experimentos muestran que obviamente no lo es.
En 1947 Willis Lamb midió el tipo de efecto que Oppenheimer había intentado calcular en 1930: un desplazamiento de la energía del átomo de hidrógeno debido a la emisión y reabsorción de fotones.
Estrictamente hablando, Lamb midió la diferencia entre los desplazamientos de energía de dos estados del átomo de hidrógeno que, según la antigua teoría de Dirac, en ausencia de emisiones y reabsorciones de fotones tendrían la misma energía, con lo que algo había desplazado las energías de ambos estados en cantidades diferentes.
El desplazamiento de la energía de un átomo debido a la emisión y reabsorción de fotones no es realmente un observable. El único observable es la energía total del átomo, que se calcula añadiendo este desplazamiento de energía a la energía calculada por Dirac en 1928.
Esta energía total depende de la masa desnuda y la carga desnuda del electrón, la masa y la carga que aparecen en la teoría antes de que empecemos a preocuparnos por la emisión y la reabsorción de fotones. Pero los electrones libres, al igual que los electrones en los átomos, siempre están emitiendo y reabsorbiendo fotones que afectan a la masa y la carga del electrón y, por consiguiente, la masa y la carga desnudas no son las mismas que la masa y la carga medidas del electrón. Para explicar los valores observados (finitos) de la masa y la carga del electrón, la masa y la carga desnudas deben ser infinitas.
La energía total del átomo es, por tanto, la suma de dos términos, ambos infinitos: la energía desnuda, que es infinita, y el desplazamiento de la energía de Oppenheimer que también es infinito porque recibe contribuciones de fotones virtuales de energía ilimitada.
Sin embargo Oppenheimer había omitido algo en su cálculo: las contribuciones al desplazamiento de energía de procesos en los que un positrón, un fotón y un segundo electrón surgen espontáneamente del espacio vacío para que, a continuación, el fotón sea absorbido en la aniquilación del positrón y del electrón original. Este extraño proceso debe ser incluido para que la energía del átomo dependa de la velocidad tal y como exige la relatividad especial.
Este es un ejemplo del resultado encontrado previamente por Dirac de que la mecánica cuántica solo es compatible con la relatividad especial si se consideran las antipartículas como el positrón.
Si se considera el proceso positrónico y las diferencias entre las cargas y masas desnudas del electrón y sus valores medidos, entonces parecía que se podían cancelar los infinitos en el desplazamiento de energía.
Hans Bethe fue el primero en intentar calcular nuevamente este desplazamiento de energía, pero siguiendo el procedimiento de Oppenheimer de 17 años antes (sin incluir los positrones y otros efectos relativistas) y descartando las contribuciones de los fotones cuya energía fuera mayor que la asociada a la masa del electrón.
Poco después se refinaron los cálculos incluyendo todos los efectos relativistas y los infinitos se cancelaron sin necesidad de simplificaciones arbitrarias.
La electrodinámica cuántica fue salvada mediante la idea de la cancelación de los infinitos en una redefinición o renormalización de la carga y la masa del electrón.
Pero el problema de los infinitos puede ser resuelto solo si estos aparecen de una manera concreta, lo que ocurre únicamente en un número limitado de teorías cuánticas de campos especialmente simples llamadas renormalizables. La versión más simple de la electrodinámica cuántica es renormalizable y eso explica por qué es como es. Cualquier pequeño cambio haría que fuera inconsistente y que los infinitos no pudieran cancelarse.
Aún así los calculos eran tremendamente complicados y con sumas cuyos términos individuales eran incompatibles com la relatividad especial. Mientras Feynman, Schwinger y Tomonaga estaban desarrollando métodos de cálculo más sencillos y compatibles con la relatividad especial en todos sus pasos.
Utilizaron estos métodos para realizar otros cálculos en asombroso acuerdo con los experimentos, como el del momento magnético del electrón. En 1928 Dirac realizo este cálculo cuyo valor fue corregido en 1,00115965214 (valor medido 1,00115965218±4 en la última cifra decimal) considerando la emisión y reabsorción de fotones virtuales y otros efectos. Es posiblemente el caso más espectacular de acuerdo numérico entre teoría y experimento.
En los físicos el sentido de la belleza es una guía útil para seleccionar ideas y teorías que nos ayudan a explicar la naturaleza.
No es importante para la belleza de una teoría el que sus ecuaciones tengan soluciones elegantes. Las ecuaciones de la Relatividad General resultan difíciles de resolver excepto en las situaciones más sencillas, pero esto no está en contra de la belleza de la teoría misma.
Según el autor, parte de la belleza de una teoría consiste en una simplicidad de ideas, no de la simplicidad de tipo mecánico que puede medirse contando ecuaciones o símbolos.
En la teoría de Newton existen 3 ecuaciones mientras que en la Relatividad General hay 14 (10 de campo y 4 de movimiento). Sin embargo es la teoría de la Relatividad General la que es más bella gracias en parte a la simplicidad de su idea central de equivalencia entre gravitación e inercia.
Otra cualidad de una teoría bella es la inevitabilidad. La teoría de Newton podría no seguir la ley de la inversa del cuadrado sin tener que modificarla sustancialmente. Sin embargo la relatividad debe seguir la ley de la inversa del cuadrado para no aplastar sus bases conceptuales.
El mismo sentido de inevitabilidad puede encontrarse en parte en el modelo estándar de partículas elementales. Ambas teorías tienen una característica común que les aporta parte de esta simplicidad e inevitabilidad: ambas obedecen a principios de simetría.
Un principio de simetría es simplemente una afirmación de que algo se ve igual desde varios puntos de vista, como por ejemplo una esfera o el espacio vacío. Pero lo realmente importante no son las simetrias de las cosas, sino las simetrías de las leyes o principios de invariancia. En general, las leyes de la naturaleza son simétricas o invariantes respecto a la traslación y la rotación espacial o a la traslación temporal. El principio de relatividad de la teoría de la relatividad también es una simetría de la naturaleza. Cualquier principio de simetría es a su vez un principio de simplicidad. Si estas simetrías de las leyes de la naturaleza son importantes en física clásica, su importancia es aún mayor en mecánica cuántica.
Un electrón es idéntico a cualquier otro salvo en su energía, momento y espín. Estas magnitudes son las que caracterizan las formas en que la función de onda responde a transformaciones de simetría. La materia pierde así su papel central en física.
Hoy día se acepta generalmente que la única forma de combinar los principios de la relatividad especial y la mecánica cuántica es a través de una teoría cuántica de campos o algo muy similar. Este es precisamente el tipo de rigidez lógica que da su belleza a una teoría realmente fundamental: la mecánica cuántica y la relatividad especial son casi incompatibles, y su reconciliación en la teoría cuántica de campos impone poderosas restricciones a la forma en que las partículas pueden interaccionar mutuamente.
Una de estas restricciones es que se difumina la diferencia entre campos y partículas. Todo son campos y las partículas son manifestaciones o excitaciones de los campos allí donde su energía es suficiente para crearlas. Y en el caso de las partículas virtuales, ni eso porque gracias al principio de incertidumbre pueden tomar prestada la energía del vacío durante un tiempo suficientemente pequeño. De hecho así funcionan las interacciones, mediante el inintercambio de partículas virtuales.
En el caso del campo electromagnético, la interacción entre dos electrones es debida al intercambio de fotones y la interacción entre un electrón y un fotón por el intercambio de electrones (campo electrónico). La distinción entre materia y fuerza deja de ser esencial porque las partículas de materia también pueden transmitir fuerzas.
Otra de estas restricciones es que la energía y el momento de los campos esta cuantizada. Por ejemplo, en el campo gravitatorio la energía es transportada por los gravitones.
Todas las teorías mencionadas hasta ahora solamente limitan los tipos de fuerzas y materia que una teoría puede contener: en sí mismas no requieren la existencia de ningún tipo particular de materia o fuerza. Los principios de simetría se han vuelto cruciales en las últimas décadas del siglo XX: hay principios de simetría que dictan la existencia misma de todas las fuerzas conocidas de la naturaleza.
El principio de simetría subyacente en la teoría de la relatividad general establece que todos los sistemas de referencia son equivalentes: las mismas leyes son válidas para todos los observadores independientemente de su movimiento. La simetría entre los diferentes sistemas de referencia requiere la existencia de la gravitación. Las diferencias aparentes entre las leyes son en realidad la existencia de un campo gravitatorio.
La simetría subyacente en la teoría electrodébil no es espacio-temporal sino que tiene que ver con la identidad de las partículas. En mecanica cuántica es posible tener una partícula que no es, por ejemplo, ni un electrón ni un neutrino hasta que no se mida una propiedad que las distinga como la carga eléctrica. En la teoría electrodébil, la forma de las leyes de la naturaleza permanece invariable si reemplazamos electrones y neutrinos por estados combinados de ambos.
Esta es la simetría que conecta las fuerzas electromagnéticas con las fuerzas nucleares débiles. El fotón y las partículas W± y Z aparecen en la teoría electrodébil como paquetes de energía de cuatro campos, campos que son requeridos por esta simetría de la teoría electrodébil de igual forma que el campo gravitatorio es requerido por las simetrías de la relatividad general.
Estas simetrías se denominan simetrías internas porque estan relacionadas con la naturaleza intrínseca de las partículas más que con su posición o movimiento. La invariancia de las leyes de la naturaleza bajo un grupo de tales transformaciones de simetría interna dependientes de la posición y el tiempo se denomina simetría local o gauge.
Es la simetría local entre diferentes sistemas de referencia en el espacio y en el tiempo lo que hace necesaria la gravitación y, análogamente, es una segunda simetría local entre electrones y neutrinos lo que hace necesaria la existencia del campo fotónico, del campo W y del campo Z.
Todavía existe una tercera simetría local exacta asociada con la propiedad interna de los quarks conocida como carga de color. Cada uno de los 6 tipos o sabores de quarks se da en tres colores: rojo, blanco y azul. Pues existe una simetría exacta de la naturaleza entre los diferentes colores. La fuerza entre un quark rojo y uno blanco es la misma que entre un quark blanco y uno azul, y la fuerza entre dos quarks rojos es la misma que entre dos quarks azules.
Pero esta simetría va más allá del mero intercambio de colores. En mecánica cuántica podemos considerar estados de un solo quark que no son ni exactamente rojos ni exactamente blancos ni exactamente azules. Las leyes de la naturaleza toman exactamente la mismisma forma si reemplazamos los quarks rojos, blanco y azul por quarks en tres combinaciones de estados apropiada.
En analogía con la relatividad general, el hecho de que las leyes de la naturaleza no se vean afectadas al variar de un lugar a otro y de un instante a otro hace necesario incluir en la teoría una familia de campos que interaccionan con los quarks, análogos al campo gravitatorio. Son ocho campos que se conocen como campos gluónicos. La teoría de tales fuerzas, la cromodinámica cuántica, es sencillamente la teoría de quarks y gluones que respeta esta simetría de color local. El modelo estándar de las partículas elementales consiste en la teoría electrodébil ccombinada com la cromodinámica cuántica.
No solo los principios de simetría dan una especie de rigidez o inevitabilidad a las teorías. Únicamente con estos principios la teoría electrodébil o la cromodinámica cuántica serían solo uno de los muchos tipos de teorías posibles. La restricción adicional que nos permite escoger nuestro modelo estándar sencillo de entre la variedad de teorías más complicadas que satisfacen los mismos principios de simetría es que sea renormalizable. Resulta que esta condición impone un alto grado de simplicidad a las ecuaciones de la teoría y, junto con las diversas simetrías locales, sigue un largo camino hasta dar una forma única a nuestro modelo estándar de las partículas elementales.
La rigidez, simplicidad e inevitabilidad que conducen a la belleza parecen no darse en el modelo estándar por la gran cantidad de parámetros ajustables arbitrariamente y en la aparente aleatoriedad de sus valores. Sin embargo lo importante es disponer de un conjunto sencillo de principios que explique por qué las partículas son las que son independientemente de su cantidad o de sus propiedades.
De forma extraña e inquietante, aunque la belleza de las teorías físicas está incorporada en estructuras matemáticas rígidas basadas en principios subyacentes simples, las estructuras que tienen este tipo de belleza tienden a sobrevivir incluso cuándo se descubre que los principios subyacentes están equivocados.
Un buen ejemplo es la teoría de Dirac del electrón con la que en 1928 obtuvo una versión relativista de la ecuación de Schrödinger en términos de ondas de partículas. Esta teoría predijo el espín del electrón y la antimateria.
Esta teoría era un ingrediente clave de la electrodinámica cuántica en los años 30 y 40. Pero hoy sabemos que el punto de vista de Dirac era equivocado pues el contexto adecuado para la reconciliación de la mecánica cuántica con la relatividad especial es el formalismo conocido como teoría cuántica de campos, presentada por Heisenberg y Pauli en 1929 donde todas las partículas son cuantos de su campo asociado.
Casi por accidente la teoría de Dirac daba los mismos resultados que la teoría cuántica de campos para procesos que sólo involucran fotones, electrones y positrones. Pero la teoría cuántica de campos es más general: puede explicar por ejemplo la desintegración beta. En la teoría de Dirac los electrones son eternos y la creación de un par electrón-positrón se explica como el ascenso de un electrón de energía negativa a un estado de energía positiva dejando un hueco en el mar de electrones de energía negativa que es observado como un positrón. La aniquilación de un electrón y un positrón se interpreta como la caida de un electrón en un hueco. Sin embargo, en la desintegración beta se crean electrones sin positrones a partir de la energía y de la carga de vacío.
Por otro lado no hay nada en las teorías cuánticas de campos que requiera que las partículas tengan un espín concreto. El electrón resulta tener el espín que la teoría de Dirac requería, pero existen otras partículas con otros espines que, a su vez, tienen antipartículas y esto no tiene nada que ver con las energías negativas sobre las que especuló Dirac. Pese a todo, las matemáticas de la teoría de Dirac han sobrevivido como una parte esencial de la teoría cuántica de campos. Así la estructura formal de la teoría de Dirac ha sobrevivido a la muerte de los principios de la mecánica cuántica relativista que siguió Dirac para llegar a su teoría. Algo similar sucedió con el modelo de Bohr. Sus principios subyacentes han sido abandonados, pero aún utilizamos algo de su lenguaje y métodos de cálculo. Es curioso como algunas estructuras matemáticas bellas pueden ser trasladadas de un marco conceptual a otro. Como si la belleza fuera algo intrínseco o esencial del mundo esperando los principios adecuados que debe describir.
Otro ejemplo es la bella geometría riemanniana desarrollada exclusivamente por motivaciones matemáticas desconociendo sus aplicaciones físicas. Su belleza era de nuevo la de la inevitabilidad. Posteriormente la Relatividad General la ha tomado como la estructura matemática que la describe perfectamente.
Un ejemplo aún más extraño lo proporciona la historia de los principios de simetría interna. En física estos principios imponen típicamente una estructura de familias en la lista de partículas posibles. Estas transformaciones contínuas de simetría actúan sobre la etiqueta de las partículas de un modo que es matemáticamente equivalente a la forma en que las rotaciones ordinarias en tres dimensiones actúan sobre los espines de las partículas como protones, neutrones o electrones transformándolas en partículas que son combinaciones de varias de ellas con probabilidades arbitrarias de ser un protón, un neutrón o un electrón.
Por ello hasta los años 60 muchos físicos creyeron que las transformaciones de simetría interna que dejan invariantes las leyes de la naturaleza debían ser rotaciones en un cierto espacio de dos, tres o más dimensiones. Al descubrirse nuevas partículas a finales de los años cincuenta se tuvieron que introducir otros tipos de simetría interna. En 1960 los físicos teóricos se llevaron la grata sorpresa de que los matemáticos ya habían catalogado todas las simetrías posibles. El conjunto completo de transformaciones que deja inalterada cualquier cosa, ya sea un objeto específico o las leyes de la naturaleza, constituye una estructura matemática conocida como grupo y la matemática general de las transformaciones de simetría es conocida como teoría de grupos. La lista de los tipos de familias permitidas por cualquier simetría particular de las leyes de la naturaleza esta completamente determinada por la estructura matemática del grupo de simetría.
Las transformaciones que actuan de forma continua, como las rotaciones en el espacio ordinario o la combinación de electrones y neutrinos en la teoría electrodébil, se denominan grupos de Lie. Existen unos grupos de Lie simples a partir de los cuales pueden construirse todos los demás combinando sus transformaciones. En 1960 Gell-Mann descubrió que uno de estos grupos de Lie simples SU(3) era exactamente el necesario para imponer a la multitud de partículas elementales una estructura de familias similar a la que se había descubierto experimentalmente. Uno de los grandes éxitos de la nueva simetría SU(3) fue predecir una nueva partícula para completar una de las familias que fue descubierta con la masa predicha.
Aunque todavía no tenemos una idea segura de si en física fundamental podemos confiar en nuestro sentido de la belleza, en fisica de partículas elementales los juicios estéticos parecen estar trabajando cada vez mejor. Esto podría ser una evidencia de que vamos en la buena dirección y de que quizás no estamos demasiado lejos de nuestro objetivo.
En este capítulo el autor se pregunta si la filosofía puede proporcionar a los físicos una guía hacia la teoría final de igual modo que los juicios estéticos. La opinión del autor es un rotundo no. Ni siquiera la filosofía de la ciencia a la que considera, como mucho, una recopilación agradable sobre la historia y los descubrimientos de la ciencia.
Aunque el autor valora obras de autores como Wittgenstein o Paul Feyerabend, considera que tienen poco que ver con el trabajo de la ciencia.
Wigner hablaba de la «irrazonable efectividad» de la matemática. Para el autor también se da la irrazonable inefectividad de la filosofía.
La doctrina del mecanicismo proporcionó mas molestia que utilidad debido al tiempo en que se perpetuó. Fue un antídoto al culto de los dioses y demonios en la antigua grecia. Fue ampliamente utilizada por Descartes, lo que a su vez influyó en Newton. El mecanicismo estaba tan arraigado que la idea de la gravitación de Newton con la acción a distancia tardó mucho en arraigar y fue gracias a filósofos como Kant y Voltaire. El único aspecto positivo de la filosofía es liberar a la ciencia de prejuicios filosóficos.
Incluso la teoría del campo electromagnético de Faraday y Maxwell fue originalmente formulado de manera mecanicista mediante el éter. La tradición mecanicista no fue definitivamente superada hasta el año 1905 con la relatividad especial.
Aún así en física de partículas se conservaba la distinción, de reminiscencia mecanicista, entre partículas de materia y mediadoras de fuerzas. Finalmente la teoría cuántica de campos formulada por Heisenberg y Pauli en 1929 eliminó esta separación: solo hay campos.
No sabemos si la clave de las teorías futuras estará en la partícula última de materia o en la unificación final de todas las fuerzas. Tampoco sabemos si esas son las preguntas correctas. Parece poco probable la resurrección del mecanicismo o el tener que volver a un dualismo de partículas y campos. Pero ni siquiera la teoría cuántica de campos es segura pues existen dificultades para incluir en ellas la gravitación. Probablemente no sepamos las preguntas correctas hasta estar cerca de las respuestas.
Aparte del mecanicismo, hay otras presuposiciones metafísicas que continúan molestando a la física, especialmente aquellas que tienen que ver con el espacio y el tiempo.
Kant enseñaba que el espacio y el tiempo no son parte de la realidad externa sino que más bien son estructuras preexistentes en nuestras mentes y que podíamos aprender sobre ellos mediante la razón pura. Para un kantiano era muy sorprendente que el espacio y el tiempo se pudiera ver afectado por el movimiento y la gravitación, fenómenos ajenos a la razón y por tanto no comprensibles por esta únicamente.
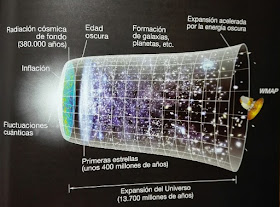
El tiempo no es eterno y puede no haber existido eternamente. Si el tiempo se creó en el Big Bang no tiene sentido preguntarse qué había antes. San Agustín en sus confesiones llegó a la conclusión de que Dios, que está fuera del tiempo, creó el tiempo junto al universo.
Hay teorías basadas en el universo inflacionario de un multiverso infinitamente viejo en el que nuestro universo en expansión es solo uno de las infinitos universos burbuja que contiene. Sobre la base del entendimiento puro no es posible concluir si el tiempo tiene una edad finita o no.
La doctrina epistemológica del positivismo también puede ser un freno al avance científico. Esta doctrina demanda no solo que la ciencia deba contrastar sus teorías frente a la observación, sino que todo aspecto de nuestras teorías debe en todo punto referirse a magnitudes observables.
Ernst Mach es considerado como la persona que introdujo el positivismo en la física y para quién esta doctrina sirvió de antídoto a la metafísica de Kant. Físico y filosofo de Viena, influenció a Einstein cuya relatividad especial está llena de observadores y relojes. También influenció a Heisenberg en el Principio de Incertidumbre y alejando de la mecánica cuántica (basada hasta entonces en el modelo de Bohr) magnitudes inobservables como la posición y la velocidad, sustituidas por la energía y los ritmos de transición.
Pero el positivismo ha hecho tanto daño como bien, por ejemplo, dificultando la aceptación de la teoría atómica de Dalton y Avogadro y de la exitosa mecánica estadística de Maxwell, Boltzmann y Gibbs al considerar que los átomos no pueden ser observados.
El positivismo también jugó un papel oscurecedor en el problema de los infinitos de la electrodinámica cuántica retrasando su solución mediante una cuidadosa definición de la masa y la carga del electrón.
También en las teorías cuánticas de campos el positivismo fue negativo al intentar calcular la matriz S de scattering (dispersión) solo mediante magnitudes observables excluyendo los campos cuánticos, lo cuál era mucho más complicado. La matriz S es la tabla de probabilidades de todos los resultados posibles de todas las colisiones posibles entre partículas. Esta matriz resume todo lo que es realmente observable en las reacciones que involucran cualquier número de partículas. Su origen se remonta al trabajo de Heisenberg y Wheeler en los años 30 y 40.
El abandono más espectacular de los principios del positivismo se ha producido en el desarrollo de la teoría actual de los quarks, la cromodinámica cuántica. En esta teoría se da la propiedad de la libertad asintótica, que impide cualquier proceso en el que un quark pueda quedar aislado. Esta propiedad se da en algunas teorías cuánticas de campos (teorías gauge no abelianas o de Yang-Mills) como mostraron en 1973 David Gross, Frank Wilczek y David Politzer y consiste en que las fuerzas en dichas teorías decrecen a altas energías. La libertad asintótica y el hecho de que los gluones tengan masa nula hace que estos y los quarks no puedan ser observados. La razón está en que el intercambio de gluones sin masa entre quarks y gluones producen fuerzas de largo alcance que impiden tirar de ellos para dejarlos sueltos. La cromodinámica cuántica gobierna pues partículas no observables, justo al contrario de lo que requiere el positivismo.
Si el modelo estándar tiene gran poder predictivo, ¿por qué los físicos teóricos están tan tristes?
Los motivos son varios:
Muchas características del modelo estándar no están dictadas por principios fundamentales, sino que deben ser tomadas de la experiencia. Estas características aparentemente arbitrarias incluyen:
Por todo ello el modelo estándar claramente no es la respuesta final. Todos estos problemas del modelo estándar tienen que ver con la ruptura espontánea de simetría. El descubrimiento de este fenómeno ha sido uno de los grandes desarrollos liberadores de la ciencia del siglo XX. Su mayor éxito fue la explicación de las diferencias entre la fuerza electromagnética y la fuerza nuclear débil.
La teoría electrodébil está basada en un principio de simetría exacta, que dice que las leyes de la naturaleza son invariantes si en sus ecuaciones reemplazamos los campos del electrón y del neutrino por campos combinados de ambos, y al mismo tiempo combinamos análogamente los campos de las otras familias de partículas como el quark up y el quark down. Este principio de simetría es local porque estas combinaciones pueden variar con la posición y el tiempo.
Esta simetría es una propiedad de las ecuaciones subyacentes en el modelo estándar, pero esta simetría no es satisfecha por las soluciones de dichas ecuaciones, es decir, por las propiedades de las propias partículas. Por eso los bosones W± y Z tienen masa pero el fotón no. Igual pasa con el electrón y el neutrino. Las masas concretas de estas partículas son una situación particular de las ecuaciones. La simetría de las ecuaciones no está necesariamente reflejada en cada solución individual de dichas ecuaciones, sino solo en el conjunto total de todas las soluciones de las ecuaciones. La naturaleza tal como la conocemos es sólo una solución de todas las ecuaciones del modelo estándar, y no supone ninguna diferencia qué solución sea con tal de que todas las diferentes soluciones estén relacionadas mediante principios de simetría exacta.
En tales casos decimos que la simetría está rota. Llamamos a este fenómeno una ruptura espontánea de simetría porque nada rompe la simetría en las ecuaciones de la teoría. La ruptura de simetría aparece espontáneamente en las diversas soluciones de estas ecuaciones. Hay mas simetría y belleza en las leyes de la naturaleza de lo que parece por simple observación. Un ejemplo de simetría rota es un imán, que por debajo de 770° desarrolla un campo magnético en cierta dirección aunque las ecuaciones que lo gobiernan son espacialmente simétricas.
En el caso de la teoría electrodébil existe una ruptura espontánea de simetría que se manifiesta en una diferencia de masa entre el fotón y los bosones W± y Z que a su vez hace que la intensidad y el alcance de ambas difiera.
La ruptura espontánea de simetría de la fuerza electrodébil se debe a la presencia de un campo cuyo valor de vacío es no nulo. Es este valor diferente de cero lo que hace que la simetría se rompa. Como todos los campos cuánticos, la energía y el momento de este nuevo campo viene en paquetes, el bosón de Higgs.
Con la inclusión del campo de Higgs todas las partículas tienen masa nula salvo el bosón de Higgs, cuya masa es la única que aparece en el modelo estándar. Todas las demás partículas adquieren una masa proporcional al bosón de Higgs mediante el mecanismo de ruptura espontánea de la simetría electrodébil. Por tanto conocer el origen de la masa sería equivalente a entender el mecanismo de ruptura espontánea de simetría. Es posible que en el origen del universo la simetría electrodébil no estuviera rota, y que se rompiera pocos instantes después al bajar la temperatura de un umbral.
El concepto de ruptura espontánea de simetría también se ha utilizado para intentar incluir la fuerza nuclear fuerte dentro del mismo marco unificado que las fuerzas débil y electromagnética. Sin embargo no existe una simetría en las ecuaciones del modelo estándar que relacionen las fuerzas nucleares fuertes con la débil y la electromagnética. Desde los 70 se buscó una teoría subyacente al modelo estándar en que las tres interacciones quedaran unificadas mediante un único y gran grupo de simetrías espontáneamente rotas como SU(5).
Un obstáculo obvio de estas teorías es la diferencia entre las intensidades intrínsecas entre las tres fuerzas. Estas intensidades determinan las fuerzas junto a la masa de la partícula mediadora y caracterizan la probabilidad de que partículas como los fotones, gluones, W± o Z sean emitidas y reabsorbidas en las reacciones entre partículas. La simetría exigiría que estas tres intensidades fueran iguales cosa que no sucede en la realidad ni aunque fuera debido a una simetría rota.
Una posible solución sería que las intensidades de las tres fuerzas se igualaran a una energía extremadamente alta mucho mayor que la alcanzable con los experimentos actuales, una centésima parte de la energía de Planck. La energía debe ser elevada porque la intensidad intrínseca de la fuerza nuclear fuerte desciende muy lentamente con la energía. Además, a la energía de Planck la fuerza gravitatoria se haría tan intensa como el resto de fuerzas unificándose con ellas.
El hecho de que la energía de unificación electrodébil y fuerte y la energía de Planck estén próximas sugiere que la ruptura de cualquier simetría que una las fuerzas fuerte y electrodébil es solo parte de una ruptura de simetría más fundamental: la ruptura de cualquier simetría que relacione la gravitación con las demás fuerzas de la naturaleza. Podría existir una teoría unificada que englobe las cuatro fuerzas de la naturaleza conocidas.
Por desgracia, la razón de que la gravitación quede fuera del modelo estándar es que resulta muy difícil describir la gravitación en el lenguaje de la teoría cuántica de campos. Podemos aplicar simplemente las reglas de la mecánica cuántica a las ecuaciones de campo de la relatividad general, pero entonces entramos en el viejo problema de los infinitos. Por ejemplo se obtienen probabilidades infinitas en lo que sucede en colisiones de dos gravitones que intercambian más de un gravitón.
El valor tan elevado de la energía de Planck nos enfrenta a otro gran problema. Esta energía surge en un nivel tan profundo que podemos suponer que es la unidad fundamental de energía que aparece en las ecuaciones de la teoría final. El misterio está en por qué todas las demás energías son tan pequeñas. La masa del bosón de Higgs se estima 100 billones de veces más pequeña que la energía de Planck. Esto significa que hay una jerarquía de simetrías: cualquiera que sea la simetría que unifica las fuerzas gravitatoria y nuclear fuerte con las fuerzas electrodébiles se rompe aproximadamente 100 billones de veces más fuertemente que la simetría que unifica las interacciones débiles y electromagnéticas. Esto se conoce como el problema de la jerarquía.
Una aproximación a este problema se basa en la supersimetría, una nueva simetría que relaciona partículas de diferente espín de modo que forman nuevas «superfamilias». En estas teorías la masa del bosón de Higgs sería nula en las ecuaciones fundamentales de la teoría y aparecería a partir de un complicado mecanismo de ruptura de la supersimetría.
Más allá del problema de la jerarquía, la conjetura de que todas las fuerzas de la naturaleza se unificarán a una energía del orden de la energía de Planck ha arrojado una nueva luz sobre el problema de los infinitos. La condición de renormalización fue una poderosa guía para la construcción del modelo estándar. Pero como el modelo estándar deja fuera la gravitación, se cree que es simplemente una aproximación válida a baja energía a una teoría unificada realmente fundamental y que pierde su validez a energías como la energía de Planck. Por eso el problema de los infinitos no ha desaparecido, sino que es un problema para la teoría final, no para una aproximación a baja energía como parece ser el modelo estándar.
Podría ser que las ecuaciones del modelo estándar no son del tipo muy simple que sería renormalizable, sino que contienen cualquier término concebible consistente con las simetrías de la teoría. Estos nuevos términos no renormalizables aparecerían divididos por potencias de alguna cantidad del orden de la energía de Planck, que a bajas energías serían despreciables. La condición de renormalización era correcta a efectos prácticos aunque no lógicamente necesaria.
Estos nuevos términos hacen que algunas magnitudes no se conserven, como la del número de quarks o el número leptónico. La primera impide la desintegración del protón en un positrón y un fotón y garantizaría la estabilidad de la materia. La segunda hacía que el neutrino tuviera masa nula. Experimentos como el super Kamiokande de Japón han mostrado que los neutrinos tendrían una masa minúscula con lo que no se conservaría el número leptónico. Esto hace que el neutrino pueda mutar de un tipo a otro (electrónico, muónico y tau) y explicaría por qué históricamente siempre se había detectado menos neutrinos del primer tipo de los esperados procedentes del Sol.
Después de la guerra, en 1919, se midió la desviación de los rayos luminosos por el Sol de estrellas lejanas durante un eclipse. La relatividad general predice que un rayo de luz que pasa rozando el Sol debe desviarse 1,75 segundos. Para ello los astrónomos midieron la posición de varias estrellas 6 meses antes, cuando el Sol estaba en el lado opuesto y las compararon con las medidas durante el eclipse.
Desviación de los rayos luminosos por el Sol

El ángulo de desviación de los rayos luminosos por el Sol es de 1,7 segundos por cada diámetro solar de distancia al Sol
Aunque por algún motivo la predicción de la curvatura de los rayos solares supuso la aceptación de la relatividad, esta no era tan concluyente como la retrodicción del avance del perihelio de Mercurio, que no fue tan considerada como se merecía y que tiene más valor porque explica una desviación conocida y muchas veces medida. Sin embargo en las predicciones, los físicos experimentales pueden buscar correcciones o errores observacionales hasta que los resultados experimentales coinciden con los teóricos (desenfoque del telescopio etc).
A pesar de que al principio la confirmación experimental de la Relatividad General no era contundente, esta era ampliamente aceptada en gran parte debido a su belleza.
En 1905 Einstein desarrolló la Relatividad Especial para solucionar la incompatibilidad existente entre la mecánica clásica y el electromagnetismo haciendo que las ecuaciones de Maxwell fueran válidas independientemente del movimiento del observador.
La equivalencia entre masa y energía es uno de las principales consecuencias de la Relatividad Especial
Sin embargo la Relatividad Especial no encajaba con la teoría de la gravitación de Newton. Por una parte, en la teoría de Newton, la fuerza gravitatoria entre el Sol y un planeta depende de la distancia entre sus posiciones en el mismo instante, pero en la relatividad especial no existe significado absoluto para la simultaneidad: dependiendo de su estado de movimiento, diferentes observadores discreparán sobre si un suceso es anterior, posterior o simultáneo a otro.
Ecuaciones de Maxwell
Existían varios modos de parchear la teoría de Newton para que fuera compatible con la Relatividad Especial y Einstein ensayó al menos uno (la teoría escalar sin masa). La clave que en 1907 le encaminó hacia la Relatividad General fue una propiedad distintiva de la gravitación: la fuerza de gravedad es proporcional a la masa del cuerpo sobre el que actúa. Así es como las fuerzas inerciales actuan sobre nosotros cuando nos movemos con velocidad o dirección no uniformes. Por ejemplo, en la Tierra no notamos fuerza centrífuga ni campo gravitatorio debido al Sol.
El hecho de que las fuerzas gravitatorias y las inerciales sean ambas proporcionales a la masa del cuerpo sobre el que actúan y no dependan de otras propiedades del cuerpo hacen posible identificar en cualquier punto de cualquier campo gravitatorio un sistema de referencia en caída libre en el que no se sienten las fuerzas gravitatorias ni las inerciales debido a que estan en un equilibrio perfecto para todos los cuerpos. Cuando sentimos las fuerzas gravitatorias o inerciales es porque no estamos en un sistema en caída libre. Einstein dio un salto lógico y conjeturó que las fuerzas gravitatorias y las inerciales eran en el fondo lo mismo. Llamó a esto el principio de equivalencia (de la gravitación y la inercia). Según este principio, cualquier campo gravitatorio queda definido diciendo qué sistema de referencia está en caída libre en cada punto del espacio y el tiempo.
Desde 1907 Einstein pasó una década buscando la estructura matemática que se adaptara a su analogía entre curvatura del espacio-tiempo y gravitación. Finalmente encontró precisamente lo que buscaba en una teoría del espacio curvo que había sido desarrollada por Riemann en el siglo XIX.
Ecuaciones de la teoría general de la relatividad
Un tercer test de la Relatividad General es el desplazamiento hacia el rojo de las rayas espectrales por la pérdida de energía de los fotones al escapar de la atracción gravitatoria. Esto fue confirmado en 1960 por el experimento de Pound-Rebka.
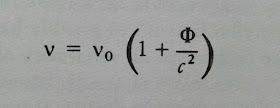
Desplazamiento hacia el rojo de las rayas espectrales
Electrodinámica Cuántica
Es la teoría mecanocuántica de los electrones y la luz. A diferencia de la Relatividad General, esta teoría predecía asombrosamente los experimentos pero en sus inicios tenía problemas de consistencia interna.
La mecánica cuántica fue aplicada a los campos eléctrico y magnético en uno de los primeros artículos sobre mecánica cuántica, el Dreimännerarbeit de Max Born, Werner Heisenberg y Pascual Jordan en 1926. Fueron capaces de calcular que la energía y el momento de los campos electromagnéticos está cuantizada, justificando así la introducción del fotón por Einstein en 1905.
El otro ingrediente principal de la mecánica cuántica fue aportado por Paul Dirac en 1928 con su famosa ecuación que hacía compatible esta teoría con la relatividad especial. Una de las consecuencias más importantes de la teoría de Dirac era la predicción de las antipartículas. En 1932 se descubrió el positrón.
Ecuación de Dirac
La electrodinámica cuántica permitía calcular correctamente una amplia variedad de procesos físicos:
- La dispersión de un fotón que colisiona con un electrón.
- La dispersión de un electrón por otro.
- La aniquilación o producción de un electrón y positrón.
A mediados de los años 30 sin embargo tenía un problema de consistencia interna cuando se aplicaba a casos de energía elevadas: el problema de los infinitos.
Este problema se manifestó claramente en un artículo de Julius Robert Oppenheimer de 1930 donde intentaba calcular un sutil desplazamiento de la energía de un átomo debido a la emisión y reabsorción de un fotón (virtual) por un electrón sin que ninguno de ellos abandone el átomo. Según el procedimiento de la electrodinámica cuántica, este proceso produce un desplazamiento de la energía del átomo calculable como la suma de infinitas contribuciones, una por cada posible energía del fotón. Esta suma debería ser finita, pero resulta infinita aunque los experimentos muestran que obviamente no lo es.
En 1947 Willis Lamb midió el tipo de efecto que Oppenheimer había intentado calcular en 1930: un desplazamiento de la energía del átomo de hidrógeno debido a la emisión y reabsorción de fotones.
Estrictamente hablando, Lamb midió la diferencia entre los desplazamientos de energía de dos estados del átomo de hidrógeno que, según la antigua teoría de Dirac, en ausencia de emisiones y reabsorciones de fotones tendrían la misma energía, con lo que algo había desplazado las energías de ambos estados en cantidades diferentes.
El desplazamiento de la energía de un átomo debido a la emisión y reabsorción de fotones no es realmente un observable. El único observable es la energía total del átomo, que se calcula añadiendo este desplazamiento de energía a la energía calculada por Dirac en 1928.
Esta energía total depende de la masa desnuda y la carga desnuda del electrón, la masa y la carga que aparecen en la teoría antes de que empecemos a preocuparnos por la emisión y la reabsorción de fotones. Pero los electrones libres, al igual que los electrones en los átomos, siempre están emitiendo y reabsorbiendo fotones que afectan a la masa y la carga del electrón y, por consiguiente, la masa y la carga desnudas no son las mismas que la masa y la carga medidas del electrón. Para explicar los valores observados (finitos) de la masa y la carga del electrón, la masa y la carga desnudas deben ser infinitas.
La energía total del átomo es, por tanto, la suma de dos términos, ambos infinitos: la energía desnuda, que es infinita, y el desplazamiento de la energía de Oppenheimer que también es infinito porque recibe contribuciones de fotones virtuales de energía ilimitada.
Sin embargo Oppenheimer había omitido algo en su cálculo: las contribuciones al desplazamiento de energía de procesos en los que un positrón, un fotón y un segundo electrón surgen espontáneamente del espacio vacío para que, a continuación, el fotón sea absorbido en la aniquilación del positrón y del electrón original. Este extraño proceso debe ser incluido para que la energía del átomo dependa de la velocidad tal y como exige la relatividad especial.
Diagrama de Feynman en que un electrón se aniquila con un positrón. El fotón resultante se transforma posteriormente en un nuevo par electrón-positrón
Este es un ejemplo del resultado encontrado previamente por Dirac de que la mecánica cuántica solo es compatible con la relatividad especial si se consideran las antipartículas como el positrón.
Si se considera el proceso positrónico y las diferencias entre las cargas y masas desnudas del electrón y sus valores medidos, entonces parecía que se podían cancelar los infinitos en el desplazamiento de energía.
Hans Bethe fue el primero en intentar calcular nuevamente este desplazamiento de energía, pero siguiendo el procedimiento de Oppenheimer de 17 años antes (sin incluir los positrones y otros efectos relativistas) y descartando las contribuciones de los fotones cuya energía fuera mayor que la asociada a la masa del electrón.
Poco después se refinaron los cálculos incluyendo todos los efectos relativistas y los infinitos se cancelaron sin necesidad de simplificaciones arbitrarias.
La electrodinámica cuántica fue salvada mediante la idea de la cancelación de los infinitos en una redefinición o renormalización de la carga y la masa del electrón.
Pero el problema de los infinitos puede ser resuelto solo si estos aparecen de una manera concreta, lo que ocurre únicamente en un número limitado de teorías cuánticas de campos especialmente simples llamadas renormalizables. La versión más simple de la electrodinámica cuántica es renormalizable y eso explica por qué es como es. Cualquier pequeño cambio haría que fuera inconsistente y que los infinitos no pudieran cancelarse.
Aún así los calculos eran tremendamente complicados y con sumas cuyos términos individuales eran incompatibles com la relatividad especial. Mientras Feynman, Schwinger y Tomonaga estaban desarrollando métodos de cálculo más sencillos y compatibles con la relatividad especial en todos sus pasos.
Lagrangiana de la Electrodinámica Cuántica, la teoría que describe como interacciona la luz con la materia. M es la masa del electrón, A es el potencial vector del electromagnetismo y F es el tensor electromagnético. Los dos primeros corresponden a la ecuación de Dirac, el tercero es el de interacción entre el electrón y el fotón (consecuencia de la simetría gauge) y el cuarto es el de la propagación del fotón en ausencia de fuentes (onda electromagnética)
Utilizaron estos métodos para realizar otros cálculos en asombroso acuerdo con los experimentos, como el del momento magnético del electrón. En 1928 Dirac realizo este cálculo cuyo valor fue corregido en 1,00115965214 (valor medido 1,00115965218±4 en la última cifra decimal) considerando la emisión y reabsorción de fotones virtuales y otros efectos. Es posiblemente el caso más espectacular de acuerdo numérico entre teoría y experimento.
Fuerza Nuclear Débil
Esta fuerza juega un papel esencial en las cadenas de reacciones nucleares que generan energía y producen los diferentes elementos químicos en los núcleos de las estrellas.
Esta fuerza quedó de manifiesto por primera vez en el descubrimiento de la radiactividad por Henri Becquerel en 1896. La radiación beta origen de esta radiactividad consiste en que un neutrón se convierta en un protón a la vez que se crea un electrón y un antineutrino que son expulsados del núcleo. Este cambio de identidad de las partículas es algo que no está permitido por ninguna otra fuerza de las conocidas anteriormente.
La fuerza nuclear débil es mucho menos intensa que las fuerzas electromagnética o nuclear fuerte. Esto queda de manifiesto en que es una fuerza lenta ya que cualquier proceso en el que interviene dura una centésima de segundo, cuando la nuclear fuerte necesita solo 10-24s. Otra característica peculiar es que presenta una asimetría izquierda-derecha o quiralidad.
En 1933 Enrico Fermi desarrolló una teoría de la fuerza nuclear débil en la que la fuerza no actúa a distancia, sino que el neutrón, el electrón y el antineutrino son creados instantáneamente en el mismo punto del espacio.
En 1957 la teoría de Fermi quedo establecida al solucionar algunos cabos sueltos, como la manera en que depende esta fuerza de las orientaciones relativas de los espines de las partículas que intervienen en el proceso. Tras este gran avance parecía que la teoría estaba libre de anomalías y explicaba los experimentos, pero era insatisfactoria a nivel teórico.
En primer lugar la fuerza nuclear débil funcionaba muy bien para la radiación beta pero daba resultados infinitos al aplicarla a fenómenos más exóticos como el cálculo de la probabilidad de dispersión de un neutrino por un antineutrino con el que colisiona. Sin embargo, a diferencia de la electrodinámica cuántica, parecía que esta teoría no era renormalizable.
Otro punto insatisfactorio era que incluía un gran número de elementos arbitrarios. Esta teoría podía ser muy diferente sin violar ningún principio físico conocido.
En 1967, Steven Weinberg desarrolló una base matemática para una teoría de la fuerza nuclear débil muy potente que posibilitaba una teoría de esta fuerza análoga a la electrodinámica cuántica. Igual que la fuerza electromagnética actúa mediante el intercambio de fotones, una fuerza débil no actuaría instantáneamente y en un único punto del espacio, sino que sería producida por el intercambio de bosones entre partículas distantes. Estos bosones debían tener masa porque sino ya se hubieran descubierto. Pero como operaban de manera tan similar al fotón en la electrodinámica cuántica que parecía que la teoría también sería renormalizable mediante redefinición de masas y otras magnitudes. Además esta teoría era muy determinada por sus principios subyacentes evitando la arbitrariedad.
Weinberg desarrolló un caso concreto de esta teoría en la que la de Fermi era una aproximación a bajas energías. Más allá de una analogía de la electrodinámica cuántica, esta teoría resultaba ser una teoría unificadora de las fuerzas nuclear débil y electromagnética, siendo ambas aspectos diferentes de la fuerza electrodébil. El fotón se unía a los bosones gauge débiles W± (responsables de la radiación beta) y Z° (responsable de un tipo neutro de fuera débil conocida como corriente neutra débil. La misma teoría en esencia fue desarrollada independientemente por Abdus Salam y Sheldon Glashow en 1968.
Tanto Weinberg como Salam creían que esta teoría era renormalizable pero no fueron capaces de demostrarlo. Fue Gerard t'Hooft en 1971 quien lo consiguió utilizando un novedoso método matemático desarrollado por Feynman. A partir de este momento y del descubrimiento en 1973 de las corrientes neutras en experimentos de dispersión de neutrinos la teoría electrodébil empezó a ser considerada seriamente gracias también a su consistencia y rigidez interna.
Además de predecir las corrientes neutras, la teoría electrodébil también predecía correctamente todas las propiedades de la fuerza débil y electromagnética que eran explicadas por la teoría de Fermi. Estas retrodicciones tenían valor porque la teoría de Fermi las explicaba con muchos elementos arbitrarios mientras que la teoría electrodébil lo hacía de una manera que no dejaba lugar a dudas. Es similar a lo que ocurría con la relatividad general respecto a la teoría de Newton.
Las verificaciones más espectaculares de la teoría electrodébil fueron los experimentos llevados a cabo por el equipo de Carlo Rubbia en el CERN en 1983 con el descubrimiento de las partículas W y en 1984 con la partícula Z con las propiedades predichas por la teoría electrodébil.
Igual que con la Relatividad General o la electrodinámica cuántica, la teoría electrodébil tuvo un consenso a favor previo a la confirmación experimental debido a su belleza (simplicidad, inevitabilidad y consistencia interna).
Esta fuerza quedó de manifiesto por primera vez en el descubrimiento de la radiactividad por Henri Becquerel en 1896. La radiación beta origen de esta radiactividad consiste en que un neutrón se convierta en un protón a la vez que se crea un electrón y un antineutrino que son expulsados del núcleo. Este cambio de identidad de las partículas es algo que no está permitido por ninguna otra fuerza de las conocidas anteriormente.
La fuerza nuclear débil es la responsable de la desintegración beta en la que un neutrón se transforma en un protón más un electrón más un antineutrino
La fuerza nuclear débil es mucho menos intensa que las fuerzas electromagnética o nuclear fuerte. Esto queda de manifiesto en que es una fuerza lenta ya que cualquier proceso en el que interviene dura una centésima de segundo, cuando la nuclear fuerte necesita solo 10-24s. Otra característica peculiar es que presenta una asimetría izquierda-derecha o quiralidad.
En 1933 Enrico Fermi desarrolló una teoría de la fuerza nuclear débil en la que la fuerza no actúa a distancia, sino que el neutrón, el electrón y el antineutrino son creados instantáneamente en el mismo punto del espacio.
En 1957 la teoría de Fermi quedo establecida al solucionar algunos cabos sueltos, como la manera en que depende esta fuerza de las orientaciones relativas de los espines de las partículas que intervienen en el proceso. Tras este gran avance parecía que la teoría estaba libre de anomalías y explicaba los experimentos, pero era insatisfactoria a nivel teórico.
En primer lugar la fuerza nuclear débil funcionaba muy bien para la radiación beta pero daba resultados infinitos al aplicarla a fenómenos más exóticos como el cálculo de la probabilidad de dispersión de un neutrino por un antineutrino con el que colisiona. Sin embargo, a diferencia de la electrodinámica cuántica, parecía que esta teoría no era renormalizable.
Otro punto insatisfactorio era que incluía un gran número de elementos arbitrarios. Esta teoría podía ser muy diferente sin violar ningún principio físico conocido.
En 1967, Steven Weinberg desarrolló una base matemática para una teoría de la fuerza nuclear débil muy potente que posibilitaba una teoría de esta fuerza análoga a la electrodinámica cuántica. Igual que la fuerza electromagnética actúa mediante el intercambio de fotones, una fuerza débil no actuaría instantáneamente y en un único punto del espacio, sino que sería producida por el intercambio de bosones entre partículas distantes. Estos bosones debían tener masa porque sino ya se hubieran descubierto. Pero como operaban de manera tan similar al fotón en la electrodinámica cuántica que parecía que la teoría también sería renormalizable mediante redefinición de masas y otras magnitudes. Además esta teoría era muy determinada por sus principios subyacentes evitando la arbitrariedad.
Diagrama de Feynman de la desintegración beta en la que un quark down se convierte en un quark up emitiendo un bosón W- que luego se desintegra en un electrón y un antineutrino
Weinberg desarrolló un caso concreto de esta teoría en la que la de Fermi era una aproximación a bajas energías. Más allá de una analogía de la electrodinámica cuántica, esta teoría resultaba ser una teoría unificadora de las fuerzas nuclear débil y electromagnética, siendo ambas aspectos diferentes de la fuerza electrodébil. El fotón se unía a los bosones gauge débiles W± (responsables de la radiación beta) y Z° (responsable de un tipo neutro de fuera débil conocida como corriente neutra débil. La misma teoría en esencia fue desarrollada independientemente por Abdus Salam y Sheldon Glashow en 1968.
Diagramas de Feynman de corrientes neutras débiles en las que no hay intercambio de carga
Tanto Weinberg como Salam creían que esta teoría era renormalizable pero no fueron capaces de demostrarlo. Fue Gerard t'Hooft en 1971 quien lo consiguió utilizando un novedoso método matemático desarrollado por Feynman. A partir de este momento y del descubrimiento en 1973 de las corrientes neutras en experimentos de dispersión de neutrinos la teoría electrodébil empezó a ser considerada seriamente gracias también a su consistencia y rigidez interna.
Además de predecir las corrientes neutras, la teoría electrodébil también predecía correctamente todas las propiedades de la fuerza débil y electromagnética que eran explicadas por la teoría de Fermi. Estas retrodicciones tenían valor porque la teoría de Fermi las explicaba con muchos elementos arbitrarios mientras que la teoría electrodébil lo hacía de una manera que no dejaba lugar a dudas. Es similar a lo que ocurría con la relatividad general respecto a la teoría de Newton.
Las verificaciones más espectaculares de la teoría electrodébil fueron los experimentos llevados a cabo por el equipo de Carlo Rubbia en el CERN en 1983 con el descubrimiento de las partículas W y en 1984 con la partícula Z con las propiedades predichas por la teoría electrodébil.
Igual que con la Relatividad General o la electrodinámica cuántica, la teoría electrodébil tuvo un consenso a favor previo a la confirmación experimental debido a su belleza (simplicidad, inevitabilidad y consistencia interna).
Capítulo 6: La Belleza de las Teorías
En los físicos el sentido de la belleza es una guía útil para seleccionar ideas y teorías que nos ayudan a explicar la naturaleza.
No es importante para la belleza de una teoría el que sus ecuaciones tengan soluciones elegantes. Las ecuaciones de la Relatividad General resultan difíciles de resolver excepto en las situaciones más sencillas, pero esto no está en contra de la belleza de la teoría misma.
Según el autor, parte de la belleza de una teoría consiste en una simplicidad de ideas, no de la simplicidad de tipo mecánico que puede medirse contando ecuaciones o símbolos.
En la teoría de Newton existen 3 ecuaciones mientras que en la Relatividad General hay 14 (10 de campo y 4 de movimiento). Sin embargo es la teoría de la Relatividad General la que es más bella gracias en parte a la simplicidad de su idea central de equivalencia entre gravitación e inercia.
Otra cualidad de una teoría bella es la inevitabilidad. La teoría de Newton podría no seguir la ley de la inversa del cuadrado sin tener que modificarla sustancialmente. Sin embargo la relatividad debe seguir la ley de la inversa del cuadrado para no aplastar sus bases conceptuales.
El mismo sentido de inevitabilidad puede encontrarse en parte en el modelo estándar de partículas elementales. Ambas teorías tienen una característica común que les aporta parte de esta simplicidad e inevitabilidad: ambas obedecen a principios de simetría.
Un principio de simetría es simplemente una afirmación de que algo se ve igual desde varios puntos de vista, como por ejemplo una esfera o el espacio vacío. Pero lo realmente importante no son las simetrias de las cosas, sino las simetrías de las leyes o principios de invariancia. En general, las leyes de la naturaleza son simétricas o invariantes respecto a la traslación y la rotación espacial o a la traslación temporal. El principio de relatividad de la teoría de la relatividad también es una simetría de la naturaleza. Cualquier principio de simetría es a su vez un principio de simplicidad. Si estas simetrías de las leyes de la naturaleza son importantes en física clásica, su importancia es aún mayor en mecánica cuántica.
Un electrón es idéntico a cualquier otro salvo en su energía, momento y espín. Estas magnitudes son las que caracterizan las formas en que la función de onda responde a transformaciones de simetría. La materia pierde así su papel central en física.
Hoy día se acepta generalmente que la única forma de combinar los principios de la relatividad especial y la mecánica cuántica es a través de una teoría cuántica de campos o algo muy similar. Este es precisamente el tipo de rigidez lógica que da su belleza a una teoría realmente fundamental: la mecánica cuántica y la relatividad especial son casi incompatibles, y su reconciliación en la teoría cuántica de campos impone poderosas restricciones a la forma en que las partículas pueden interaccionar mutuamente.
Una de estas restricciones es que se difumina la diferencia entre campos y partículas. Todo son campos y las partículas son manifestaciones o excitaciones de los campos allí donde su energía es suficiente para crearlas. Y en el caso de las partículas virtuales, ni eso porque gracias al principio de incertidumbre pueden tomar prestada la energía del vacío durante un tiempo suficientemente pequeño. De hecho así funcionan las interacciones, mediante el inintercambio de partículas virtuales.
En el caso del campo electromagnético, la interacción entre dos electrones es debida al intercambio de fotones y la interacción entre un electrón y un fotón por el intercambio de electrones (campo electrónico). La distinción entre materia y fuerza deja de ser esencial porque las partículas de materia también pueden transmitir fuerzas.
Otra de estas restricciones es que la energía y el momento de los campos esta cuantizada. Por ejemplo, en el campo gravitatorio la energía es transportada por los gravitones.
Todas las teorías mencionadas hasta ahora solamente limitan los tipos de fuerzas y materia que una teoría puede contener: en sí mismas no requieren la existencia de ningún tipo particular de materia o fuerza. Los principios de simetría se han vuelto cruciales en las últimas décadas del siglo XX: hay principios de simetría que dictan la existencia misma de todas las fuerzas conocidas de la naturaleza.
El principio de simetría subyacente en la teoría de la relatividad general establece que todos los sistemas de referencia son equivalentes: las mismas leyes son válidas para todos los observadores independientemente de su movimiento. La simetría entre los diferentes sistemas de referencia requiere la existencia de la gravitación. Las diferencias aparentes entre las leyes son en realidad la existencia de un campo gravitatorio.
La simetría subyacente en la teoría electrodébil no es espacio-temporal sino que tiene que ver con la identidad de las partículas. En mecanica cuántica es posible tener una partícula que no es, por ejemplo, ni un electrón ni un neutrino hasta que no se mida una propiedad que las distinga como la carga eléctrica. En la teoría electrodébil, la forma de las leyes de la naturaleza permanece invariable si reemplazamos electrones y neutrinos por estados combinados de ambos.
Esta es la simetría que conecta las fuerzas electromagnéticas con las fuerzas nucleares débiles. El fotón y las partículas W± y Z aparecen en la teoría electrodébil como paquetes de energía de cuatro campos, campos que son requeridos por esta simetría de la teoría electrodébil de igual forma que el campo gravitatorio es requerido por las simetrías de la relatividad general.
Estas simetrías se denominan simetrías internas porque estan relacionadas con la naturaleza intrínseca de las partículas más que con su posición o movimiento. La invariancia de las leyes de la naturaleza bajo un grupo de tales transformaciones de simetría interna dependientes de la posición y el tiempo se denomina simetría local o gauge.
Es la simetría local entre diferentes sistemas de referencia en el espacio y en el tiempo lo que hace necesaria la gravitación y, análogamente, es una segunda simetría local entre electrones y neutrinos lo que hace necesaria la existencia del campo fotónico, del campo W y del campo Z.
Todavía existe una tercera simetría local exacta asociada con la propiedad interna de los quarks conocida como carga de color. Cada uno de los 6 tipos o sabores de quarks se da en tres colores: rojo, blanco y azul. Pues existe una simetría exacta de la naturaleza entre los diferentes colores. La fuerza entre un quark rojo y uno blanco es la misma que entre un quark blanco y uno azul, y la fuerza entre dos quarks rojos es la misma que entre dos quarks azules.
Pero esta simetría va más allá del mero intercambio de colores. En mecánica cuántica podemos considerar estados de un solo quark que no son ni exactamente rojos ni exactamente blancos ni exactamente azules. Las leyes de la naturaleza toman exactamente la mismisma forma si reemplazamos los quarks rojos, blanco y azul por quarks en tres combinaciones de estados apropiada.
En analogía con la relatividad general, el hecho de que las leyes de la naturaleza no se vean afectadas al variar de un lugar a otro y de un instante a otro hace necesario incluir en la teoría una familia de campos que interaccionan con los quarks, análogos al campo gravitatorio. Son ocho campos que se conocen como campos gluónicos. La teoría de tales fuerzas, la cromodinámica cuántica, es sencillamente la teoría de quarks y gluones que respeta esta simetría de color local. El modelo estándar de las partículas elementales consiste en la teoría electrodébil ccombinada com la cromodinámica cuántica.
No solo los principios de simetría dan una especie de rigidez o inevitabilidad a las teorías. Únicamente con estos principios la teoría electrodébil o la cromodinámica cuántica serían solo uno de los muchos tipos de teorías posibles. La restricción adicional que nos permite escoger nuestro modelo estándar sencillo de entre la variedad de teorías más complicadas que satisfacen los mismos principios de simetría es que sea renormalizable. Resulta que esta condición impone un alto grado de simplicidad a las ecuaciones de la teoría y, junto con las diversas simetrías locales, sigue un largo camino hasta dar una forma única a nuestro modelo estándar de las partículas elementales.
La rigidez, simplicidad e inevitabilidad que conducen a la belleza parecen no darse en el modelo estándar por la gran cantidad de parámetros ajustables arbitrariamente y en la aparente aleatoriedad de sus valores. Sin embargo lo importante es disponer de un conjunto sencillo de principios que explique por qué las partículas son las que son independientemente de su cantidad o de sus propiedades.
De forma extraña e inquietante, aunque la belleza de las teorías físicas está incorporada en estructuras matemáticas rígidas basadas en principios subyacentes simples, las estructuras que tienen este tipo de belleza tienden a sobrevivir incluso cuándo se descubre que los principios subyacentes están equivocados.
Un buen ejemplo es la teoría de Dirac del electrón con la que en 1928 obtuvo una versión relativista de la ecuación de Schrödinger en términos de ondas de partículas. Esta teoría predijo el espín del electrón y la antimateria.
Esta teoría era un ingrediente clave de la electrodinámica cuántica en los años 30 y 40. Pero hoy sabemos que el punto de vista de Dirac era equivocado pues el contexto adecuado para la reconciliación de la mecánica cuántica con la relatividad especial es el formalismo conocido como teoría cuántica de campos, presentada por Heisenberg y Pauli en 1929 donde todas las partículas son cuantos de su campo asociado.
Casi por accidente la teoría de Dirac daba los mismos resultados que la teoría cuántica de campos para procesos que sólo involucran fotones, electrones y positrones. Pero la teoría cuántica de campos es más general: puede explicar por ejemplo la desintegración beta. En la teoría de Dirac los electrones son eternos y la creación de un par electrón-positrón se explica como el ascenso de un electrón de energía negativa a un estado de energía positiva dejando un hueco en el mar de electrones de energía negativa que es observado como un positrón. La aniquilación de un electrón y un positrón se interpreta como la caida de un electrón en un hueco. Sin embargo, en la desintegración beta se crean electrones sin positrones a partir de la energía y de la carga de vacío.
Por otro lado no hay nada en las teorías cuánticas de campos que requiera que las partículas tengan un espín concreto. El electrón resulta tener el espín que la teoría de Dirac requería, pero existen otras partículas con otros espines que, a su vez, tienen antipartículas y esto no tiene nada que ver con las energías negativas sobre las que especuló Dirac. Pese a todo, las matemáticas de la teoría de Dirac han sobrevivido como una parte esencial de la teoría cuántica de campos. Así la estructura formal de la teoría de Dirac ha sobrevivido a la muerte de los principios de la mecánica cuántica relativista que siguió Dirac para llegar a su teoría. Algo similar sucedió con el modelo de Bohr. Sus principios subyacentes han sido abandonados, pero aún utilizamos algo de su lenguaje y métodos de cálculo. Es curioso como algunas estructuras matemáticas bellas pueden ser trasladadas de un marco conceptual a otro. Como si la belleza fuera algo intrínseco o esencial del mundo esperando los principios adecuados que debe describir.
Otro ejemplo es la bella geometría riemanniana desarrollada exclusivamente por motivaciones matemáticas desconociendo sus aplicaciones físicas. Su belleza era de nuevo la de la inevitabilidad. Posteriormente la Relatividad General la ha tomado como la estructura matemática que la describe perfectamente.
Un ejemplo aún más extraño lo proporciona la historia de los principios de simetría interna. En física estos principios imponen típicamente una estructura de familias en la lista de partículas posibles. Estas transformaciones contínuas de simetría actúan sobre la etiqueta de las partículas de un modo que es matemáticamente equivalente a la forma en que las rotaciones ordinarias en tres dimensiones actúan sobre los espines de las partículas como protones, neutrones o electrones transformándolas en partículas que son combinaciones de varias de ellas con probabilidades arbitrarias de ser un protón, un neutrón o un electrón.
Por ello hasta los años 60 muchos físicos creyeron que las transformaciones de simetría interna que dejan invariantes las leyes de la naturaleza debían ser rotaciones en un cierto espacio de dos, tres o más dimensiones. Al descubrirse nuevas partículas a finales de los años cincuenta se tuvieron que introducir otros tipos de simetría interna. En 1960 los físicos teóricos se llevaron la grata sorpresa de que los matemáticos ya habían catalogado todas las simetrías posibles. El conjunto completo de transformaciones que deja inalterada cualquier cosa, ya sea un objeto específico o las leyes de la naturaleza, constituye una estructura matemática conocida como grupo y la matemática general de las transformaciones de simetría es conocida como teoría de grupos. La lista de los tipos de familias permitidas por cualquier simetría particular de las leyes de la naturaleza esta completamente determinada por la estructura matemática del grupo de simetría.
Las transformaciones que actuan de forma continua, como las rotaciones en el espacio ordinario o la combinación de electrones y neutrinos en la teoría electrodébil, se denominan grupos de Lie. Existen unos grupos de Lie simples a partir de los cuales pueden construirse todos los demás combinando sus transformaciones. En 1960 Gell-Mann descubrió que uno de estos grupos de Lie simples SU(3) era exactamente el necesario para imponer a la multitud de partículas elementales una estructura de familias similar a la que se había descubierto experimentalmente. Uno de los grandes éxitos de la nueva simetría SU(3) fue predecir una nueva partícula para completar una de las familias que fue descubierta con la masa predicha.
Aunque todavía no tenemos una idea segura de si en física fundamental podemos confiar en nuestro sentido de la belleza, en fisica de partículas elementales los juicios estéticos parecen estar trabajando cada vez mejor. Esto podría ser una evidencia de que vamos en la buena dirección y de que quizás no estamos demasiado lejos de nuestro objetivo.
7 Contra la filosofía
En este capítulo el autor se pregunta si la filosofía puede proporcionar a los físicos una guía hacia la teoría final de igual modo que los juicios estéticos. La opinión del autor es un rotundo no. Ni siquiera la filosofía de la ciencia a la que considera, como mucho, una recopilación agradable sobre la historia y los descubrimientos de la ciencia.
Aunque el autor valora obras de autores como Wittgenstein o Paul Feyerabend, considera que tienen poco que ver con el trabajo de la ciencia.
Wigner hablaba de la «irrazonable efectividad» de la matemática. Para el autor también se da la irrazonable inefectividad de la filosofía.
La doctrina del mecanicismo proporcionó mas molestia que utilidad debido al tiempo en que se perpetuó. Fue un antídoto al culto de los dioses y demonios en la antigua grecia. Fue ampliamente utilizada por Descartes, lo que a su vez influyó en Newton. El mecanicismo estaba tan arraigado que la idea de la gravitación de Newton con la acción a distancia tardó mucho en arraigar y fue gracias a filósofos como Kant y Voltaire. El único aspecto positivo de la filosofía es liberar a la ciencia de prejuicios filosóficos.
Incluso la teoría del campo electromagnético de Faraday y Maxwell fue originalmente formulado de manera mecanicista mediante el éter. La tradición mecanicista no fue definitivamente superada hasta el año 1905 con la relatividad especial.
Aún así en física de partículas se conservaba la distinción, de reminiscencia mecanicista, entre partículas de materia y mediadoras de fuerzas. Finalmente la teoría cuántica de campos formulada por Heisenberg y Pauli en 1929 eliminó esta separación: solo hay campos.
No sabemos si la clave de las teorías futuras estará en la partícula última de materia o en la unificación final de todas las fuerzas. Tampoco sabemos si esas son las preguntas correctas. Parece poco probable la resurrección del mecanicismo o el tener que volver a un dualismo de partículas y campos. Pero ni siquiera la teoría cuántica de campos es segura pues existen dificultades para incluir en ellas la gravitación. Probablemente no sepamos las preguntas correctas hasta estar cerca de las respuestas.
Aparte del mecanicismo, hay otras presuposiciones metafísicas que continúan molestando a la física, especialmente aquellas que tienen que ver con el espacio y el tiempo.
Kant enseñaba que el espacio y el tiempo no son parte de la realidad externa sino que más bien son estructuras preexistentes en nuestras mentes y que podíamos aprender sobre ellos mediante la razón pura. Para un kantiano era muy sorprendente que el espacio y el tiempo se pudiera ver afectado por el movimiento y la gravitación, fenómenos ajenos a la razón y por tanto no comprensibles por esta únicamente.
El tiempo no es eterno y puede no haber existido eternamente. Si el tiempo se creó en el Big Bang no tiene sentido preguntarse qué había antes. San Agustín en sus confesiones llegó a la conclusión de que Dios, que está fuera del tiempo, creó el tiempo junto al universo.
Hay teorías basadas en el universo inflacionario de un multiverso infinitamente viejo en el que nuestro universo en expansión es solo uno de las infinitos universos burbuja que contiene. Sobre la base del entendimiento puro no es posible concluir si el tiempo tiene una edad finita o no.

Modelo del Big Bang con una primera fase inflacionaria
La doctrina epistemológica del positivismo también puede ser un freno al avance científico. Esta doctrina demanda no solo que la ciencia deba contrastar sus teorías frente a la observación, sino que todo aspecto de nuestras teorías debe en todo punto referirse a magnitudes observables.
Ernst Mach es considerado como la persona que introdujo el positivismo en la física y para quién esta doctrina sirvió de antídoto a la metafísica de Kant. Físico y filosofo de Viena, influenció a Einstein cuya relatividad especial está llena de observadores y relojes. También influenció a Heisenberg en el Principio de Incertidumbre y alejando de la mecánica cuántica (basada hasta entonces en el modelo de Bohr) magnitudes inobservables como la posición y la velocidad, sustituidas por la energía y los ritmos de transición.
Pero el positivismo ha hecho tanto daño como bien, por ejemplo, dificultando la aceptación de la teoría atómica de Dalton y Avogadro y de la exitosa mecánica estadística de Maxwell, Boltzmann y Gibbs al considerar que los átomos no pueden ser observados.
El positivismo también jugó un papel oscurecedor en el problema de los infinitos de la electrodinámica cuántica retrasando su solución mediante una cuidadosa definición de la masa y la carga del electrón.
También en las teorías cuánticas de campos el positivismo fue negativo al intentar calcular la matriz S de scattering (dispersión) solo mediante magnitudes observables excluyendo los campos cuánticos, lo cuál era mucho más complicado. La matriz S es la tabla de probabilidades de todos los resultados posibles de todas las colisiones posibles entre partículas. Esta matriz resume todo lo que es realmente observable en las reacciones que involucran cualquier número de partículas. Su origen se remonta al trabajo de Heisenberg y Wheeler en los años 30 y 40.
El abandono más espectacular de los principios del positivismo se ha producido en el desarrollo de la teoría actual de los quarks, la cromodinámica cuántica. En esta teoría se da la propiedad de la libertad asintótica, que impide cualquier proceso en el que un quark pueda quedar aislado. Esta propiedad se da en algunas teorías cuánticas de campos (teorías gauge no abelianas o de Yang-Mills) como mostraron en 1973 David Gross, Frank Wilczek y David Politzer y consiste en que las fuerzas en dichas teorías decrecen a altas energías. La libertad asintótica y el hecho de que los gluones tengan masa nula hace que estos y los quarks no puedan ser observados. La razón está en que el intercambio de gluones sin masa entre quarks y gluones producen fuerzas de largo alcance que impiden tirar de ellos para dejarlos sueltos. La cromodinámica cuántica gobierna pues partículas no observables, justo al contrario de lo que requiere el positivismo.
8. Blues del siglo XX
Si el modelo estándar tiene gran poder predictivo, ¿por qué los físicos teóricos están tan tristes?
Los motivos son varios:
- El modelo estándar describe únicamente tres de las cuatro fuerzas conocidas dejando fuera la gravedad. Existen grandes obstáculos matemáticos para incorporarla en las teorías cuánticas de campos.
- La fuerza nuclear fuerte aparece de una forma bastante diferente de las fuerzas electromagnética y debil.
- Aunque el modelo estándar trata de forma unificada las fuerzas electromagnética y débil, existen diferencias obvias entre ambas como, por ejemplo, en su intensidad.
Muchas características del modelo estándar no están dictadas por principios fundamentales, sino que deben ser tomadas de la experiencia. Estas características aparentemente arbitrarias incluyen:
- una lista de partículas.
- ciertas constantes numéricas como las razones entre sus masas.
- las propias simetrías.
Por todo ello el modelo estándar claramente no es la respuesta final. Todos estos problemas del modelo estándar tienen que ver con la ruptura espontánea de simetría. El descubrimiento de este fenómeno ha sido uno de los grandes desarrollos liberadores de la ciencia del siglo XX. Su mayor éxito fue la explicación de las diferencias entre la fuerza electromagnética y la fuerza nuclear débil.
La teoría electrodébil está basada en un principio de simetría exacta, que dice que las leyes de la naturaleza son invariantes si en sus ecuaciones reemplazamos los campos del electrón y del neutrino por campos combinados de ambos, y al mismo tiempo combinamos análogamente los campos de las otras familias de partículas como el quark up y el quark down. Este principio de simetría es local porque estas combinaciones pueden variar con la posición y el tiempo.
Los campos del fotón y de los bosones W± y Z son una familia de campos cuya existencia viene dictada por una simetría similar a la que el campo gravitatorio viene impuesto por la simetría entre diferentes sistemas de coordenadas. Estos campos también deberían combinarse entre sí al combinar los campos del electrón y del neutrino y los campos de los quarks. Por eso la simetría entre electrones y neutrinos es también una simetría entre las fuerzas electromagnética y nuclear débil.
Acoplamiento entre los tres bosones gauge débiles
Esta simetría es una propiedad de las ecuaciones subyacentes en el modelo estándar, pero esta simetría no es satisfecha por las soluciones de dichas ecuaciones, es decir, por las propiedades de las propias partículas. Por eso los bosones W± y Z tienen masa pero el fotón no. Igual pasa con el electrón y el neutrino. Las masas concretas de estas partículas son una situación particular de las ecuaciones. La simetría de las ecuaciones no está necesariamente reflejada en cada solución individual de dichas ecuaciones, sino solo en el conjunto total de todas las soluciones de las ecuaciones. La naturaleza tal como la conocemos es sólo una solución de todas las ecuaciones del modelo estándar, y no supone ninguna diferencia qué solución sea con tal de que todas las diferentes soluciones estén relacionadas mediante principios de simetría exacta.
En tales casos decimos que la simetría está rota. Llamamos a este fenómeno una ruptura espontánea de simetría porque nada rompe la simetría en las ecuaciones de la teoría. La ruptura de simetría aparece espontáneamente en las diversas soluciones de estas ecuaciones. Hay mas simetría y belleza en las leyes de la naturaleza de lo que parece por simple observación. Un ejemplo de simetría rota es un imán, que por debajo de 770° desarrolla un campo magnético en cierta dirección aunque las ecuaciones que lo gobiernan son espacialmente simétricas.
En el caso de la teoría electrodébil existe una ruptura espontánea de simetría que se manifiesta en una diferencia de masa entre el fotón y los bosones W± y Z que a su vez hace que la intensidad y el alcance de ambas difiera.
La ruptura espontánea de simetría de la fuerza electrodébil se debe a la presencia de un campo cuyo valor de vacío es no nulo. Es este valor diferente de cero lo que hace que la simetría se rompa. Como todos los campos cuánticos, la energía y el momento de este nuevo campo viene en paquetes, el bosón de Higgs.
A la izquierda el potencial de Higgs es nulo cuando el campo de Higgs también lo es. Sin embargo a la derecha se rompe esta simetría y el potencial es diferente de cero cuando el campo de Higgs es nulo
Con la inclusión del campo de Higgs todas las partículas tienen masa nula salvo el bosón de Higgs, cuya masa es la única que aparece en el modelo estándar. Todas las demás partículas adquieren una masa proporcional al bosón de Higgs mediante el mecanismo de ruptura espontánea de la simetría electrodébil. Por tanto conocer el origen de la masa sería equivalente a entender el mecanismo de ruptura espontánea de simetría. Es posible que en el origen del universo la simetría electrodébil no estuviera rota, y que se rompiera pocos instantes después al bajar la temperatura de un umbral.
El concepto de ruptura espontánea de simetría también se ha utilizado para intentar incluir la fuerza nuclear fuerte dentro del mismo marco unificado que las fuerzas débil y electromagnética. Sin embargo no existe una simetría en las ecuaciones del modelo estándar que relacionen las fuerzas nucleares fuertes con la débil y la electromagnética. Desde los 70 se buscó una teoría subyacente al modelo estándar en que las tres interacciones quedaran unificadas mediante un único y gran grupo de simetrías espontáneamente rotas como SU(5).
Un obstáculo obvio de estas teorías es la diferencia entre las intensidades intrínsecas entre las tres fuerzas. Estas intensidades determinan las fuerzas junto a la masa de la partícula mediadora y caracterizan la probabilidad de que partículas como los fotones, gluones, W± o Z sean emitidas y reabsorbidas en las reacciones entre partículas. La simetría exigiría que estas tres intensidades fueran iguales cosa que no sucede en la realidad ni aunque fuera debido a una simetría rota.
Una posible solución sería que las intensidades de las tres fuerzas se igualaran a una energía extremadamente alta mucho mayor que la alcanzable con los experimentos actuales, una centésima parte de la energía de Planck. La energía debe ser elevada porque la intensidad intrínseca de la fuerza nuclear fuerte desciende muy lentamente con la energía. Además, a la energía de Planck la fuerza gravitatoria se haría tan intensa como el resto de fuerzas unificándose con ellas.
El hecho de que la energía de unificación electrodébil y fuerte y la energía de Planck estén próximas sugiere que la ruptura de cualquier simetría que una las fuerzas fuerte y electrodébil es solo parte de una ruptura de simetría más fundamental: la ruptura de cualquier simetría que relacione la gravitación con las demás fuerzas de la naturaleza. Podría existir una teoría unificada que englobe las cuatro fuerzas de la naturaleza conocidas.
Por desgracia, la razón de que la gravitación quede fuera del modelo estándar es que resulta muy difícil describir la gravitación en el lenguaje de la teoría cuántica de campos. Podemos aplicar simplemente las reglas de la mecánica cuántica a las ecuaciones de campo de la relatividad general, pero entonces entramos en el viejo problema de los infinitos. Por ejemplo se obtienen probabilidades infinitas en lo que sucede en colisiones de dos gravitones que intercambian más de un gravitón.
El valor tan elevado de la energía de Planck nos enfrenta a otro gran problema. Esta energía surge en un nivel tan profundo que podemos suponer que es la unidad fundamental de energía que aparece en las ecuaciones de la teoría final. El misterio está en por qué todas las demás energías son tan pequeñas. La masa del bosón de Higgs se estima 100 billones de veces más pequeña que la energía de Planck. Esto significa que hay una jerarquía de simetrías: cualquiera que sea la simetría que unifica las fuerzas gravitatoria y nuclear fuerte con las fuerzas electrodébiles se rompe aproximadamente 100 billones de veces más fuertemente que la simetría que unifica las interacciones débiles y electromagnéticas. Esto se conoce como el problema de la jerarquía.
Una aproximación a este problema se basa en la supersimetría, una nueva simetría que relaciona partículas de diferente espín de modo que forman nuevas «superfamilias». En estas teorías la masa del bosón de Higgs sería nula en las ecuaciones fundamentales de la teoría y aparecería a partir de un complicado mecanismo de ruptura de la supersimetría.
Más allá del problema de la jerarquía, la conjetura de que todas las fuerzas de la naturaleza se unificarán a una energía del orden de la energía de Planck ha arrojado una nueva luz sobre el problema de los infinitos. La condición de renormalización fue una poderosa guía para la construcción del modelo estándar. Pero como el modelo estándar deja fuera la gravitación, se cree que es simplemente una aproximación válida a baja energía a una teoría unificada realmente fundamental y que pierde su validez a energías como la energía de Planck. Por eso el problema de los infinitos no ha desaparecido, sino que es un problema para la teoría final, no para una aproximación a baja energía como parece ser el modelo estándar.
Podría ser que las ecuaciones del modelo estándar no son del tipo muy simple que sería renormalizable, sino que contienen cualquier término concebible consistente con las simetrías de la teoría. Estos nuevos términos no renormalizables aparecerían divididos por potencias de alguna cantidad del orden de la energía de Planck, que a bajas energías serían despreciables. La condición de renormalización era correcta a efectos prácticos aunque no lógicamente necesaria.
Estos nuevos términos hacen que algunas magnitudes no se conserven, como la del número de quarks o el número leptónico. La primera impide la desintegración del protón en un positrón y un fotón y garantizaría la estabilidad de la materia. La segunda hacía que el neutrino tuviera masa nula. Experimentos como el super Kamiokande de Japón han mostrado que los neutrinos tendrían una masa minúscula con lo que no se conservaría el número leptónico. Esto hace que el neutrino pueda mutar de un tipo a otro (electrónico, muónico y tau) y explicaría por qué históricamente siempre se había detectado menos neutrinos del primer tipo de los esperados procedentes del Sol.
9 La Forma de una teoría final
La mecánica cuántica es la única parte de la física actual que probablemente sobreviva sin cambios en una teoría final debido a su impresionante acuerdo con los experimentos y a la imposibilidad de cambiarla sin caer en absurdos lógicos.
La mecánica cuántica pone el escenario (vacío) y los principios de simetría son los que imponen el contenido. Las simetrías espacio-temporales de la relatividad especial exigen que el modelo estándar sea formulado como una teoría de campos, y las simetrías internas dictan la existencia del campo electromagnético y los otros campos portadores de fuerzas. La gravitación puede también ser entendida sobre la base de un principio de simetría: el principio de equivalencia.
Se supone, por tanto, que una teoría final reposará sobre principios de simetría que unifiquen la gravedad con las otras tres fuerzas. Sin embargo no se disponía de una teoría cuántica que incorporase consistente y necesariamente la simetría subyacente a la relatividad especial.
La teoría de cuerdas ha sido el primer candidato a teoría final al incorporar de manera consistente la relatividad general con la mecánica cuántica. En esta teoría la entidad física fundamental es un objeto unidimensional microscópico: una cuerda mecanocuántica relativista de una longitud de Planck de tamaño que vista a grandes distancias parece una partícula puntual. Cuando se desplazan por el espacio las cuerdas vibran y en cada posible modo de vibración da origen a una partícula diferente.
Las teorías de cuerdas más plausibles incorporan la supersimetría para solucionar probemas importantes. Por ello se llaman teorías de supercuerdas.
Incorpora necesariamente (sino sería inconsistente) el gravitón, una partícula de masa nula y espín 2. Desde los años sesenta se sabía que cualquier teoría que incorporara está partícula se parecería mucho a la relatividad general. Por tanto la teoría de cuerdas es una teoría de gravedad cuántica al incorporar también el resto de partículas conocidas.
Para dar a las fuerzas gravitatorias la intensidad correcta había que incrementar la tensión de las cuerdas en las ecuaciones básicas de la teoría de manera que la diferencia entre el estado de energía más bajo y el siguiente de una cuerda fuera del orden de la energía de Planck. Esto implica que todas las partículas del modelo estándar deben identificarse con los modos de vibración más bajos. De lo contrario, su energía (o masa) sería tan elevada que aún no se habrían descubierto.
Desde este punto de vista, una teoría cuántica de campos como el modelo estándar es una aproximación a baja energía a una teoría fundamental que no es en absoluto una teoría cuántica de campos, sino posiblemente una teoría de cuerdas. La naturaleza no se describe realmente mediante una teoría cuántica de campos, sino que cualquier teoría que satisfaga los requisitos de la mecánica cuántica y de la relatividad especial tiene el aspecto de una teoría cuántica de campos a bajas energías. El modelo estándar es una teoría cuántica de campos efectiva.
Las teorías de cuerdas podrían resolver el problema de los infinitos gracias a que las cuerdas no son puntuales como las partículas, sino que tienen extensión al ser unidimensionales. Esto evita infinitos por ejemplo con la ley inversa del cuadrado al colocar dos partículas en la misma posición.
El interés por las teorías de cuerdas empezó realmente en 1984 cuando Schwarz y Michael Green demostraron que dos teorías de cuerdas específicas estaban libres de anomalías. Y aumentó cuando se demostró que el límite a bajas energías de estas dos teorías tenía un gran parecido con el modelo estándar.
Actualmente hay miles de estas teorías todas ellas satisfaciendo la misma simetría subyacente, conocida como simetría conforme. Esta simetría no es empírica, sino que es necesaria para garantizar la consistencia mecanocuántica de las teorías.
Una diferencia importante entre las teorías de cuerdas y todas las teorías anteriores es que las simetrías espacio-temporales y las simetrías internas no están introducidas por la fuerza, sino que son consecuencias de la simetría conforme y como las reglas de la mecánica cuántica son satisfechas en cada teoría de cuerdas. Esto significaría un avance hacia una explicación racional de la naturaleza.
Una de las dificultades de las teorías de cuerdas es que no existe un criterio para seleccionar la teoría que se aplica al mundo real. Además la teoría no ha proporcionado predicciones comprobables con la tecnología actual.
Una posibilidad sería que nuestro universo fuera una de las muchas burbujas de un megaverso o multiverso, cada una con unas leyes de la naturaleza y unas constantes físicas diferentes.
Podría ser que finalmente encontráramos que las constantes de la naturaleza vienen determinadas por algún principio de simetría o de otra clase salvo una, la constante cosmológica. Esta constante representa una fuerza repulsiva y fue introducida por Einstein para compensar la atracción gravitatoria y así justificar un universo estático. Tras comprobarse que el universo se expande, actualmente su sentido físico sería el de una energía de vacío o energía oscura.
Esta energía de vacío sería originada por las fluctuaciones cuánticas permitidas por el principio de incertidumbre de la mecánica cuántica. Su existencia sería detectable solo por los efectos gravitatorios. Sin embargo los cálculos de esta energía mediante las teorías cuánticas de campos dan infinito o, descartando las contribuciones de alta energía, un valor 120 órdenes de magnitud mayor que el valor observado. Seguramente es la peor predicción de la historia de la física.
Podría ocurrir una cancelación de la energía repulsiva con una energia de vacio negativa aunque no tiene por qué ser una cancelación exacta. Por debajo de un límite permitiría que la expansión no fuera tan rápida como para impedir la formación de estrellas y galaxias por atracción gravitatoria. Sin embargo las mediciones actuales implican una cancelación hasta la 120 cifra decimal. Algo casi inverosímil.
Esta constante cosmológica o energía oscura no nula podría proporcionar la cantidad de materia-energía que falta para explicar la expansión actual del universo justo por encima del valor crítico. También explicaría su edad al disminuir la expansión inicial por una mayor densidad de energía.
Desafortunadamente la teoría de cuerdas tampoco aporta actualmente ninguna solución al problema del valor de la constante cosmológica.
No es seguro que exista una teoría última o final pero históricamente siempre se han ido descubriendo leyes más fundamentales que unificaban una o varias teorías existentes, como la ley de gravitación de Newton, el electromagnetismo o la teoría electrodébil.
Además teorías como la mecánica cuántica nos indican que hay un orden en la naturaleza y nada impide por el momento que ese orden sea explicado por una única teoría fundamental en lugar de por varias teorías parciales. Las inconsistencias de la relatividad general en las singularidades de los agujeros negros o en el Big Bang y su incompatibilidad con la mecánica cuántica indica la existencia de, al menos, una teoría más profunda.
Lo que sí podría ocurrir es que no fuéramos lo suficientemente inteligentes como para descubrirlas. La opinión del autor es que existe una teoría final y que somos capaces de descubrirla.
La teoría final no sería lógicamente inevitable porque hay otras teorías que aunque no sean totalmente correctas no son inconsistentes lógicamente. Es lo que sucede con las leyes de Newton respecto a la mecánica cuántica. Esta última es lógicamente independiente porque no es modificable fácilmente sin llegar a absurdos lógicos.
En una teoría lógicamente independiente cualquier constante de la naturaleza podría calcularse a partir de primeros principios. Un pequeño cambio en el valor de cualquier constante destruiría la consistencia de la teoría.
En todo caso el descubrimiento de una teoría final no sería el final de la empresa de la ciencia. Es posible que al principio no supiéramos resolver sus ecuaciones más que en unos pocos casos sencillos con lo que habría que desarrollar nuevos métodos matemáticos. Quedarían problemas de ingeniería por resolver y también cuestiones médicas como la conciencia o la memoria y nuevas enfermedades que curar.
Conocer la teoría final sería como alcanzar la «mente de Dios», tal y como se refirió Stephen Hawking a las leyes de la naturaleza en su libro Historia del Tiempo. Conociendo estas leyes podríamos tener alguna intuición sobre la obra de Dios.
Podemos preguntarnos si encontraremos en las leyes finales de la naturaleza un Dios creador. Es una pregunta que roza el absurdo porque es dificil imaginar que algún día podamos estar en posesión de los principios últimos que no necesitan más explicación.
Lo que muestra la historia de la ciencia es que no lo encontraremos a ese Dios. La ciencia parece negar la existencia de Dios primero con la desmitificación de los cielos gracias a Copernico, Galileo, Bruno y Newton. Y luego con el descubrimiento de Hubble de que nuestra galaxia es una entre tantas. También la vida ha sido desmitificada con el hecho de que con agua, hidrógeno, oxígeno, carbono y energía las substancias orgánicas básicas para la vida pueden generarse espontáneamente. La teoría de la evolución de Darwin también hace prescindible un Dios creador.
Sin embargo, el ajuste de las constantes de la naturaleza parece perfecto para la aparición de la vida tal y como la conocemos. Ligeras modificaciones en estas constantes haría que no se hubieran podido crear las estrellas, las fábricas de los elementos indispensables para la vida. Esto haría pensar en la intervención de un ser creador, pero en las teorías modernas de universos paralelos estas constantes pueden cambiar de una región a otra. Por tanto podría ocurrir que habitáramos una de ellas cuyas constantes fundamentales son aquellas que permiten la vida.
En 1988 se anunció que Ellis County en Texas sería la sede del mayor y más costoso instrumento científico del mundo, el Supercolisionador Superconductor o SSC por sus siglas en inglés.
Su objetivo era descubrir el bosón de Higgs o bien nuevas fuerzas extrafuertes que expliquen la ruptura espontánea de simetría de la fuerza electrodébil y den consistencia interna al modelo estándar: la simetría exacta en la forma en que ambas fuerzas entran en las ecuaciones de la teoría que no está presente en las soluciones, es decir, en las propiedades de las partículas y las fuerzas.
Para ello este acelerador de partículas tendría una longitud de 85km por la que se acelerarían dos haces de protones en sentidos opuestos hasta los 20TeV. Para ello se utilizarían más de 3000 bobinas deflectoras, casi mil bobinas focalizadoras, miles de kilómetros de cable superconductor enfriados con millones de litros de helio líquido.
Aunque este acelerador de partículas estaba pensado para confirmar la ruptura espontánea de simetría de la fuerza electrodébil y descubrir más sobre el mecanismo físico con el que se produce, la historia muestra que estos experimentos siempre han descubierto cosas no esperadas además de aquellas para las que fueron diseñados. Algunos ejemplos son:
En el Supercolisionador Superconductor se hubieran podido descubrir las compañeras supersimétricas de las partículas conocidas, descubrir que los quarks no son partículas elementales, nuevas fuerzas consecuencia de nuevas simetrías internas u obtenido más información acerca de la materia oscura, uno de los grandes enigmas de la física actual.
La materia oscura no puede ser materia ordinaria porque entonces las predicciones del modelo del Big Bang de producción de estas partículas en los primeros minutos de la expansión del universo no estarían de acuerdo con la observación tal y como lo están.
Si en los aceleradores encontráramos nuevas partículas estables y pudiéramos medir sus propiedades, entonces podríamos calcular su ritmo de producción en el universo primitivo y decidir si constituye toda la materia oscura que falta para explicar el ritmo actual de expansión del universo.
El satélite COBE ha estudiado irregularidades del fondo cósmico de microondas de cuando el universo tenía 300.000 años. En ese momento se hizo transparente a la radiación (de fotones) al ser los electrones capturados por los núcleos formando átomos neutros. Estas irregularidades no se podían deber a galaxias jóvenes en formación pues eran iirregularidades muy grandes de zonas que ya habían comenzado el colapso gravitatorio. Esta materia no podía ser la ordinaria porque las inhomogeneidades de esta materia no podía haber experimentado ningún crecimiento significativo hasta que el universo se hubiera hecho transparente a la radiación. La presión existente de la propia radiación hubiera dispersado cualquier acumulación de materia.
Sin embargo la materia oscura exótica que está compuesta de partículas eléctricamente neutras se habría hecho transparente a la radiación mucho antes, y así hubiera comenzado su condensación gravitatoria mucho más cerca del principio, produciendo inhomogeneidades a escalas galácticas mucho mayores, quizás suficientes para haber crecido hasta las galaxias actuales.
Además estos grandes experimentos de tecnología punta como los aceleradores son como una especie de locomotora industrial que obligua a avances en diversas tecnologías cruciales: criogenia, diseño de bobinas, computación en tiempo real. Es también un recurso intelectual para retener el talento.
Nadie sabe si un acelerador nos permitirá dar un último paso hacia la teoría final. Para el autor estas máquinas son los continuadores necesarios de una progresión histórica de los grandes instrumentos científicos, que se remontan mucho tiempo antes de los aceleradores actuales de Brookhaven, el CERN, DESY, Fermilab, KEK y SLAC hasta el ciclotrón de Lawrence y el tubo de rayos catódicos de Thomson y, mucho más atrás, hasta el espectroscopio de Frauenhofer y el telescopio de Galileo. Se descubran o no las leyes de la naturaleza, supone algo grande para nosotros continuar la tradición de someter la naturaleza a examen, de preguntar una y otra vez por qué es como es.
Sin embargo el proyecto del SSC fue cancelado el 1993 por motivos políticos.
En este libro se plantea la razonable hipótesis de que exista una teoría final y fundamental porque la historia nos muestra que nuestras teorías cada vez son más fundamentales y se apoyan en cada vez menos principios básicos. Gracias también a nuestra experiencia con las teorías actuales más exitosas, este teoría final debería apoyarse en principios de simetría que le dieran una rigidez e inevitabilidad lógica, además de simplicidad. Simplicidad, inevitabilidad lógica y consistencia interna es lo que dan belleza a las teorías. Y se espera que la teoría final sea bella. Una posible candidata a teoría final es la teoría de supercuerdas, aunque actualmente está atravesando un período de dificultades.
En los primeros capítulos se repasa la mecánica cuántica y tres de las teorías más existosas y bellas de la física: la relatividad general, la electrodinámica cuántica y la teoría electrodébil. Las tres están basadas en principios de simetría y han sido y son confirmadas por los experimentos hasta un gran nivel de precisión. La mecánica cuántica es también una teoría en excelente acuerdo con la observación, pero existe un cierto descontento y desconcierto por el hecho de que solo permita calcular probabilidades y sobre lo que ocurre en el momento de la medición. La interpretación de Copenhague es operativa pero no acaba de resultar satisfactoria.
Lo que más me ha gustado de este libro es descubrir hasta que punto las teorías actuales de la física están basadas en principios de simetría que implican la aparición de ciertas interacciones o fuerzas. Estos principios de simetría proporcionan una inevitabilidad y simplicidad a las teorías que las hace bellas.
En este sentido, se espera que la teoría final posea un gran número de simetrías que determinen las interacciones y que le aporten una rigidez lógica, inevitabilidad y simplicidad que la hagan bella y elegante. De la física actual, se considera que únicamente la mecánica cuántica será incorporada por la teoría final prácticamente sin modificaciones, pues no se ha conseguido modificarla minimamente sin llegar a absurdos lógicos o sin dejar de realizar predicciones acertadas.
Las teorías de cuerdas más plausibles incorporan la supersimetría para solucionar probemas importantes. Por ello se llaman teorías de supercuerdas.
Los bosones y sus posibles compañeras supersimétricas
Los fermiones, las partículas que constituyen la materia, y sus posibles supercompañeras
Incorpora necesariamente (sino sería inconsistente) el gravitón, una partícula de masa nula y espín 2. Desde los años sesenta se sabía que cualquier teoría que incorporara está partícula se parecería mucho a la relatividad general. Por tanto la teoría de cuerdas es una teoría de gravedad cuántica al incorporar también el resto de partículas conocidas.
Para dar a las fuerzas gravitatorias la intensidad correcta había que incrementar la tensión de las cuerdas en las ecuaciones básicas de la teoría de manera que la diferencia entre el estado de energía más bajo y el siguiente de una cuerda fuera del orden de la energía de Planck. Esto implica que todas las partículas del modelo estándar deben identificarse con los modos de vibración más bajos. De lo contrario, su energía (o masa) sería tan elevada que aún no se habrían descubierto.
Energía de Planck obtenida a partir de la masa de Planck y la equivalencia entre masa y energía de la Relatividad Especial
Desde este punto de vista, una teoría cuántica de campos como el modelo estándar es una aproximación a baja energía a una teoría fundamental que no es en absoluto una teoría cuántica de campos, sino posiblemente una teoría de cuerdas. La naturaleza no se describe realmente mediante una teoría cuántica de campos, sino que cualquier teoría que satisfaga los requisitos de la mecánica cuántica y de la relatividad especial tiene el aspecto de una teoría cuántica de campos a bajas energías. El modelo estándar es una teoría cuántica de campos efectiva.
Las teorías de cuerdas podrían resolver el problema de los infinitos gracias a que las cuerdas no son puntuales como las partículas, sino que tienen extensión al ser unidimensionales. Esto evita infinitos por ejemplo con la ley inversa del cuadrado al colocar dos partículas en la misma posición.
Las cuerdas tienen una longitud en la escala de Planck
El interés por las teorías de cuerdas empezó realmente en 1984 cuando Schwarz y Michael Green demostraron que dos teorías de cuerdas específicas estaban libres de anomalías. Y aumentó cuando se demostró que el límite a bajas energías de estas dos teorías tenía un gran parecido con el modelo estándar.
Actualmente hay miles de estas teorías todas ellas satisfaciendo la misma simetría subyacente, conocida como simetría conforme. Esta simetría no es empírica, sino que es necesaria para garantizar la consistencia mecanocuántica de las teorías.
Una diferencia importante entre las teorías de cuerdas y todas las teorías anteriores es que las simetrías espacio-temporales y las simetrías internas no están introducidas por la fuerza, sino que son consecuencias de la simetría conforme y como las reglas de la mecánica cuántica son satisfechas en cada teoría de cuerdas. Esto significaría un avance hacia una explicación racional de la naturaleza.
Una de las dificultades de las teorías de cuerdas es que no existe un criterio para seleccionar la teoría que se aplica al mundo real. Además la teoría no ha proporcionado predicciones comprobables con la tecnología actual.
Las dualidades debil-fuerte y radio grande-pequeño crean una red de conexiones que interrelacionan y fusionan las cinco teorías de cuerdas, la supergravedad en once dimensiones y la Teoría M en un marco unificado.
Una posibilidad sería que nuestro universo fuera una de las muchas burbujas de un megaverso o multiverso, cada una con unas leyes de la naturaleza y unas constantes físicas diferentes.
Podría ser que finalmente encontráramos que las constantes de la naturaleza vienen determinadas por algún principio de simetría o de otra clase salvo una, la constante cosmológica. Esta constante representa una fuerza repulsiva y fue introducida por Einstein para compensar la atracción gravitatoria y así justificar un universo estático. Tras comprobarse que el universo se expande, actualmente su sentido físico sería el de una energía de vacío o energía oscura.
Esta energía de vacío sería originada por las fluctuaciones cuánticas permitidas por el principio de incertidumbre de la mecánica cuántica. Su existencia sería detectable solo por los efectos gravitatorios. Sin embargo los cálculos de esta energía mediante las teorías cuánticas de campos dan infinito o, descartando las contribuciones de alta energía, un valor 120 órdenes de magnitud mayor que el valor observado. Seguramente es la peor predicción de la historia de la física.
Podría ocurrir una cancelación de la energía repulsiva con una energia de vacio negativa aunque no tiene por qué ser una cancelación exacta. Por debajo de un límite permitiría que la expansión no fuera tan rápida como para impedir la formación de estrellas y galaxias por atracción gravitatoria. Sin embargo las mediciones actuales implican una cancelación hasta la 120 cifra decimal. Algo casi inverosímil.
Esta constante cosmológica o energía oscura no nula podría proporcionar la cantidad de materia-energía que falta para explicar la expansión actual del universo justo por encima del valor crítico. También explicaría su edad al disminuir la expansión inicial por una mayor densidad de energía.
Desafortunadamente la teoría de cuerdas tampoco aporta actualmente ninguna solución al problema del valor de la constante cosmológica.
10. Frente a la finalidad
No es seguro que exista una teoría última o final pero históricamente siempre se han ido descubriendo leyes más fundamentales que unificaban una o varias teorías existentes, como la ley de gravitación de Newton, el electromagnetismo o la teoría electrodébil.
Además teorías como la mecánica cuántica nos indican que hay un orden en la naturaleza y nada impide por el momento que ese orden sea explicado por una única teoría fundamental en lugar de por varias teorías parciales. Las inconsistencias de la relatividad general en las singularidades de los agujeros negros o en el Big Bang y su incompatibilidad con la mecánica cuántica indica la existencia de, al menos, una teoría más profunda.
Tiempo de Planck en función de la constante de Planck, la constante de gravitación universal y la velocidad de la luz. Para tiempos inferiores en el inicio del universo la relatividad general y la mecánica cuántica deben ser reconciliadas con una teoría de gravedad cuántica
Lo que sí podría ocurrir es que no fuéramos lo suficientemente inteligentes como para descubrirlas. La opinión del autor es que existe una teoría final y que somos capaces de descubrirla.
La teoría final no sería lógicamente inevitable porque hay otras teorías que aunque no sean totalmente correctas no son inconsistentes lógicamente. Es lo que sucede con las leyes de Newton respecto a la mecánica cuántica. Esta última es lógicamente independiente porque no es modificable fácilmente sin llegar a absurdos lógicos.
En una teoría lógicamente independiente cualquier constante de la naturaleza podría calcularse a partir de primeros principios. Un pequeño cambio en el valor de cualquier constante destruiría la consistencia de la teoría.
En todo caso el descubrimiento de una teoría final no sería el final de la empresa de la ciencia. Es posible que al principio no supiéramos resolver sus ecuaciones más que en unos pocos casos sencillos con lo que habría que desarrollar nuevos métodos matemáticos. Quedarían problemas de ingeniería por resolver y también cuestiones médicas como la conciencia o la memoria y nuevas enfermedades que curar.
11. Y qué pasa con Dios?
Conocer la teoría final sería como alcanzar la «mente de Dios», tal y como se refirió Stephen Hawking a las leyes de la naturaleza en su libro Historia del Tiempo. Conociendo estas leyes podríamos tener alguna intuición sobre la obra de Dios.
Podemos preguntarnos si encontraremos en las leyes finales de la naturaleza un Dios creador. Es una pregunta que roza el absurdo porque es dificil imaginar que algún día podamos estar en posesión de los principios últimos que no necesitan más explicación.
Lo que muestra la historia de la ciencia es que no lo encontraremos a ese Dios. La ciencia parece negar la existencia de Dios primero con la desmitificación de los cielos gracias a Copernico, Galileo, Bruno y Newton. Y luego con el descubrimiento de Hubble de que nuestra galaxia es una entre tantas. También la vida ha sido desmitificada con el hecho de que con agua, hidrógeno, oxígeno, carbono y energía las substancias orgánicas básicas para la vida pueden generarse espontáneamente. La teoría de la evolución de Darwin también hace prescindible un Dios creador.
Sin embargo, el ajuste de las constantes de la naturaleza parece perfecto para la aparición de la vida tal y como la conocemos. Ligeras modificaciones en estas constantes haría que no se hubieran podido crear las estrellas, las fábricas de los elementos indispensables para la vida. Esto haría pensar en la intervención de un ser creador, pero en las teorías modernas de universos paralelos estas constantes pueden cambiar de una región a otra. Por tanto podría ocurrir que habitáramos una de ellas cuyas constantes fundamentales son aquellas que permiten la vida.
12. Ellis County, allá en el sur
En 1988 se anunció que Ellis County en Texas sería la sede del mayor y más costoso instrumento científico del mundo, el Supercolisionador Superconductor o SSC por sus siglas en inglés.
Su objetivo era descubrir el bosón de Higgs o bien nuevas fuerzas extrafuertes que expliquen la ruptura espontánea de simetría de la fuerza electrodébil y den consistencia interna al modelo estándar: la simetría exacta en la forma en que ambas fuerzas entran en las ecuaciones de la teoría que no está presente en las soluciones, es decir, en las propiedades de las partículas y las fuerzas.
Para ello este acelerador de partículas tendría una longitud de 85km por la que se acelerarían dos haces de protones en sentidos opuestos hasta los 20TeV. Para ello se utilizarían más de 3000 bobinas deflectoras, casi mil bobinas focalizadoras, miles de kilómetros de cable superconductor enfriados con millones de litros de helio líquido.
Aunque este acelerador de partículas estaba pensado para confirmar la ruptura espontánea de simetría de la fuerza electrodébil y descubrir más sobre el mecanismo físico con el que se produce, la historia muestra que estos experimentos siempre han descubierto cosas no esperadas además de aquellas para las que fueron diseñados. Algunos ejemplos son:
- En el Sincrotrón de Protones en el CERN utilizando haces de neutrinos se descubrieron las corrientes débiles neutras en 1973 que, lo que verificó la teoría electrodébil.
- En el colisionador electrón-positrón del CERN se descubrió la partícula Z°.
- Todos los aceleradores actuales son descendientes del Ciclotrón de Lawrence de los años 30 en Berkeley para romper átomos lanzando protones contra núcleos.
- El Bevatrón de Berkeley creó antiprotones.
En el Supercolisionador Superconductor se hubieran podido descubrir las compañeras supersimétricas de las partículas conocidas, descubrir que los quarks no son partículas elementales, nuevas fuerzas consecuencia de nuevas simetrías internas u obtenido más información acerca de la materia oscura, uno de los grandes enigmas de la física actual.
La materia visible se insuficiente para explicar el movimiento de las estrellas periféricas de las galaxias y requeriría de un nuevo tipo de materia para ser explicado
La materia oscura no puede ser materia ordinaria porque entonces las predicciones del modelo del Big Bang de producción de estas partículas en los primeros minutos de la expansión del universo no estarían de acuerdo con la observación tal y como lo están.
Si en los aceleradores encontráramos nuevas partículas estables y pudiéramos medir sus propiedades, entonces podríamos calcular su ritmo de producción en el universo primitivo y decidir si constituye toda la materia oscura que falta para explicar el ritmo actual de expansión del universo.
El satélite COBE ha estudiado irregularidades del fondo cósmico de microondas de cuando el universo tenía 300.000 años. En ese momento se hizo transparente a la radiación (de fotones) al ser los electrones capturados por los núcleos formando átomos neutros. Estas irregularidades no se podían deber a galaxias jóvenes en formación pues eran iirregularidades muy grandes de zonas que ya habían comenzado el colapso gravitatorio. Esta materia no podía ser la ordinaria porque las inhomogeneidades de esta materia no podía haber experimentado ningún crecimiento significativo hasta que el universo se hubiera hecho transparente a la radiación. La presión existente de la propia radiación hubiera dispersado cualquier acumulación de materia.
Sin embargo la materia oscura exótica que está compuesta de partículas eléctricamente neutras se habría hecho transparente a la radiación mucho antes, y así hubiera comenzado su condensación gravitatoria mucho más cerca del principio, produciendo inhomogeneidades a escalas galácticas mucho mayores, quizás suficientes para haber crecido hasta las galaxias actuales.
Además estos grandes experimentos de tecnología punta como los aceleradores son como una especie de locomotora industrial que obligua a avances en diversas tecnologías cruciales: criogenia, diseño de bobinas, computación en tiempo real. Es también un recurso intelectual para retener el talento.
Nadie sabe si un acelerador nos permitirá dar un último paso hacia la teoría final. Para el autor estas máquinas son los continuadores necesarios de una progresión histórica de los grandes instrumentos científicos, que se remontan mucho tiempo antes de los aceleradores actuales de Brookhaven, el CERN, DESY, Fermilab, KEK y SLAC hasta el ciclotrón de Lawrence y el tubo de rayos catódicos de Thomson y, mucho más atrás, hasta el espectroscopio de Frauenhofer y el telescopio de Galileo. Se descubran o no las leyes de la naturaleza, supone algo grande para nosotros continuar la tradición de someter la naturaleza a examen, de preguntar una y otra vez por qué es como es.
CMS, Solenoide Compacto de Muones, es uno de los experimentos del Gran Colisionador de Hadrones en el CERN, en la actualidad el acelerador más potente del mundo
Sin embargo el proyecto del SSC fue cancelado el 1993 por motivos políticos.
Opinión Personal
En este libro se plantea la razonable hipótesis de que exista una teoría final y fundamental porque la historia nos muestra que nuestras teorías cada vez son más fundamentales y se apoyan en cada vez menos principios básicos. Gracias también a nuestra experiencia con las teorías actuales más exitosas, este teoría final debería apoyarse en principios de simetría que le dieran una rigidez e inevitabilidad lógica, además de simplicidad. Simplicidad, inevitabilidad lógica y consistencia interna es lo que dan belleza a las teorías. Y se espera que la teoría final sea bella. Una posible candidata a teoría final es la teoría de supercuerdas, aunque actualmente está atravesando un período de dificultades.
En los primeros capítulos se repasa la mecánica cuántica y tres de las teorías más existosas y bellas de la física: la relatividad general, la electrodinámica cuántica y la teoría electrodébil. Las tres están basadas en principios de simetría y han sido y son confirmadas por los experimentos hasta un gran nivel de precisión. La mecánica cuántica es también una teoría en excelente acuerdo con la observación, pero existe un cierto descontento y desconcierto por el hecho de que solo permita calcular probabilidades y sobre lo que ocurre en el momento de la medición. La interpretación de Copenhague es operativa pero no acaba de resultar satisfactoria.
Lo que más me ha gustado de este libro es descubrir hasta que punto las teorías actuales de la física están basadas en principios de simetría que implican la aparición de ciertas interacciones o fuerzas. Estos principios de simetría proporcionan una inevitabilidad y simplicidad a las teorías que las hace bellas.
En este sentido, se espera que la teoría final posea un gran número de simetrías que determinen las interacciones y que le aporten una rigidez lógica, inevitabilidad y simplicidad que la hagan bella y elegante. De la física actual, se considera que únicamente la mecánica cuántica será incorporada por la teoría final prácticamente sin modificaciones, pues no se ha conseguido modificarla minimamente sin llegar a absurdos lógicos o sin dejar de realizar predicciones acertadas.

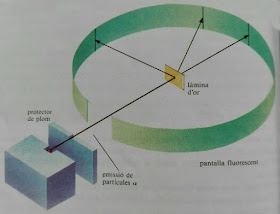
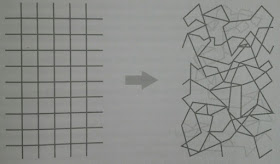
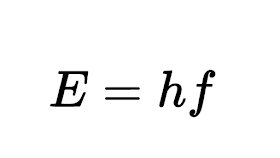


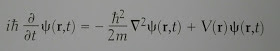



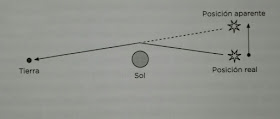
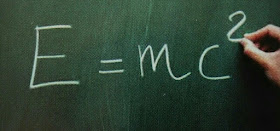
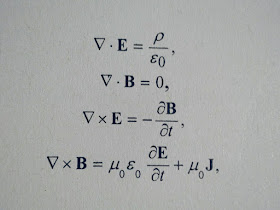
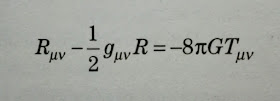
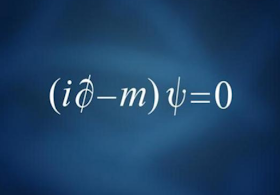
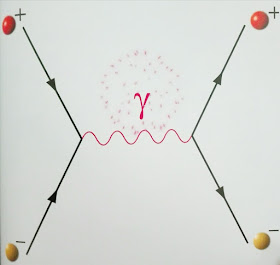

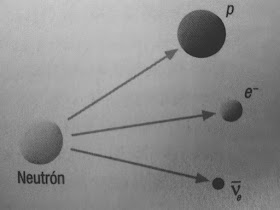
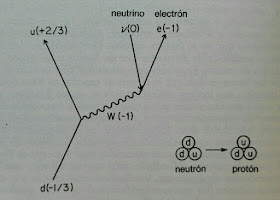
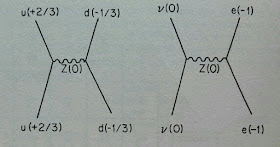
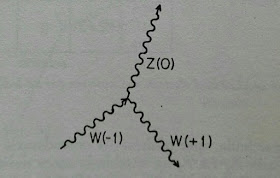
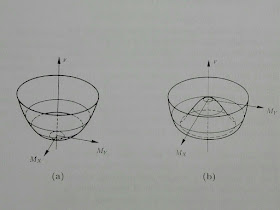
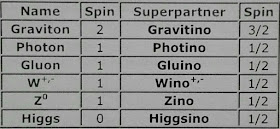

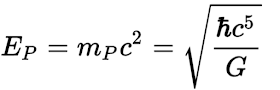
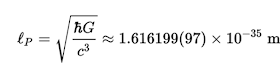

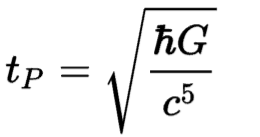
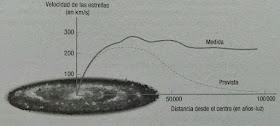

<>.Teoría Universal de la Compensación de Fuerzas <>
ResponderEliminarEnviado desde mi móvil Huawei y 7.
Nota:Respuesta Fuerzas, contrarios., necesnec ayuda [ €] + entregan correo electrónico . Veo, confiando Ustedes wwwtlpenergi@hotmail.com wwwtlpenergi@hotmail.com. wwwTLPenergi.m.isabel@hotmail.com ¡OJO! Mayuscula...M.Isabel@hotmail.com España. ( Madrid ) Tenemos la respuestasr.. <>
<> Teoría Universal de la Compensación de Fuerzas. <> Ambrosio@Isabel.com
ResponderEliminarEsperando respuestas, Fuerza Nuclear debil gravedad, Mas, etce