Esta entrada se un resumen y mi opinión personal del libro Los Primeros Tres Minutos del Universo, escrito por Steven Weinberg. Lo leí por primera vez en mi época universitaria y recuerdo que me encanto por la sencillez con la que el autor explica conceptos algo complicados.
Índice
Prefacio
1. Introducción: el gigante y la vaca
2. La expansión del universo
3. El fondo de radiación cósmica de microondas
4. Receta para un universo caliente
5. Los tres primeros minutos
6. Una disgresión histórica
7. La primera centésima de segundo
8. Epílogo: la perspectiva futura
Prefacio
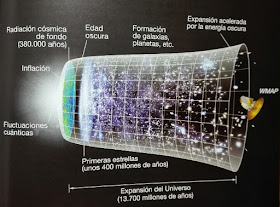
Este libro escrito por Steven Weinberg trata del universo primitivo, y en particular del nuevo conocimiento del universo primitivo que ha originado el descubrimiento del fondo cósmico de microondas en 1965. En el universo primitivo, especialmente en la primera centésima de segundo, los problemas de las partículas elementales se unen a los problemas de la cosmología.
Fondo Cósmico de Microondas predicho correctamente por el modelo del Big Bang.
La homogeneidad del Fondo Cósmico de Microondas se explica por un brote intenso de gravedad repulsiva como la energía oscura llamada inflación instantes posteriores al Big Bang
Este libro no se centra en la estructura a gran escala del universo ni en los modelos basados en la relatividad general de Einstein, de Sitter, Lemaître o Friedmann.
1. Introducción
Un resumen de la historia del universo primitivo según el modelo estándar de la cosmología sería el siguiente. En el comienzo hubo una explosión no convencional que tuvo lugar en todos los puntos del espacio de un universo que podría considerarse infinito o finito pero sin frontera (como la superficie de una esfera).
Expansión del universo tras el Big Bang
Al cabo de una centésima de segundo aproximadamente, que es el momento más primitivo del que podemos hablar con cierta seguridad, la temperatura del universo fue de unos cien mil millones de grados centígrados. A dicha temperatura no pueden mantenerse unidos los componentes de la materia ordinaria: moléculas, átomos e incluso núcleos atómicos. Lo único que existía eran partículas elementales, principalmente electrones, positrones, neutrinos y fotones en forma de radiación. Aunque actualmente los positrones apenas existen (apenas se encuentran en los rayos cósmicos o la radiactividad) en el universo primitivo existían en número parecido al de los electrones.
Estas partículas existentes en un número parecido eran creadas continuamente a partir de la energía pura y aniquiladas de nuevo tras una corta vida. Su número no estaba prefijado y dependía del balance entre los procesos de creación y destrucción. De este balance podemos inferir que la densidad de esta sopa cósmica a una temperatura de cien mil millones de grados era unos cuatro millones de veces mayor que la del agua.
Hubo también una pequeña contaminación de protones y neutrones por cada mil millones de electrones o fotones. Este número es la cantidad crucial que tuvo que derivarse de las observaciones para elaborar el modelo estándar del universo. El fondo cósmico de microondas fue una medición de esa magnitud.
A medida que la explosión continuó, la temperatura fue disminuyendo hasta alcanzar los treinta mil millones de grados centígrados después de una décima de segundo, diez mil millones de grados después de un segundo y tres millones de grados después de unos catorce segundos. Esta temperatura era lo suficientemente baja como para que los electrones y los positrones comenzaran a aniquilarse más rápidamente de lo que podían ser recreados a partir de los fotones y los neutrinos. La energía liberada en este aniquilamiento de materia hizo disminuir temporalmente la velocidad a la que se enfriaba el universo, pero la temperatura continuó cayendo hasta alcanzar los mil millones de grados al final de los tres primeros minutos. Esta temperatura fue entonces suficiente para que los protones y los neutrones comenzaran a crear núcleos complejos, comenzando por el deuterio, que a su vez crearon núcleos de helio, más estables, gracias a que la densidad aún era elevada (algo menor que la del agua).
Según el Modelo del Big Bang, los primeros átomos de Hidrógeno y Helio se crearon mediante reacciones de fusión nuclear gracias a las elevadas temperaturas
Al final de los tres primeros minutos, el universo contenía principalmente luz, neutrinos y antineutrinos. Había también una pequeña cantidad de material nuclear, formado por un 73% de hidrógeno y un 27% de helio y por un número igualmente pequeño de los electrones que habían quedado de la época de los aniquilamientos entre electrones y positrones.
Tras algunos cientos de miles de años el universo se había enfriado lo suficiente para que los núcleos capturaran electrones y formaran átomos de hidrógeno y helio.
Debido a la gravitación el gas resultante comenzó a formar agrupamientos que finalmente se condensarían para formar galaxias y las estrellas del universo actual. Pero los ingredientes con los que empezarían su vida las estrellas serían exactamente los preparados durante los primeros tres minutos.
Este modelo estándar tiene dos inconvenientes:
- No es preciso hasta la primera centésima de segundo. No es capaz de realizar predicciones para un tiempo anterior.
- Necesita el establecimiento de condiciones iniciales, como la proporción inicial de mil millones a uno entre los fotones y las partículas nucleares. Preferiríamos una mayor inevitabilidad lógica en la teoría.
2. La expansión del universo
A pesar de que las estrellas parecen inmóviles en el firmamento, se alejan de nosotros a gran velocidad. Nuestro conocimiento sobre la expansión del Universo se apoya en el efecto Doppler que provoca un desplazamiento de los espectros de absorción de las estrellas cuando la luz pasa de su superficie caliente a su atmósfera externa, más fría. Cada línea es causada por la absorción de luz por un elemento químico específico, lo que permitió afirmar que los elementos que forman las estrellas son los mismos que encontramos en la Tierra.
La medición de velocidades por la observación de corrimientos Doppler es una técnica intrínsecamente exacta porque las longitudes de onda de las líneas espectrales pueden medirse con gran precisión. Asimismo, la técnica conserva su exactitud cualquiera que sea la distancia de la fuente luminosa siempre que haya bastante luz para recoger líneas espectrales contra la radiación del cielo nocturno.
El efecto Doppler no empezó a dar resultados de importancia cosmológica hasta que comenzó a aplicarse a objetos muy lejanos, mucho más que las estrellas visibles. En el cielo nocturno, además de la Luna y los planetas hay otros dos objetos visibles de mayor importancia cosmológica: la Vía Láctea y la nebulosa de Andrómeda. Los astrónomos del siglo XVII y XVIII detectaron estas nebulosas como objetos que les impedían detectar los cometas. Por eso Charles Messier publicó en 1781 el catálogo Nebulosas y Cúmulos Estelares con las 103 nebulosas detectadas hasta entonces. Eran zonas a evitar en la observación de cometas. En este catálogo la nebulosa de Andrómeda era la M31.
No fue hasta 1923 con el nuevo telescopio de 2,5 metros del Monte Wilson que Edwin Hubble descubrió que las nebulosas eran realmente agrupaciones de estrellas o galaxias. Con este telescopio Hubble halló que sus brazos espirales contienen unas pocas estrellas variables brillantes, con el mismo tipo de variación periódica en la luminosidad que ya se conocía en una clase de estrellas de nuestra galaxia llamadas variables cefeideas. Esto es importante porque existe una estrecha relación entre los periodos observados de variación en las cefeideas y sus luminosidades absolutas.
La luminosidad absoluta es la energía radiante total emitida por un objeto astronómico en todas las direcciones. La luminosidad aparente es la energía radiante que recibimos en cada centímetro cuadrado del espejo de nuestro telescopio. Esta depende de la luminosidad absoluta y de la distancia. Por tanto conociendo ambas luminosidades puede obtenerse la distancia. Así pudo Hubble calcular la distancia a la galaxia de Andrómeda.
Entre 1910 y 1920 Vesto Melvin Sipher descubrió que las líneas espectrales de muchas nebulosas están ligeramente corridas hacia el rojo o el azul. Prácticamente todas hacia el rojo (salvo algunas vecinas como Andrómeda). Estos corrimientos fueron rápidamente interpretados como causados por un efecto Doppler, con lo que todas las galaxias se estaban alejando unas de otras.
En 1929 Edwin Hubble confirmó esta interpretación con el descubrimiento de que los corrimientos hacia el rojo aumentaba aproximadamente en proporción a su distancia de nosotros.
Esto es lo que cabe esperar si se asume la hipótesis de que el universo tiene el mismo aspecto para cualquier observador y cualquiera que sea la dirección en la que mire. A esta hipótesis tan natural se le llama el principio cosmológico. Además, si el universo es isótropo a nuestro alrededor, también debe serlo en cualquier punto del universo. Por ello si el universo es isótropo a nuestro alrededor, también es necesariamente homogéneo. La ley de Hubble es una consecuencia matemática directa de este principio y, mediante la medición de corrimientos Doppler, permite estimar la distancia de objetos muy remotos a partir de sus velocidades.
El principio cosmológico solo es válido a escalas a partir de 100 años-luz, la distancia entre cúmulos de galaxias, ni tampoco lo sería para velocidades cercanas a la de la luz debido a los efectos de la relatividad especial. Es decir, para estas velocidades es posible que la ley de Hubble no sea del todo correcta.
La equivalencia entre masa y energía de la relatividad especial es una de las principales consecuencias de la relatividad especial
En 1931 la constante de Hubble tenía un valor de 170 kilómetros por segundo por cada millón de años luz de distancia. Así por ejemplo, una velocidad de 20000 kilómetros por segundo supone una distancia de 120 años-luz. Es constante para todas las galaxias en un momento dado pero varía con el tiempo a medida que el universo evoluciona.
Tras más de medio siglo de observaciones la modificación más importante de las conclusiones de Hubble es una revisión de la escala de distancias extragalácticas en parte por una reevaluación de la relación entre el periodo y la luminosidad de las Cefeidas, con lo que las distancias se estiman 10 veces mayores, con lo que la constante de Hubble pasa a ser de solo 15 kilómetros por segundo por cada millón de años luz de distancia.
Si las galaxias se están alejando unas de otras, entonces deben haber estado más cerca en el pasado. Con una velocidad proporcional a la distancia, en el pasado deben haber estado unidas en el mismo tiempo. El inverso de la constante de Hubble nos daría el tiempo de expansión característico. Sin embargo la edad verdadera del universo es menor porque la velocidad de expansión de las galaxias se ha reducido por influencia de su mutua gravitación.
En un intervalo de tiempo suficientemente pequeño para que la constante de Hubble se mantenga constante, el incremento de separación entre dos galaxias típicas será el producto de su velocidad relativa por el tiempo transcurrido, o bien, por el producto de la constante de Hubble, la separación y el tiempo. Así, la razón del incremento de la separación a la separación misma estará dada por el producto de la constante de Hubble por el tiempo transcurrido, que es igual para todo par de galaxias.
Hasta ahora, en el marco de un universo en expansión, la luz ha desempeñado el papel de un mero mensajero estelar que transmite información sobre la distancia y la velocidad de las galaxias. Sin embargo el universo primitivo estaba dominado por la radiación y la materia ordinaria apenas desempeñaba el papel de una contaminación despreciable.
Un dato destacable es que la longitud de onda de todo rayo de luz aumenta en proporción a la separación entre galaxias a medida que el universo se expande. Por ejemplo si el corrimiento al rojo de un espectro es un 10%, entonces el universo es un 10% mayor que cuando la luz partió de esa fuente.
El análisis realizado hasta ahora sería sobre el aspecto cinemático del universo. El primero en tratar el aspecto dinámico fue Newton. Este dijo que el universo no podía ser finito porque entonces colapsaría hacia un punto por efecto de la gravedad. Si la materia estuviera dispersa uniformemente en un universo infinito no habría centro alguno sobre el que pudiera colapsar.
Con la llegada de la teoría de la relatividad general de Einstein en 1915 se facilitó la creación de modelos dinámicos del universo. En esta teoría utiliza la geometría curva no-euclidiana de Riemann para explicar la gravitación como un efecto de la curvatura del espacio-tiempo.
Ecuaciones de campo de la Relatividad General que proporcionan las gμν que caracterizan la geometría y la métrica el espacio-tiempo creado por una distribución de masa-energía concreta
Según la relatividad general la masa de una estrella como el Sol curva el espacio-tiempo tiempo haciendo que los planetas orbiten a su alrededor al seguir el camino más corto posible (geodésica) en un espacio-tiempo de cuatro dimensiones
En 1917 Einstein intentó aplicar su teoría para obtener una métrica del espacio-tiempo del universo bajo la hipótesis de que este fuera homogéneo, isótropo (principio cosmológico) y estático. Pero no pudo. Por ello añadió una constante cosmológica que contrarrestará el efecto atractivo de la gravedad.
Sin embargo este modelo no predecía el corrimiento hacia el rojo. Esto si que lo hacia el modelo de de Sitter, también de 1917, y por ello adquirió gran popularidad cuando estos se descubrieron. Esta solución parecía estática pero no lo era y el corrimiento al rojo era proporcional a la distancia porque esta solución satisface el modelo cosmológico, lo que implica una proporcionalidad entre la velocidad relativa y la distancia.
Sin embargo este modelo no predecía el corrimiento hacia el rojo. Esto si que lo hacia el modelo de de Sitter, también de 1917, y por ello adquirió gran popularidad cuando estos se descubrieron. Esta solución parecía estática pero no lo era y el corrimiento al rojo era proporcional a la distancia porque esta solución satisface el modelo cosmológico, lo que implica una proporcionalidad entre la velocidad relativa y la distancia.
En 1922 Alexander Friedmann encontró las soluciones general de la relatividad general para un universo homogéneo e isótropo. Fueron estos modelos de Friedmann, basados en las ecuaciones originales de Einstein, y no los modelos de Einstein y de Sitter, los que proporcionaron el fundamento matemático para la mayoría de las teorías cosmológicas modernas.
Ecuaciones de Friedmann obtenidas como solución de la Relatividad General
Los modelos de Friedmann pueden ser de dos tipos:
- Un universo espacialmente infinito si la densidad media de la materia es inferior a un umbral. En tal caso la expansión del universo seguirá eternamente.
- Un universo espacialmente finito pero ilimitado (sin frontera) si la densidad media de la materia es superior a un umbral. En tal caso la atracción gravitatoria revertiría la expansión.
La densidad crítica es proporcional al cuadrado de la constante de Hubble. Para H igual a 15 kilómetros por segundo y año-luz, la densidad crítica es de 5x10-30 gramos por centímetro cúbico o tres átomos de hidrógeno por metro cúbico.
En los modelos de Friedmann un universo estático es altamente inestable por el mismo motivo que una piedra lanzada al aire no queda suspendida en el aire.
Para calcular la velocidad de una galaxia respecto a nosotros no es necesaria la relatividad general. Solo hay que considerar el hecho de que en un escenario de simetría esférica, la masa del universo que importa es la comprendida en una esfera con nosotros en el centro y la galaxia que se aleja en su superficie (teorema de Birkhoff). Si ambas galaxias no estàn demasiado alejadas, el campo gravitatorio de la masa interior a la esfera será moderado, y podrá aplicarse la teoría newtoniana.
Con esta consideración podemos calcular la masa contenida en dicha esfera para calcular la velocidad de escape de la galaxia que se aleja. Esta velocidad resulta proporcional al radio de la esfera. Pero la ley de Hubble afirma que la velocidad real de una galaxia en la superficie de la esfera es proporcional a la distancia que nos separa de ella. Por tanto, el cociente de la velocidad real respecto a su velocidad de escape no depende del tamaño de la esfera, con lo que es la misma para todas las galaxias.
Según sean los valores de la constante de Hubble y la densidad cósmica, toda galaxia que se desplace según esta ley superará la velocidad de escape y escapará al infinito o caerá hacia nosotros en un momento futuro. La densidad crítica es el valor de la densidad cósmica a la que la velocidad de escape de cada galaxia es igual a la velocidad establecida por la ley de Hubble. La densidad crítica solo puede depender de la constante de Hubble, siendo realmente proporcional a su cuadrado.
Respecto a la dependencia temporal del tamaño del universo en su era primitiva, esta dependía como una potencia simple del tiempo, como una potencia de dos tercios si se podía despreciar la densidad de radiación, o como potencia de un medio si la radiación dominaba la materia.
El aspecto de los modelos de Friedmann no comprensibles sin la relatividad general es la relación entre la densidad y la geometría: abierto e infinito o cerrado y finito en función de la velocidad de escape o densidad de materia del universo.
Actualmente los datos observacionales no permiten concluir la geometría del universo pero parecen indicar que la velocidad de las galaxias es superior a la de escape, o la densidad de materia es inferior a la crítica, con lo que el universo se seguirá expandiendo eternamente.
Actualmente los datos observacionales no permiten concluir la geometría del universo pero parecen indicar que la velocidad de las galaxias es superior a la de escape, o la densidad de materia es inferior a la crítica, con lo que el universo se seguirá expandiendo eternamente.
Afortunadamente no es necesario un conocimiento de la geometría del universo a gran escala para extraer consecuencias sobre su comienzo gracias a que el universo tiene un horizonte que se contrae rápidamente a medida que nos remontamos hacia los comienzos. Este horizonte es aquella región del espacio desde la cual un rayo de luz ha podido alcanzarnos. El resto del Universo no tiene una influencia causal sobre nosotros. Cuando este tenía unos pocos minutos, el horizonte se hallaba solo a unos pocos minutos-luz. Al remontarnos hacia el inicio, la distancia del horizonte se contrae más rápidamente (proporcional al tiempo) que el tamaño del universo (potencia un medio o dos tercios del tiempo. Para tiempos cada vez más remotos, el horizonte encierra partes cada vez menores del universo.
3. El fondo de radiación cósmica de microondas
En 1964 los radioastrónomos Arno Penzias y Robert Wilson comenzaron a usar una antena de bajo ruido en forma de cuerno con un reflector de 20 pies para medir la intensidad de ondas de radio en la banda de las microondas emitidas por nuestra galaxia fuera del plano de la Vía Láctea.
Antena en forma de cuerno o bocina con la que Penzias y Wilson descubrieron la radiación del Fondo Cósmico de Microondas
Esta medida es dificultosa porque las ondas de radio de nuestra galaxia son como un tipo de ruido similar al ruido eléctrico que producen los movimientos al azar de los electrones dentro de la estructura de la antena de radio y los circuitos del amplificador o, también, al ruido que recoge la antena de la atmósfera terrestre (este depende de su espesor y, por tanto, de si la antena se apunta al cenit o al horizonte). Otra dificultad añadida es que al no estudiar una fuente puntual, el ruido de la antena no puede compararse y compensarse con el de una zona ajena a la fuente.
Las pruebas anteriores de este sistema, en efecto, habían revelado algo más de ruido del esperado independiente de la dirección, del momento del día y de la estación del año. El hecho de que no vinieran de una dirección concreta hacía pensar que esa señal de microondas no procedia de la Vía Láctea sino de un volumen mayor del universo.
Cualquier cuerpo a una temperatura superior al cero absoluto emite siempre un ruido radioeléctrico producido por los movimientos térmicos de sus electrones. Dentro de un cuerpo opaco, la intensidad de ruido en cualquier longitud de onda solo depende de la temperatura, con lo que se puede describir su intensidad a una longitud de onda determinada en términos de una temperatura equivalente. Esta sería la de las paredes de un cuerpo dentro de la que el ruido tendría la intensidad observada.
Penzias y Wilson hallaron una temperatura equivalente de ruido de entre 2,5 y 4,5 grados Kelvin. Se trataba del avance cosmológico más importante desde el descubrimiento de los corrimientos hacia el rojo.
En 1965 P. J. E. Peebles, inspirado por las ideas del físico experimental Robert Dicke, afirmó que debía existir un intenso fondo de radiación en el universo primitivo durante los primeros minutos del universo para frenar las reacciones nucleares que hubieran transformado todo el hidrógeno en elementos más pesados, en contradicción con el hecho de que el universo actual esta formado por hidrógeno en sus tres cuartas partes.
La temperatura equivalente de esta radiación ha disminuido debido a la expansión del Universo en proporción inversa al tamaño de este debido al corrimiento al rojo. Por ello el universo actual debe estar lleno de radiación, pero de una temperatura mucho menor. Los cálculos teóricos para que el fondo cósmico de microondas haya mantenido la producción de helio y elementos más pesados en los primeros minutos dentro de los límites conocidos, tuvo que ser tan intensa que su temperatura actual sería al menos de 10K.
Podemos preguntarnos si este fondo de radiación es realmente un remanente del universo primitivo y si sus propiedades concuerdan con las predicciones teóricas. Para responder debemos considerar la concepción cuántica de la radiación electromagnética según la cual esta consiste en partículas llamadas fotones. Los fotones no tienen masa y carga nula pero un momento, energía y espín bien definidos.
La energía solo puede radiarse de manera discreta o discontinua en paquetes o cuantos cuya energía es proporcional a la frecuencia
En los últimos 10.000 millones de años el universo es bastante transparente con lo que la luz nos llega bastante bien porque los fotones apenas son absorbidos o dispersados. Pero en los primeros 700.000 años el universo era mucho más caliente y denso y se ha enfriado debido a la expansión. Tanto que los átomos eran desmenuzados por la radiación. Los fotones eran pues dispersados constantemente por los electrones libres. Cualesquiera que fuesen las condiciones iniciales del universo, esta interacción constante debía llegar a un estado de equilibrio estadístico o térmico, en el que las condiciones del sistema serán aquellas que lo mantengan.
En equilibrio la temperatura está definida y es uniforme en todo el sistema. Es cierto que el equilibrio térmico no puede ser perfecto porque, al fin y al cabo, el universo se está expandiendo. Pero podemos considerarlo así tendiendo en cuenta que las partículas se movían e interaccionaban a una velocidad mucho mayor que la de dicha expansión.
En equilibrio la temperatura está definida y es uniforme en todo el sistema. Es cierto que el equilibrio térmico no puede ser perfecto porque, al fin y al cabo, el universo se está expandiendo. Pero podemos considerarlo así tendiendo en cuenta que las partículas se movían e interaccionaban a una velocidad mucho mayor que la de dicha expansión.
En equilibrio termico, la mecánica estadística nos dice que el estado o propiedades térmicas del sistema únicamente dependerá de la temperatura y las densidades de unas pocas magnitudes conservadas.
Para discernir las propiedades esperables del fondo cósmico de microondas debemos saber cuáles son las propiedades de la radiación en equilibrio térmico con la materia. Esta fue precisamente la cuestión que dio origen a la mecánica cuántica y a la interpretacion de la radiación en términos de fotones. Las propiedades de esta en estado de equilibrio térmico con la materia solo dependen de la temperatura. Más específicamente, la densidad de energía de tal radiación está dada por la distribución de Planck, que depende solo de la longitud de onda y la temperatura (es independiente de la naturaleza de la materia). Es la misma fórmula que para el caso del cuerpo negro, con lo que se puede interpretar la intensidad de ruido de radio en función de una temperatura equivalente.
La hipótesis de cuantización de la energía que lleva a la distribución de Planck y con la que Einstein explicó el efecto fotoeléctrico nos dice que la energía de todo fotón es inversamente proporcional a la longitud de onda. A cualquier temperatura dada, la radiación de cuerpo negro contendrá muy pocos fotones de energía elevada o longitudes de onda cortas. Un fotón con longitud de onda de luz visible tiene una energía de unos 2,5 eV, lo que permite a esos fotones provocar reacciones químicas esenciales para la vida, como la fotosíntesis. En cualquier caso, la energía de un fotón es muy pequeña en términos macroscópicos, por lo que parece que los fotones se mezclan en una corriente continua de radiación.
Considerando que la mecánica estadística nos dice que la energía del fotón típico es proporcional a la temperatura y que la fórmula de Einstein muestra que la longitud de onda es inversamente proporcional a la energía, entonces la longitud de onda típica de los fotones en la radiación del cuerpo negro es inversamente proporcional a la temperatura. Por ejemplo, a la temperatura de 1K, la energía de radiación de un cuerpo negro se concentra alrededor de 0,29 centímetros, y es proporcionalmente menor a temperaturas mayores. A temperatura de 300K, la longitud de onda será de 0,29 centímetros dividido entre 300, es decir una milésima de centímetro, en la banda del infrarrojo. En cambio, la superficie del Sol está a 5800K, cuya longitud de onda asociada cae en el medio de la banda visible.
Además la distancia entre dos fotones en la radiación de cuerpo negro es aproximadamente igual a la longitud de onda del fotón típico. Como la longitud de onda es inversamente proporcional a la temperatura, en la radiación de cuerpo negro el número de fotones en un volumen dado es proporcional al cubo de la temperatura.
Si la temperatura aumenta en un factor f, solo hay que reducir la longitud de onda en un factor f y aumentar la densidad de energía en un factor f3.
Por tanto si la densidad de energía es proporcional a la densidad de fotones por la energía media de cada fotón, entonces equivaldrá a kT3 multiplicado por la temperatura y una constante de proporcionalidad, es decir, será proporcional a la cuarta potencia de la temperatura.
Esta es la llamada ley de Stefan-Boltzmann. Si en el pasado la temperatura fue 1000 veces mayor, la densidad de energía lo fue un billón de veces.
Cuando el universo se enfrió entorno a los 3000K, los núcleos y los electrones se combinaron en átomos (recombinación) haciendo el universo transparente a la radiación y permitiendo que esta se expandiera libremente. En ese momento la distribución de energía por longitud de onda venía dada por la fórmula de Planck para el cuerpo negro para una temperatura de 3000K. Desde entonces los fotones no se han creado ni destruido, sino que la distancia media entre fotones aumentó en proporción al tamaño del universo. Como el efecto del corrimiento al rojo es estirar la longitud de onda del fotón, esta aumentó en proporción al tamaño del universo. Se puede demostrar que la radiación que llena el universo seguiría viniendo descrita exactamente por la fórmula de Planck para el cuerpo negro a medida que este se expandiese, aunque ya no estuviera en equilibrio térmico con la materia. Este es el único efecto de la expansión del Universo.
Todas las medidas realizadas desde el descubrimiento de la intensidad del fondo cósmico de microondas confirman que es compatible con una distribución de Planck de la energía en función de la longitud de onda con una temperatura entre 2,7 y 3K. Hasta este punto las mediciones se habían realizado para longitudes de onda mayores que la del pico, que sería de 0,29 ccentímetros dividido entre los 3K de la temperatura del fondo cósmico de microondas, es decir, de unos 0,1 centímetros. Esta zona es conocida como zona de Rayleigh-Jeans, y es la compatible con la mecánica clásica. Pero estas longitudes de onda pertenecen al infrarrojo, banda absorbida por la atmósfera terrestre. Para ello es necesario realizar mediciones más allá de la atmósfera.
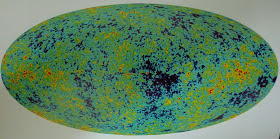
Los satélites COBE, WMAP y PLANCK las han realizado confirmando que se trata efectivamente de una radiación compatible con la distribución de Planck de energía en función de la longitud de onda. Además con estos satélites se han detectado pequeñas anisotropías direccionales que no se hubieran podido detectar desde la superficie de la Tierra debido a que la atmósfera no es realmente isótropa como se supone en estas mediciones. De hecho no se espera que esta radiación sea perfectamente isótropa. Dos motivos serían:
Los satélites COBE, WMAP y PLANCK las han realizado confirmando que se trata efectivamente de una radiación compatible con la distribución de Planck de energía en función de la longitud de onda. Además con estos satélites se han detectado pequeñas anisotropías direccionales que no se hubieran podido detectar desde la superficie de la Tierra debido a que la atmósfera no es realmente isótropa como se supone en estas mediciones. De hecho no se espera que esta radiación sea perfectamente isótropa. Dos motivos serían:
- Pequeñas zonas de temperatura ligeramente superior a la media correspondientes a galaxias en las primeras etapas de formación con una posible extensión mayor que medio minuto de arco.
- Variación continua por el movimiento de la Tierra respecto al fondo cósmico de microondas de unos 300 kilómetros por segundo. Por efecto Doppler debe haber una variación del 0,1 por ciento, con lo que la temperatura de radiación debe variar en un ±0,1%.
La existencia del fondo cósmico de microondas nos proporciona indicios de que la radiación y la materia estuvieron alguna vez en equilibrio térmico. ¿Qué nos dice el valor de su temperatura de 3K?
A una temperatura dada el número de fotones por unidad de volumen es proporcional al cubo de la temperatura. Para una temperatura de 3K, el fondo de radiación contiene 550.000 fotones por litro. Sin embargo, la densidad de las partículas nucleares en el universo actual está entre 6 y 0,03 partículas por metro cúbico. Así en función del valor real de la densidad de partículas hay entre 100 y 20000 millones de fotones por nucleón en el universo actual. Esta proporción ha permanecido aproximadamente constante durante largo tiempo porque desde que el universo se hizo transparente (recombinacion), los fotones y nucleones no han sido creados ni destruidos. Esta es la conclusión cuantitativa más importante que debe extraerse del fondo cósmico de microondas. Por claridad podemos suponer que ha habido 1000 millones de fotones por nucleón de media en el universo.
Esto implica que en el universo primitivo a temperaturas superiores a 3000K la presión de radiación era tan grande que impedía que la materia se fuera apelmazando en grumos que finalmente crearan galaxias. Por eso en esta etapa del universo no habia estrellas ni galaxias, solo una sopa ionizada e indiferenciada de materia y radiación.
Esta enorme proporción entre fotones por nucleón nos hace pensar que en sus inicios el universo estaba dominado por la radiación, siendo la energía de esta (energía por fotón por el número de fotones) mayor que la contenida en la materia según E=mc2. A 3K la energía media de un fotón en la radiación de cuerpo negro de 3K es de 0,0007eV mientras que la de un nucleón es de 939eV. Con 1000 millones de fotones por nucleón la energía de la materia es la dominante (más fotones y más energéticos que en la actualidad).
Pero en tiempos anteriores la temperatura era mayor, mientras que la energía contenida en un nucleón era la misma. Para una energía de un fotón superior a 1eV, la radiación domina a la materia. Esto ocurrió cuando la temperatura era 1300 veces mayor que en la actualidad, es decir, de unos 4000K. Este punto marca la transición entre una era dominada por la radiación y la era actual dominada por la materia, en la que la mayor parte de energía está en la masa de las partículas nucleares. Es sorprendente que esta transición ocurriera en la misma época en que el universo se volvió transparente a la radiación. No hay una explicación.
Pero en tiempos anteriores la temperatura era mayor, mientras que la energía contenida en un nucleón era la misma. Para una energía de un fotón superior a 1eV, la radiación domina a la materia. Esto ocurrió cuando la temperatura era 1300 veces mayor que en la actualidad, es decir, de unos 4000K. Este punto marca la transición entre una era dominada por la radiación y la era actual dominada por la materia, en la que la mayor parte de energía está en la masa de las partículas nucleares. Es sorprendente que esta transición ocurriera en la misma época en que el universo se volvió transparente a la radiación. No hay una explicación.
Lo importante es que antes de que el universo se volviera transparente, el universo podía considerarse como compuesto principalmente de radiación, con solo una pequeña contaminación de materia. La enorme densidad del universo disminuyó debido a su expansión (corrimiento al rojo) permitiendo que la contaminación de partículas nucleares y electrones formaran las estrellas, rocas y seres vivos del universo actual.
4. Receta para un universo caliente
En este capítulo se examina la época en que la radiación dominó a la materia, a partir de los tres primeros minutos del universo y hasta unos pocos de cientos de miles de años en que la materia se hizo nuevamente más importante que la radiación.
Para ello debemos saber cómo se relaciona la temperatura con el tamaño del universo a medida que este se expande. En el caso de expansión libre (universo transparente a la radiación), vimos que la temperatura habría disminuido en proporción inversa al tamaño del universo. Esto también es válido cuando la radiación no se expande libremente porque la enorme cantidad de fotones por partícula implicaban tal cantidad de colisiones que estas forzaban a la temperatura de la materia a adecuarse a la de la radiación.
Sin embargo si remontamos el tiempo suficiente, la temperatura era tan elevada que las colisiones entre fotones podían crear pares virtuales si la energía era al menos E=mc2. Estas partículas fueron importantes en la regulación de ciertos procesos nucleares como el ritmo de la expansión del universo.
Para estimar esta creación de pares necesitamos saber la energía de cada fotón en función de la temperatura. Esta energía puede aproximarse por KT, siendo K la constante de Boltzmann cuyo valor es 0,00008617eV por Kelvin. A temperatura de 3000K, la energía característica de cada fotón era de aproximadamente 0,26eV, del orden de magnitud necesario para impedir que los electrones sean capturados por los núcleos.
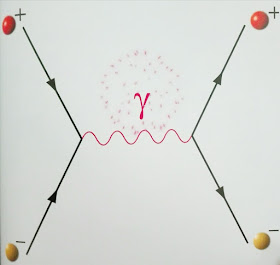
Diagrama de Feynman en que un electrón y un positrón se aniquilan en fotones que a su vez se desintegra en un par electrón-positrón
Las partículas de materia más ligeras que pueden crearse a partir de la colisión entre fotones son el electrón y su antipartícula el positrón cuya masa es de 0,511 millones de eV. Si dividimos este valor entre la constante de Boltzmann 0,00008617, obtenemos una temperatura de 6000 millones de grados, muy superior al del centro del Sol (unos 15 millones de grados). Por ello no estamos acostumbrados a ver surgir electrones y positrones de la luz brillante. La siguiente partícula más ligera es el muón, con una masa aproximada de 105 millones de eV. Para producir un par muón-antimuón la temperatura debía ser de 1,2 billones de grados.
En las condiciones de elevada temperatura y densidad que prevalecieron en el universo primitivo, el número de partículas dependía de la condición básica de equilibrio térmico, que exige que el numero de cada tipo de partículas cuyo umbral de temperatura esté por debajo de la temperatura real sea aproximadamente igual al número de fotones.
Pero a temperaturas superiores al umbral, la masa de una partícula material puede ser despreciada respecto a su energía cinética KT, de modo que se comportará de modo muy similar a un fotón.
En estas condiciones la densidad de energía y presión aportada por cada tipo de partícula material son proporcionales a la cuarta potencia de la temperatura, como en el caso de los fotones. Así la densidad de energía del universo es proporcional a la cuarta potencia de la temperatura por el número de especies de partículas creables como par virtual.
Las antipartículas deben ser consideradas como una especie distinta, así como cada uno de los dos estados de espín del electrón y del fotón. Finalmente los fermiones como el electrón obedecen el principio de exclusión de Pauli que disminuye su contribución a la densidad de energía total en un factor de siete octavos. Por tanto la densidad de energía del universo es proporcional a la cuarta potencia de la temperatura por el número efectivo de especies de partículas creables como par virtual.
Pero,¿Cuándo el universo estuvo a tan altas temperaturas? Puede demostrarse que el tiempo que tarda el universo en enfriarse de una temperatura a otra es proporcional a la diferencia de los inversos de los cuadrados de esas temperaturas. Si la temperatura se reduce por 10, el tiempo aumenta por 100. El tiempo que necesitó el universo para enfriarse de 100 millones de grados a 3000K fue de 700.000 años.
Tan pronto como admitimos la posibilidad de un exceso de materia sobre la antimateria en los tres primeros minutos, se nos presenta el problema de confeccionar una lista detallada de ingredientes para el universo primitivo. Para ello debemos considerar el hecho de que en un sistema en equilibrio térmico, todas sus propiedades quedan univocamente determinadas una vez específicados los valores de las magnitudes conservadas. Se considera que hay tres magnitudes conservadas para cualquier temperatura posible, cuyas densidades deben ser especificadas en nuestra receta para el universo primitivo:
1) La carga eléctrica. Su conservación es la base, por ejemplo, de la teoría electromagnética de Maxwell.
2) El número bariónico. Este número no parece tener ningún significado dinámico como la carga. No es fuente de ningun campo como el gravitatorio o el electromagnético.
3) El número leptónico. Los leptones son el electrón, el muon el tau, sus neutrinos asociados y las antipartículas de todos ellos.
Igual que el número de fotones, la carga, el número bariónico y el número leptónico por unidad de volumen varían sencillamente en proporción inversa al cubo del tamaño del universo. Por tanto la carga, el número bariónico y el número leptónico por fotón permanecen fijos, con lo que podemos formular nuestra receta especificando los valores de las magnitudes conservadas como una proporción con respecto al número de fotones.
Actualmente la carga neta en el universo es nula, con lo que también lo fue en el pasado. Respecto al numero bariónico, los únicos bariones estables son el protón y el neutrón y no hay antimateria en el universo actual. Sabemos que en el fondo cósmico de microondas la proporción era de un nucleón por cada 1000 millones de fotones. Por tanto, el número bariónico respecto al número de fotones es de 10-9.
En el pasado, cuando la temperatura era en torno al umbral de los protones y neutrones, 1013K, el numero de nucleones sería similar al de fotones, lo que significa que la proporción materia antimateria de los bariones era de 1 entre mil millones, lo que no deja de ser extraño.
Respecto al numero leptónico, si la carga neta del universo es nula, es que hay tantos electrones como protones, que son el 87% de los bariones. Pero los neutrinos y antineutrinos tienen número leptionico de 1 y -1 respectivamente. Sin embargo como estos apenas interaccionan (solo mediante la gravedad y la fuerza nuclear débil), puede que haya gran cantidad de neutrinos y antineutrinos a nuestro alrededor sin que sospechemos de su presencia. Al apenas interactuar es muy difícil recoger información experimental sobre ellos tanto de ahora como del universo primitivo. Se podrían buscar umbrales pero serían tan vagos que apenas aportarian información. Al final se considera que el número leptónico es muy inferior al de fotones en analogía con el número bariónico, pero incierto.
Es posible que al interaccionar tan poco, neutrinos y antineutrinos escaparan a la aniquilación mutua y actualmente existen en número parecido al número de fotones.
5. Los tres primeros minutos
En este capítulo se presenta una evolución de los tres primeros minutos del universo a partir de la primera centésima de segundo. Antes de ese instante la temperatura era superior a un billón y medio de Kelvin y el universo contendría grandes cantidades de mesones pi que impiden obtener una imagen clara de ese periodo de tiempo.
Cronológia del Big Bang
0.02s, 1011K, 8.6MeV, Densidad 4 x 109
"El universo es en su mayoría radiación (fotones) ... fue la luz la que luego formó el constituyente dominante del universo, y la materia ordinaria jugó solo el papel de un contaminante insignificante".
El universo es más simple y fácil de describir de lo que volverá a serlo en el futuro. Una sopa indiferenciada de materia y radiación en equilibrio térmico casi perfecto y cuya evolución posterior, por tanto, no depende de lo que ocurrió antes. Las magnitudes conservadas (carga, numero bariónico, número leptónico son muy pequeñas o nulas).
El universo es tan denso que hasta los neutrinos se mantienen en equilibrio térmico mediante rápidas colisiones con electrones, positrones y fotones.
El universo es más simple y fácil de describir de lo que volverá a serlo en el futuro. Una sopa indiferenciada de materia y radiación en equilibrio térmico casi perfecto y cuya evolución posterior, por tanto, no depende de lo que ocurrió antes. Las magnitudes conservadas (carga, numero bariónico, número leptónico son muy pequeñas o nulas).
El universo es tan denso que hasta los neutrinos se mantienen en equilibrio térmico mediante rápidas colisiones con electrones, positrones y fotones.
Electrones y positrones fueron creados a partir de la luz (producción de pares) y destruidos por aniquilación a tasas aproximadamente iguales. También existen partículas sin masa como fotones, neutrinos y antineutrinos. El umbral de producción de pares es de 1 MeV, por lo que la energía térmica kT = 8,6 MeV estaba muy por encima de eso, comportándose las partículas de materia como diferentes formas de radiación.
Los protones y los neutrones se transforman unos en otros al mismo ritmo mediante colisiones con electrones, positrones, etc porque el número leptónico es muy pequeño (mismos electrones que positrones y neutrinos que antineutrinos). Por lo tanto, el equilibrio exige que en el primer fotograma el número de protones sea similar al de neutrones. La diferencia de energía entre el neutrón y el protón es de 1.29 MeV, por lo que los protones se pueden transformar libremente en neutrones a esta temperatura. Solo hay alrededor de un barión para 109 fotones, como se deduce de las estimaciones del fondo cósmico de microondas y de su temperatura de 3K. Dado que la conservación del número de bariones es un fuerte principio de conservación, se infiere que la relación de fotones a bariones es constante durante todo el proceso de expansión.
Los núcleos atómicos se destruyen tan rápido como se crean debido a que la energía necesaria (6-8millones de eV) es inferior a la asociada a la temperatura del universo.
Los núcleos atómicos se destruyen tan rápido como se crean debido a que la energía necesaria (6-8millones de eV) es inferior a la asociada a la temperatura del universo.
0.11s, 3x1010K 2.6MeV, Densidad 30,000,000
Los neutrones libres se descomponen en protones, por lo que comienza a haber un exceso de protones sobre neutrones. Hay un 62% de protones y un 38% de neutrones. Sigue sin crearse núcleos atómicos.
El universo sigue en equilibrio térmico y todo muy por encima de su umbral de temperatura. Por tanto la densidad de energía ha disminuido con la cuarta potencia de la temperatura.
El universo sigue en equilibrio térmico y todo muy por encima de su umbral de temperatura. Por tanto la densidad de energía ha disminuido con la cuarta potencia de la temperatura.
1.09s, 1010K, 860KeV, Densidad 400,000
La bola de fuego primaria se vuelve transparente para los neutrinos, por lo que estos se liberan y ya no están en equilibrio térmico con los fotones, electrones y positrones. Se presume que el universo está lleno con un fondo de esos neutrinos ahora además del fondo de microondas de 3K de radiación electromagnética. Puesto que se lanzaron antes, la temperatura calculada es más baja, aproximadamente 2K. Si se consiguiera detectar este fondo cósmico de neutrinos con esa temperatura, se demostraría por ejemplo que el número leptónico es efectivamente bajo.
La materia en expansión todavía es opaca a la luz y a la radiación electromagnética de todas las longitudes de onda, por lo que están contenidas. Por tanto la densidad de energía sigue disminuyendo con la cuarta potencia de la temperatura, que es solo el doble de la temperatura umbral de electrones y positrones.
La materia en expansión todavía es opaca a la luz y a la radiación electromagnética de todas las longitudes de onda, por lo que están contenidas. Por tanto la densidad de energía sigue disminuyendo con la cuarta potencia de la temperatura, que es solo el doble de la temperatura umbral de electrones y positrones.
Por eso la aniquilación de positrones y de electrones ahora avanza más rápido que la producción de pares. Sigue siendo la temperatura demasiado elevada para que se formen núcleos atómicos estables pero su descenso permite que el balance protón-neutrón sea de 76% de protones y de 24% de neutrones.
Tiempo: 13.82 s, temperatura: 3x109K, 260KeV
Por debajo del umbral de producción de pares, el número de electrones y positrones disminuye rápidamente. Esta energía liberada ha retrasado la velocidad a la que el universo se enfria. Núcleos como 4He podrían formarse, pero no lo hacen debido al "cuello de botella de deuterio": el deuterio no es estable a esta temperatura con lo que no se pueden realizar el resto de reacciones (deuterio a He3 o tritio y de ahí a He4 que ya sería estable a la temperatura del cuarto fotograma. Los neutrones aún se convierten en protones, aunque mucho más lentamente. El balance es de 83% de protones y 17% de neutrones.
Tiempo: 3 min 2 s, temperatura: 109 K, 86KeV
Los electrones y los positrones casi han desaparecido. La energía liberada por estas aniquilaciones hace que la temperatura de los fotones sea un 35 por ciento mayor que la de los neutrinos (3K vs 2K)
Los fotones, los neutrinos y antineutrinos son los principales constituyentes del universo. Prácticamente no hay colisiones de electrones, positrones y neutrinos con neutrones, con lo que la transformación de estos en protones se produce por desintegración radiactiva (cada 100s la mitad de neutrones libres se convierte en protones). La descomposición de los neutrones deja un 86% de protones y un 14% de neutrones, pero estos representan una pequeña fracción de la energía del universo. La temperatura es suficientemente baja para que se mantengan unidos los núcleos de He3, tritio y He4 pero no de deuterio, con lo que sigue este cuello de botella. La abundancia de hidrógeno y helio del universo presente es un reflejo del equilibrio de las poblaciones de partículas establecidas en esta época temprana.
Tiempo: 3min46s Temperatura: 0.9x109K, 78KeV
El deuterón ahora es estable, por lo que todos los neutrones se combinan rápidamente para formar deuterio y luego núcleos de helio (las partículas alfa altamente estables) ya que nucleos con 5 u ocho partículas no son estables. No hay más decaimiento de neutrones ya que son estables en los núcleos con lo que el balance protón-neutrón apenas varia (86% de protones y un 14% de neutrones). El helio supone alrededor del 26% en masa en el universo desde esta época temprana. La proporción en peso del helio tras la nucleosíntesis es el doble de la proporción de neutrones respecto al resto de partículas nucleares, es decir, del 26% porque casi todos los neutrones están ligados al helio. Si la densidad de partículas fuera un poco mayor, la nucleosíntesis hubiera comienzado un poco antes cuando aun no se habían desintegrado tantos neutrones, con lo que se hubiera producido un poco más de helio pero no más del 28%. Nada más pesado se forma ya que no hay un producto estable con masa 5.
La temperatura precisa en la que se resuelve el atasco de deuterio y se forman los núcleos de helio depende ligeramente del número de partículas nucleares por fotón porque una densidad elevada de partículas hace un poco más fácil la formación de núcleos. Para 1000 millones de fotones por partícula nuclear, la nucleosíntesis comenzará a 900 millones de Kelvin tras 3min46s.
La temperatura precisa en la que se resuelve el atasco de deuterio y se forman los núcleos de helio depende ligeramente del número de partículas nucleares por fotón porque una densidad elevada de partículas hace un poco más fácil la formación de núcleos. Para 1000 millones de fotones por partícula nuclear, la nucleosíntesis comenzará a 900 millones de Kelvin tras 3min46s.
Si el proceso de expansión hubiera avanzado más lentamente, casi todos los neutrones se habrían descompuesto y el universo no habría podido formar átomos tal como los conocemos.
Tiempo: 34min40s, Temperatura: 3x108 K, 26KeV, Densidad 10
Los procesos nucleares se detienen (tenemos núcleos de helio y protones libres, es decir, núcleos de hidrógeno, la expansión y el enfriamiento continúan. Aproximadamente salvo 1 de cada 109 electrones se aniquiló con un positrón debido a un ligero exceso de electrones sobre los positrones en la bola de fuego primigenia. Lo justo para equilibrar la carga de los protones. Hay un electrón por protón pero el universo está demasiado caliente para que se formen átomos estables. La razón del exceso de materia sobre la antimateria es una investigación continua. La densidad de energía de la radiación es de aproximadamente 69% de fotones y un 31% de neutrinos. La temperatura de los fotones es un 40% mayor que la de los neutrinos.
700000 años, 3000K, 0,26eV
El universo se siguió enfriando durante 700.000 años sin que ocurriera nada relevante. En este punto el universo está lo suficientemente frío para que los núcleos de hidrógeno y helio recojan electrones y se conviertan en átomos estables. La ausencia de gas ionizado hace que el universo sea transparente a la luz por primera vez.
A 3000 K, tenemos que kT = 0,26 eV, por lo que por encima de esta temperatura, la formación del átomo se ve obstaculizada porque es en este pun punto en que pudieron comenzarse a crear.
Antes del punto de los 700.000 años, los iones y los electrones del plasma eran dispersores de luz eficientes, pero después de que se condensaran en átomos, son dispersores de luz muy ineficientes.
A partir de este momento, la radiación se desacopló de la materia, permitiendo a esta comenzar a crear galaxias y estrellas mediante la atracción gravitatoria, y continuó enfriándose a medida que la expansión cosmológica la desplazaba hacia el rojo. Con el descubrimiento de la radiación de fondo de 3K, ahora observamos el remanente de la radiación que se liberó en este punto de transparencia. De hecho, la medida de las características de esta radiación cósmica de fondo proporcionó una de las partes clave del modelo de big bang.
Actualmente sabemos que las estrellas están formadas por helio entre un 20% y un 30%, lo que sería consistente con este relato que se apoya en la temperatura de 3K del fondo cósmico de microondas para estimar el número de 1000 millones de fotones por partícula nuclear.
Sobre este relato habría la incertidumbre de si el universo primitivo fue homogéneo e isótropo como se ha supuesto y como lo es una vez se hizo transparente a la radiación, ya que el fondo cósmico de microondas es bastante homogéneo e isótropo.
6. Una disgresión histórica
La detección del fondo cósmico de microondas fue uno de los descubrimientos científicos más importantes del siglo XX, pero, ¿por qué no hubo una búsqueda sistemática de esa radiación mucho antes de 1965?
Con las proporciones de helio e hidrógeno observadas se hubiera podido inferir que la nucleosintesis debió comenzar cuando la proporción de neutrones entre las partículas nucleares disminuyó del 10 al 15%. Y la proporción de neutrones alcanzó ese valor cuando el universo estaba a una temperatura de unos 1000 millones de Kelvin.
Esto permitiría hacer una estimación aproximada de la densidad de partículas nucleares a esa temperatura, mientras que la densidad de fotones a esa temperatura puede calcularse mediante las propiedades de la radiación del cuerpo negro. Con eso podía conocerse la proporción entre el número de fotones y el número de partículas nucleares, que no cambia con el tiempo.
Partiendo de la densidad actual de partículas nucleares, se podría conocer la densidad actual de fotones e inferir la existencia de un fondo cósmico de microondas con una temperatura actual de entre 1 y 10K. Pero nadie hizo esta predicción siguiendo este razonamiento.
Esto permitiría hacer una estimación aproximada de la densidad de partículas nucleares a esa temperatura, mientras que la densidad de fotones a esa temperatura puede calcularse mediante las propiedades de la radiación del cuerpo negro. Con eso podía conocerse la proporción entre el número de fotones y el número de partículas nucleares, que no cambia con el tiempo.
Partiendo de la densidad actual de partículas nucleares, se podría conocer la densidad actual de fotones e inferir la existencia de un fondo cósmico de microondas con una temperatura actual de entre 1 y 10K. Pero nadie hizo esta predicción siguiendo este razonamiento.
La predicción de un fondo cósmico de microondas se hizo en 1948 en un artículo de George Gamow, Ralph Alpher y Robert Herman que desgraciadamente no indujo a su búsqueda. Aunque sus calculos no eran del todo correctos predijeron un fondo de radiación de 5K. Pero quienes conocian esta predicción no lo dieron importancia. Además es sorprendente que no hubiera más estudios teóricos similares hasta alrededor de 1965 cuando ya prácticamente se había descubierto.
Las proporciones de hidrógeno y helio actuales requerían un fondo de radiación cósmica que podía ser observado en la actualidad. El hidrógeno no se crea en las estrellas sino que es su combustible inicial. Si el universo contiene un 75% de hidrógeno, entonces debió existir un fondo de fotones que impidiera que el hidrógeno se transformara en helio y otros elementos más pesados.
7. La primera centésima de segundo
El primer fotograma de los tres primeros minutos del universo comenzaba a una temperatura de 100.000 millones de Kelvin (inferior a la temperatura umbral de todos los hadrones), y las únicas partículas presentes eran fotones, electrones, neutrinos y sus correspondientes antipartículas.
Pero para temperaturas superiores debe haber habido gran cantidad de hadrones en equilibrio térmico y en continua interacción que no sabemos describir con precisión suficiente para realizar predicciones precisas. El motivo es su interacción mediante la fuerza nuclear fuerte (los leptones no lo hacen), a la que no puede aplicarse la teoría de perturbaciones tan fácilmente como a la QED porque la constante de acoplamiento es cercana a la unidad, mientras que en la QED es 0,0073.
Aún así podría hacerse algunos cálculos considerando la propiedad de libertad asintótica de los quarks que forman los hadrones. Esta propiedad de las teorías gauge no abelianas como la cromodinámica cuántica hace que la fuerza de color entre quarks tienda a anularse cuando estos están muy juntos, como pudo suceder en los primeros instantes del universo.
Pero para temperaturas superiores debe haber habido gran cantidad de hadrones en equilibrio térmico y en continua interacción que no sabemos describir con precisión suficiente para realizar predicciones precisas. El motivo es su interacción mediante la fuerza nuclear fuerte (los leptones no lo hacen), a la que no puede aplicarse la teoría de perturbaciones tan fácilmente como a la QED porque la constante de acoplamiento es cercana a la unidad, mientras que en la QED es 0,0073.
La constante de estructura fina es el parámetro fundamental del electromagnetismo y también la constante de acoplamiento de la QED
Lagrangiana de la Electrodinámica Cuántica, la teoría que describe como interacciona la luz con la materia. M es la masa del electrón, A es el potencial vector del electromagnetismo y F es el tensor electromagnético. Los dos primeros corresponden a la ecuación de Dirac, el tercero es el de interacción entre el electrón y el fotón (consecuencia de la simetría gauge) y el cuarto es el de la propagación del fotón en ausencia de fuentes (onda electromagnética)
Aún así podría hacerse algunos cálculos considerando la propiedad de libertad asintótica de los quarks que forman los hadrones. Esta propiedad de las teorías gauge no abelianas como la cromodinámica cuántica hace que la fuerza de color entre quarks tienda a anularse cuando estos están muy juntos, como pudo suceder en los primeros instantes del universo.
Otro de los problemas tiene que ver con una transición de fase asociada con las interacciones débiles (responsable de la desintegración del neutrón y de las interacciones que involucran neutrinos) que habría ocurrido cuando la temperatura descendió por debajo de los 3000 billones de Kelvin.
A una temperatura superior esta interacción estaría unificada con la electromagnética y descrita por la teoría electrodébil (también gauge no abeliana). Al descender la temperatura por debajo de ese umbral, esta simetría se rompió (aunque sigue escondida en las ecuaciones de la teoría).
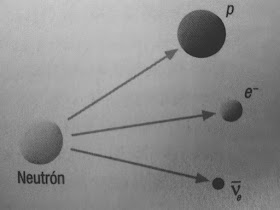
La fuerza nuclear débil es la responsable de la desintegración beta en la que un neutrón se transforma en un protón más un electrón más un antineutrino
Diagrama de Feynman de la desintegración beta en la que un bosón W se lleva una unidad negativa de carga y se acaba desintegrando en un electrón y un antineutrino.
A una temperatura superior esta interacción estaría unificada con la electromagnética y descrita por la teoría electrodébil (también gauge no abeliana). Al descender la temperatura por debajo de ese umbral, esta simetría se rompió (aunque sigue escondida en las ecuaciones de la teoría).
A la izquierda el potencial de Higgs es nulo cuando el campo de Higgs también lo es. Sin embargo a la derecha se rompe esta simetría y el potencial es diferente de cero cuando el campo de Higgs es nulo
Respecto a la débil fuerza de la gravedad, esta podría haber influenciado la evolución del universo primitivo cuando la temperatura fue de 1032 (temperatura de Planck) cuyo umbral se atravesó en el tiempo de Planck (10-43).
A la temperatura de Planck la densidad de energía era tan grande que sus efectos gravitatorios tuvieron que ser importantes. Sin embargo los desconocemos porque no disponemos de una teoría de gravedad cuántica, a la que la teoría M es una de las candidatas actuales.
Pero esto no afecta el relato del universo primitivo a partir del primer segundo porque este viene determinado por el equilibrio térmico en el que las cantidades y distribuciones de todas las partículas viene determinada por las leyes de la mecánica estadística.
La temperatura de Planck es de 1032K y era la temperatura aproximada en el tiempo de Planck
A la temperatura de Planck la densidad de energía era tan grande que sus efectos gravitatorios tuvieron que ser importantes. Sin embargo los desconocemos porque no disponemos de una teoría de gravedad cuántica, a la que la teoría M es una de las candidatas actuales.
Las dualidades debil-fuerte y radio grande-pequeño crean una red de conexiones que interrelacionan y fusionan las cinco teorías de cuerdas, la supergravedad en once dimensiones y la Teoría M en un marco unificado.
La dualidad grande/pequeño del radio completa la red de conexiones resultando que las cinco teorías de cuerdas, junto con la Teoría M, son duales entre sí. Las diferentes teorías de supercuerdas son en el fondo soluciones particulares de una teoría más profunda llamada teoría M
Pero esto no afecta el relato del universo primitivo a partir del primer segundo porque este viene determinado por el equilibrio térmico en el que las cantidades y distribuciones de todas las partículas viene determinada por las leyes de la mecánica estadística.
Hay una excepción: las ondas gravitacionales, que se desplazan a la velocidad de la luz. La radiación gravitacional habría salido del equilibrio térmico mucho antes, cuando la temperatura fue de en torno a 1032K. Desde entonces su temperatura ha disminuido en proporción inversa al tamaño del universo, siendo su temperatura actual aproximadamente de 1K.
La fusión de dos agujeros negros genera ondas gravitacionales
8. Epílogo: la perspectiva futura
Si el universo continua expandiéndose eternamente como parece que muestran los datos astronómicos, entonces las reacciones termonucleares en las estrellas se acabarán, dejando tras de sí enanas blancas, estrellas de neutrones y agujeros negros.
Los planetas seguramente continúen en órbita, disminuyendo ligeramente su velocidad y el radio de su órbita a medida que irradien ondas gravitacionales pero sin llegar nunca al reposo en un tiempo finito.
El espacio-tiempo se curva de manera extrema en un agujero negro
Los planetas seguramente continúen en órbita, disminuyendo ligeramente su velocidad y el radio de su órbita a medida que irradien ondas gravitacionales pero sin llegar nunca al reposo en un tiempo finito.
Las órbitas de los planetas del Sistema Solar fueron descritas por primera vez por la Ley de Gravitación Universal
Los fondos cósmicos de radiación y de neutrinos seguirán reduciendo su temperatura en proporción inversa al tamaño del universo, pero nunca faltaran.
Opinión personal
Este libro me parece una gran introducción a la cosmología por su sencillez y la capacidad didáctica de su autor. Explica de forma muy comprensible los principios físicos (radiación del cuerpo negro, efecto Doppler) y los descubrimientos astronómicos (ley de Hubble y expansión del universo, fondo cósmico de microondas) necesarios para reconstruir cómo pudo ser el universo primitivo, es decir, el universo antes de que se hiciera transparente a la radiación.











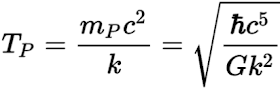





Very good article,Thank you
ResponderEliminarFor sofa renovation contact thesofastore they gives bestSofa Refurbishing in Dommasandra,Bangalore