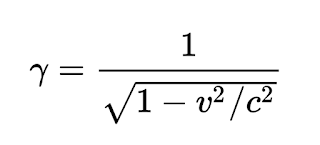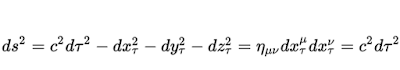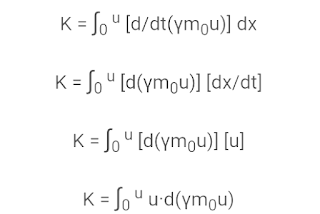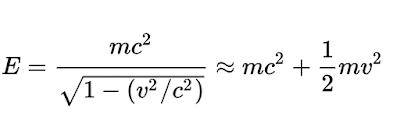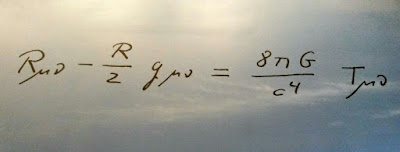A continuación quería compartir un resumen y mi opinión personal del fantástico libro ¿Por qué E=mc2?¿Y por qué debería importarnos? Escrito por Brian Cox y Jeff Forshaw.
Índice
1) Espacio y tiempo.
2) La velocidad de la luz.
3) Relatividad Especial.
4) Espacio-tiempo.
5) ¿Por qué E=mc2?
6) ¿Y por qué debería importarnos? Sobre átomos y la energía de las estrellas.
7) El Origen de la masa.
8) La curvatura del espacio-tiempo.
E=mc2 es probablemente la ecuación más famosa de la física
1) Espacio y tiempo
El principio de relatividad de Galileo nos dice que no hay espacio absoluto pues no hay experimento que permita saber si nos estamos moviendo en ausencia de fuerzas.
Si no hay espacio absoluto dos observadores pueden no estar de acuerdo en el tamaño de un objeto.
Por otro lado la idea de un tiempo absoluto entra en contradicción con el concepto de movimiento relativo. Los experimentos de Faraday sobre inducción electromagnética solucionaron esta contradicción al evidenciar que no existe un tiempo absoluto. Otro de los grandes méritos de Faraday fue la introducción del concepto de campo para explicar la acción a distancia del electromagnetismo.
Que el espacio y el tiempo sean relativos puede chocar con el sentido común, pero son afirmaciones que han superado el método científico a diferencia de los conceptos absolutos.
2) La velocidad de la luz
Las Ecuaciones de Maxwell
Maxwell unificó los conocimientos de electricidad y magnetismo obtenidos de los experimentos de Faraday, Ampére y Gauss en las Ecuaciones de Maxwell.
Las Ecuaciones de Maxwell
Además de esta unificación el otro gran logro de Maxwell fue la introducción de la corriente de desplazamiento que posteriormente permitió llegar a la ecuación de onda electromagnética.
Ecuación de Onda Electromagnética. Tanto el campo eléctrico como el campo magnético se propagan como una onda a la velocidad de la luz
Las ecuaciones de Maxwell están escritas en el lenguaje de los campos porque no tenía otra opción. Además relacionan las causas (cargas y corrientes) con sus efectos (los campos electrico y magnético).
A partir de sus ecuaciones, Maxwell fue capaz de deducir de ellas la ecuación de onda electromagnética. Esta ecuación muestra que la luz se mueve a velocidad constante independientemente de la velocidad de la fuente y el observador.
La constancia de la velocidad de la luz fue demostrada por el experimento de Michelson-Morley y su independencia de la fuente y el observador implica que no hay un tiempo absoluto.
La luz puede propagarse en el vacío porque está generada por la oscilación de campos eléctrico y magnético que se inducen mutuamente.
La Teoría de la Relatividad Especial
A partir de los conceptos relativos del espacio y el tiempo y de las Ecuaciones de Maxwell Einstein estableció los dos postulados de la Relatividad Especial:
1) La luz se mueve a una velocidad constante c independientemente de la fuente y el observador.
2) El Principio de Relatividad y la imposibilidad de determinar el movimiento absoluto.
En la Relatividad Especial hay 3 conceptos fundamentales:
- La invariancia: La teoría debe ser independiente del estado de movimiento del observador. Por tanto debe basarse en magnitudes invariantes. Por ejemplo, el espacio y el tiempo por separado no son invariantes, pero el espacio-tiempo sí lo es.
- La causalidad: La constancia de la velocidad de la luz y su valor finito implica el concepto de cono de luz y la desconexión causal de dos sucesos que impliquen una velocidad superior para comunicarse. Además implica también el fin de la simultaneidad.
- La distancia: Hay que definir una distancia invariante en el espacio-tiempo que sea causal. Es decir, que si para un observador un suceso es previo a otro, esto sea así para cualquier observador de ambos sucesos independientemente de su estado de movimiento.
3) Relatividad Especial
A partir de los 2 postulados de la Relatividad Especial Einstein siguió el método científico para extraer consecuencias y predicciones comprobables mediante experimentos reales o mentales.
Un experimento mental para mostrar que el tiempo es relativo es la observación de un rayo de luz a través de un tren por parte de un observador sentado en el vagón y por otro desde el andén.
Dos observadores miden tiempos diferentes debido a su movimiento relativo y a la constancia de la velocidad de la luz
Cálculo de la dilatación del tiempo en Relatividad Especial debido al movimiento relativo
Como la velocidad de la luz es constante, el tiempo transcurre más despacio para el pasajero del tren que para el observador desde el andén porque la luz debe recorrer una distancia mayor.
En el caso hipotético (físicamente imposible) que el tren viajara a la velocidad de la luz, el observador en el anden tendría que esperar un tiempo infinito a que el rayo de luz llegara al extremo inferior de la ventana, mientras que para el observador en el tren no.
La relación entre los intervalos de tiempo medidos por ambos observadores es conocido como el factor gamma:
Factor gamma en la Relatividad Especial
Es decir,
t2=γt1
El tiempo va a ritmos diferentes en función del movimiento relativo. La medida del tiempo se hace a través del espacio (péndulo, reloj de luz, ...) y por eso el movimiento afecta al transcurrir del tiempo.
Un experimento real es medir el tiempo de vida media de una partícula inestable como el muón. En reposo vive 2,2 microsegundos. Pero si se mueve en un acelerador de partículas a 0,9994c vive 60 microsegundos, es decir, 29 veces más.
El muón es una de las partículas elementales del Modelo Estándar
En la dirección del movimiento las longitudes se contraen. Si nos movieramos con el muón, su vida media sería de 2,2 microsegundos porque estaríamos en reposo con respecto al muón. Sin embargo, el muón daría las mismas vueltas porque la longitud del anillo se reduce para el muón.
4) Espacio-tiempo
Los físicos buscan descubrir propiedades invariantes del Universo porque conducen a revelaciones reales y tangibles.
Las ecuaciones más interesantes son aquellas capaces de proporcionar una descripción de la naturaleza con la que todo el mundo esté de acuerdo. Ecuaciones donde solo aparezcan magnitudes invariantes. Como ahora la distancia y el tiempo por separado no son invariantes, la ecuación v=x/t no es muy útil.
Pero se puede conjeturar que el espacio y el tiempo se combinan en una entidad, el espacio-tiempo, en que las distancias son invariantes. Deberemos buscar una definición de distancia que no varíe en función del movimiento relativo de los observadores.
Definición de distancia
La causalidad implica restricciones en la estructura del espacio-tiempo porque los eventos conectados causalmente no pueden invertirse independientemente del movimiento del observador.
También hay que considerar que la dimensión temporal y las dimensiones espaciales no se comportan igual. En la primera siempre nos movemos en una dirección. En el espacio podemos movemos en cualquier dirección.
El espacio se mide en metros y el tiempo en segundos.¿Cómo podemos combinarlos? Utilizando una velocidad de conversión que llamaremos c, para convertir segundos en metros: x=ct.
Las dos opciones más sencillas para definir una distancia en el espacio-tiempo son (caso sencillo de una dimensión temporal y una espacial):
1) s2=(ct)2 + (x)2
2) s2=(ct)2 - (x)2
En formato diferencial para distancias infinitesimales:
1) ds2=(cdt)2 + (dx)2
2) ds2=(cdt)2 - (dx)2
En el caso de la suma sería una distancia euclídea (donde es válido el Teorema de Pitágoras) mientras que en el caso de la resta sería una distancia correspondiente a una geometría plana no euclídea (hiperbólica).
A la izquierda un espacio-tiempo euclídeo donde es válido el teorema de Pitágoras. A la derecha un espacio-tiempo hiperbólico, el de la Relatividad Especial
El caso euclídeo debe descartarse porque no conserva la causalidad. En función del movimiento del observador, dos sucesos separados una determinada distancia, que al ser un invariante es la misma para todos los observadores, podrían ocurrir en un orden diferente. Por tanto la imposición de la causalidad implica que el espacio-tiempo de la Relatividad Especial es plano pero no euclídeo.
Espacio-tiempo de Minkowski de 2 dimensiones. Los ejes negros son los correspondientes a un observador en reposo y los azules a un observador en movimiento relativo. La inclinación de los ejes azules depende de la velocidad relativa. Si el observador se moviera a v=c, los ejes azules se convertirían en uno solo porque X'=cT'
Si x=ct, entonces la distancia entre dos sucesos es nula. Si x fuera mayor que ct, tendríamos una distancia negativa en el espacio-tiempo, cosa que físicamente no tendría sentido. Por tanto, si x=ct, la velocidad c es un limite de velocidad cósmico. Protege la causalidad al evitar distancias negativas.
Además, si todos los observadores deben medir la misma distancia s, también han de estar de acuerdo en el límite de velocidad cósmico c, con lo que c es también un invariante.
Aplicando esta definición de distancia en el espacio-tiempo de Minkowski al ejemplo del tren del tercer capítulo podemos llegar al mismo resultado únicamente con consideraciones geométricas.
El observador sentado en el tren puede pensar que está en reposo. Por tanto x1 es cero. Para el observador en el andén el tren recorre una distancia x1 = vt2. Por tanto:
- Observador en el tren: s2=(ct1)2
- Observador en andén: s2=(ct2)2-(vt2)2
Como la distancia definida es un invariante (las transformaciones de Lorentz no la modifican), ambos observadores deben medir la misma distancia:
(ct1)2=(ct2)2-(vt2)2
t2=γt1
que es lo mismo que habíamos obtenido en el capítulo 3.
Las Transformaciones de Lorentz mantienen invariante el intervalo relativista y permiten obtener las coordenadas de un suceso para diferentes observadores
Tiempo Propio
El observador del tren considera que él está en reposo al no moverse respecto al vagón. Por ello a su tiempo t1 , es decir al tiempo medido por un reloj comóvil, se le llama tiempo propio y se designa por la letra τ. Al tiempo del otro observador se le asigna la letra t:
t = γτ
En notación diferencial para intervalos de tiempo muy pequeños:
dt = γdτ
En el espacio-tiempo todo viaja a velocidad c, aunque estés en reposo en el espacio porque sigues avanzando en el tiempo. El movimiento en el espacio es la sombra de un movimiento más universal en el espacio-tiempo. Si te mueves en el espacio, entonces debes moverte más lentamente en el tiempo para mantener la velocidad c. Por eso para un observador en movimiento el tiempo pasa más despacio. De hecho un reloj en reposo marca el tiempo lo más rápido posible.
Sabiendo que la distancia es:
ds2=(cdt)2-(dx)2
Para un observador en reposo o con un reloj moviéndose con él, tenemos que dx=0. En este caso, como hemos comentado el tiempo se denomina tiempo propio y se designa con la letra τ, con lo que:
Intervalo relativista en función del tiempo propio
El tiempo propio es un invariante relativista pues es el cociente de dos invariantes. El tiempo propio mide la distancia recorrida en el espacio-tiempo
En 4 dimensiones, el intervalo relativista o distancia se generaliza como:
Intervalo relativista para un espacio-tiempo de 4 dimensiones
En función del tiempo propio:
Intervalo relativista en función del tiempo propio
Métrica de la Relatividad Especial para un espacio-tiempo de 4 dimensiones necesaria para calcular la distancia entre dos sucesos
5) ¿Por qué E=mc2?
Desde el punto de vista del espacio-tiempo todo se mueve a velocidad c. En el caso concreto de la luz, se mueve a velocidad c en el espacio y nula en el tiempo (un fotón no envejece). Por tanto en el espacio viaja a la velocidad que marca el límite cósmico. Esto es así porque la masa del fotón es nula.
Desde el siglo XII se ha comprobado que las ecuaciones fundamentales de la física son invariantes. Es decir, las leyes de la física deben expresarse mediante cantidades invariantes.
Para llegar a E=mc2 necesitamos más invariantes además de la distancia espacio-tiempo, la velocidad de la luz y el tiempo propio. Necesitamos los vectores tetradimensionales posición, velocidad y momento lineal, también conocidos como cuadriposición, cuadrivelocidad y cuadrimomento.
Debemos encontrar los cuadrivectores invariantes como generalización de sus esquivalentes tridimensionales para llegar a la famosa ecuación de Einstein de equivalencia entre masa y energía.
- Cuadriposición:
X = (ct, x, y, z)
dX·dX= ds2 = (cdt)2 - (dx)2 - (dy)2 - (dz)2
La primera componente de la cuadriposición en notación diferencial es cdt (el tiempo por un factor de conversión invariante que lo transforme en metros) y las otras 3 son las equivalentes a las coordenadas espaciales de un espacio de 3 dimensiones. Su norma al cuadrado es el intervalo relativista o distancia al cuadrado (invariante), que se calcula aplicando la métrica mostrada en el capítulo anterior:
ds2 = (cdt)2 - (dx)2 - (dy)2 - (dz)2
- Cuadrivelocidad:
Cuadrivelocidad en Relatividad Especial, siendo u la velocidad en el espacio tridimensional
La cuadrivelocidad se define como la variación de la cuadriposición respecto al tiempo propio. Al ser un cociente de dos invariantes, es también un invariante, siendo su norma la velocidad de la luz. Esto es coherente con lo que habíamos comentado que en el espacio-tiempo todo se mueve a la velocidad de la luz.
Cuadrivelocidad en Relatividad Especial
- Cuadrimomento:
Cuadrimomento en Relatividad Especial
El cuadrimomento se define como el producto de dos invariantes: la masa en reposo al ser una propiedad intrínseca de un cuerpo y la cuadrivelocidad. Por eso será también un invariante.
Módulo al cuadrado del cuadrimomento
El módulo del cuadrimomento es el invariante m0c, coherente con el hecho de que en el espacio-tiempo siempre nos movemos a la velocidad de la luz.
Para obtener una expresión de la energía relativista es conveniente partir de la definición de energía cinética como el trabajo de una fuerza necesario para aumentar la velocidad desde 0 hasta u:
Energía Cinética como trabajo de una fuerza
Considerando que las componentes espaciales de la cuadrifuerza en Relatividad son la variación del cuadrimomento respecto del tiempo tenemos que:
Si la velocidad es nula, entonces γ=1 con lo que la energía cinética K también es cero. Por tanto hemos llegado a un definición consistente.
Si consideramos m0c2 la energía en reposo y K la energía cinética, entonces podemos definir la energía total E como:
E = γm0c2 = K + m0c2 = mc2
E=mc2 es la ecuación más famosa de la física
A bajas velocidades, es decir, cuando v es mucho menor que c, el factor gamma puede aproximarse por una serie polinómica resultando una energía intrínseca del objeto más la energía cinética clásica:
Aproximación de la energía relativista a bajas velocidades (cuando v es mucho menor que c)
En notación más compacta y usando m0 para la masa en reposo:
E = γm0c2 ~ m0c2 + ½m0v²
Aplicando la definición de energía E = γm0c2 a la componente temporal del cuadrimomento obtenemos:
Relación entre cuadrimomento y energía en Relatividad Especial
Calculando el módulo al cuadrado del cuadrimomento y operando obtenemos una expresión alternativa para la energía total, especialmente útil para el caso de partículas sin masa:
Energía en función del momento en Relatividad
Resultando la ecuación:
Energía en función del momento. Esta ecuación es usada sobretodo en Mecánica Cuántica Relativista
Para una partícula en reposo (p=0), obtenemos la famosa ecuación de Einstein E=m0c2. En el caso de que la masa sea nula, como para el fotón, entonces:
E=pc
Como consecuencia la masa puede convertirse en energía cinética y viceversa siempre que la suma de ambas se conserve. La masa es una medida de la energía latente acumulada en la materia. Por tanto, la energía que podemos obtener de una masa en reposo es E=m0c2.
Antes de la Teoría de la Relatividad masa y energía parecían magnitudes inconexas. Ahora la energía, la masa y el momento son manifestaciones diferentes de lo mismo y se combinan en un mismo objeto del espacio-tiempo: el cuadrimomento. Esta entidad se manifiesta como energía en el tiempo y como momento en el espacio.
Si un objeto tiene masa nula podemos dividir la energía entre el momento para obtener E=pc considerando que una partícula de masa nula se mueve en el espacio a la velocidad de la luz c. Es decir, una partícula de masa nula tiene momento y energía solo si se mueve a la velocidad de la luz, como es el caso de los fotones.
Si en el futuro se descubriera que los fotones tienen masa no nula, se tendría que modificar el segundo postulado de Einstein por: "la velocidad de las partículas sin masa es una constante universal". Ya no podríamos identificar el límite de velocidad cósmico con la velocidad de la luz, que ya no apareceria en E=mc2.
6) ¿Y por qué debería importarnos? Sobre átomos y la energía de las estrellas.
La materia acumula una energía descomunal debido al valor elevado de c. Nosotros hemos aprendido a extraerla en las centrales nucleares mediante la fisión nuclear. La naturaleza lleva aplicando E=mc2 desde siempre en las estrellas obteniendo la energía mediante la fusión nuclear.
La masa del átomo es menor que la de sus componentes porque descomponerlo cuesta energía. Esto sucede para los elementos químicos con un número atómico inferior al del hierro. Los núcleos más pesados que el hierro no liberarían energía al fusionarse. Por eso los elementos más pesados que el hierro no son tan abundantes, pues no pueden crearse en las estrellas. Se crean en pequeñas cantidades en las supernovas.
Según el Modelo del Big Bang, los primeros átomos de Hidrógeno y Helio se crearon mediante reacciones de fusión nuclear gracias a las elevadas temperaturas
Los núcleos más pesados que el hierro prefieren desprenderse de protones y neutrones, como el Uranio, dando lugar a reacciones de fisión. En estos casos, la suma de las masas de los núcleos resultantes es inferior al original, y por eso también puede liberarse energía.
La energía nuclear proporciona más energía que la obtenida de reacciones químicas (petróleo, carbón) porque la fuerza nuclear fuerte es mucho más intensa que la electromagnética.
Por ejemplo, la fusión de 2 protones proporciona 0,5MeV de energía mientras que la fusión de 2 átomos de hidrógeno y uno de oxígeno solo 6eV. Un millón de veces menos.
7) El Origen de la masa
La ecuación E=mc2 nos dice que la masa y la energía son equivalentes y que se pueden convertir una en la otra. Pero no nos dice mediante qué proceso esto ocurre. Eso nos lo dice la lagrangiana del Modelo Estándar de Partículas, una ecuación que sintetiza toda la física que conocemos salvo la relacionada con la gravedad.
Lagrangiana del Modelo Estándar de Partículas
Las dos últimas líneas de la Lagrangiana del Modelo Estándar son las que especifican como adquieren masa las partículas
Esta ecuación constituye el núcleo del Modelo Estándar y especifica las reglas mediante las que interactúan entre sí dos partículas cualesquiera salvo las de la gravedad. Una interacción entre un electrón y un fotón sería un ejemplo. En estas interacciones se convierte masa en energía y viceversa.
La ecuación anterior es compleja y los cálculos complicados. Los diagramas de Feynman permiten simplificar los cálculos de probabilidades de interacción entre dos partículas.
Diagrama de Feynman en que un electrón y un positrón se convierten en dos fotones (conversión de masa en energía) que posteriormente vuelven a convertirse en un par electrón-positrón
8) La curvatura del espacio-tiempo
La idea del espacio-tiempo nos ha conducido de forma natural a E=mc2. Lo modelamos como un espacio-tiempo de Minkowski, que es curvo en el sentido de no euclidiano, pero con curvatura constante. ¿Podría la curvatura variar de un punto a otro?
El camino hacia la Relatividad General parte de que todas las cosas caen al suelo con la misma aceleración. Esto es conocido como el principio de equivalencia. Este principio afirma que las leyes físicas son las mismas en un campo gravitatorio que en situación de movimiento acelerado. Por tanto podemos prescindir del concepto de gravedad y hablar de caída libre o movimiento acelerado.
El principio de equivalencia también afirma que a una escala suficientemente pequeña siempre podemos aproximar el espacio-tiempo existente por el de la Relatividad Especial, es decir, por un espacio-tiempo de Minkowski.
Uniendo los pequeños espacios de Minkowski podemos formar un espacio-tiempo curvo.
Las ecuaciones de la Relatividad General nos proporcionan la métrica del espacio-tiempo curvo a partir de la distribución de masa y energía existente
Es decir, podemos hacer que la gravedad desaparezca a costa de que el espacio-tiempo se curve, con lo que:
Gravedad = Curvatura
Curvatura del espacio-tiempo en el entorno de un agujero negro
Donde hay materia hay gravedad. Como masa y energía son equivalentes según E=mc2, donde hay energía también. Por tanto, materia y energía curvan el espacio-tiempo.
Los agujeros de gusano son soluciones extremadamente inestables de la Relatividad General. Permitirían conectar regiones lejanas del Universo al curvar drásticamente el espacio-tiempo
Opinión Personal
Seguramente es el mejor libro que he leído sobre la Teoría de la Teoría de la Relatividad Especial porque de la Teoría General de la Relatividad no habla mucho (solo le dedica el último capítulo).
Con las matemáticas imprescindibles explica como a partir de únicamente dos postulados y tres conceptos fundamentales (causalidad, invariancia y distancia) se debe sustituir la noción de espacio y tiempo separados por un nuevo ente: el espacio-tiempo. Y también de una manera comprensible se deduce la ecuación más famosa de la física: E=mc2.
Lo mejor de este libro es que para evitar un exceso de matemáticas se utiliza constantemente el razonamiento físico para ir llegando a las conclusiones mas importantes de la teoría. Esto permite al lector entender mejor los resultados de la Relatividad Especial aunque no sean muy intuitivos, como la dilatación del tiempo o la equivalencia entre masa y energía.