Este es un resumen del libro: "Sobre la Teoría de la Relatividad Especial y General" escrito por Albert Einstein hace ya algunas décadas. Es un libro muy interesante porque explica los fundamentos de la teoría sin entrar en el complicado aparato matemático necesario, sobre todo en la Relatividad General.
Puesto que está escrito hace bastantes años es posible que algunas de las afirmaciones realizadas por el autor no estén completamente vigentes, principalmente en cosmología.
Índice
Primera Parte
Sobre la Teoría de la Relatividad Especial
Geometría, Sistemas de Coordenadas, Espacio y Tiempo.
Aparente Incompatibilidad de los Postulados de la Relatividad Especial.La Relatividad de la Simultaneidad.
Las Transformaciones de Lorentz.
El Comportamiento de reglas y relojes en movimiento.
El Teorema de Adición de Velocidades.
La Relatividad de la Distancia Espacial.
Resumiendo las Ideas Clave de la Relatividad Especial.
Resultados Generales de la Teoría.
La Teoría de la Relatividad Especial y la Experiencia.
Espacio-tiempo Cuadridimensional de Minkowski.
Segunda Parte
Sobre la Teoría de la Relatividad General
El Campo Gravitatorio.
Ejemplo del Disco Giratorio.
Principio de Relatividad Generalizado.
La Solución del Problema de la Gravitación sobre la base del Principio de la Relatividad General.
Confirmación de la Relatividad General por la experiencia.
Cosmología
El Problema del Espacio
El Concepto de Campo.
El Concepto de Espacio en la Teoría de la Relatividad Especial.
El Concepto de Espacio en la Teoría de la Relatividad General.
Primera Parte
Sobre la Teoría de la Relatividad Especial
Geometría, Sistemas de Coordenadas, Espacio y Tiempo
La validez que otorgamos a los teoremas geométricos es debido a su identificación con la realidad física. Vemos que funcionan en nuestra vida cotidiana.
En la física experimental se utiliza normalmente el Sistema de Coordenadas Cartesianas, que es un sistema de paredes y reglas rígidas que se rigen por las leyes de la geometría euclídea y que nos permite asignar 3 números a un suceso para ubicarlo en el espacio.
La mecánica clásica tiene como objetivo describir como varía con el tiempo la posición de los cuerpos en el espacio. Pero esta posición tendrá que ser referida a un sistema de coordenadas concreto y el tiempo respecto a un reloj concreto.
Aunque la trayectoria real sea única, su descripción matemática puede variar en función del sistema de coordenadas al que es referida. La traducción entre trayectorias para comprobar que corresponden a una misma trayectoria física se realiza mediante las transformaciones de coordenadas.
Para cada trayectoria hay que especificar en que instante de tiempo se encuentra la partícula para poder describir como varía respecto al tiempo. Pero esto exige una definición de tiempo.
Un tipo de sistema de coordenadas es el de Galileo o inercial, que es aquel en el que es válido el Principio de Inercia de Galileo-Newton.
Cualquier sistema de coordenadas que se encuentre en movimiento rectilíneo uniforme respecto a un sistema de coordenadas de Galileo, también es un sistema de coordenadas de Galileo.
Aparente Incompatibilidad de los Postulados de la Relatividad Especial
Aparente Incompatibilidad de los Postulados de la Relatividad Especial
Respecto a los sistemas de Galileo o inerciales puede postularse el Principio de Relatividad: "las leyes físicas son las mismas para dos sistemas de referencia que se mueven entre sí con un movimiento rectilíneo uniforme."
Hasta ahora se ha comprobado que este principio se cumple con bastante exactitud. No obstante se sigue poniendo a prueba constantemente.
Además está sólidamente establecido que la velocidad de la luz es constante e igual para todas las frecuencias.
Las Leyes de Maxwell predicen una velocidad constante y finita para la luz
Según la mecánica clásica, el teorema de adición de velocidades afirma que si un objeto se mueve con una velocidad v respecto a un sistema de referencia, que a su vez se mueve con una velocidad w respecto a un segundo sistema de referencia, entonces la velocidad del objeto respecto al segundo sistema de referencia será:
W = w + v
Supongamos un rayo de luz en el interior de un tren. Respecto al tren la velocidad de la luz sería:
w= c-v
cuando respecto a las vías sería c.
Pero el principio de relatividad dice que las leyes deben ser las mismas para dos sistemas de referencia con movimiento relativo unifirme ¿Qué es incorrecto? Nada de esto. Lo incorrecto son nuestras nociones de espacio y tiempo.
La Relatividad de la Simultaneidad
Para saber si dos sucesos son simultáneos necesitamos una definición que nos proporcione un método para comprobarlo empíricamente.
De la definición de simultaneidad llegamos a una definición de tiempo como aquel marcado por un reloj contiguo al suceso en el espacio y en reposo respecto a él. Dos relojes marcan el mismo tiempo si la posición de sus manillas son simultáneas una vez calibradas.
Dos sucesos simultáneos en un sistema de referencia no lo son para otro sistema de referencia en movimiento relativo. Existe la relatividad de la simultaneidad. Cada cuerpo de referencia tiene su tiempo especial con lo que una localización temporal tiene sentido solo si se indica el sistema de referencia al que se refiere. Por tanto el tiempo absoluto es incompatible con la definición de simultaneidad.
Si prescindimos del tiempo absoluto desaparece el conflicto entre el principio de relatividad y la ley de propagación de la luz. Además deja de ser válido el teorema de adición de velocidades de la mecánica clásica comentado anteriormente.
La Relatividad de la Distancia Espacial
La Relatividad de la Distancia Espacial
Para medir una distancia se necesita un cuerpo de referencia respecto al cual hacerlo. Si el objeto a medir está en reposo respecto al sistema de referencia, entonces la medición puede hacerse transportando una regla rígida desde el punto origen hasta el punto destino.
Pero si queremos medir distancias en un cuerpo en movimiento respecto al sistema de referencia, debemos utilizar la definición de tiempo mostrada anteriormente. Debemos medir con nuestro reloj los instantes en que los puntos origen y destino del objeto en movimiento pasan junto a nosotros, restarlos y multiplicar el intervalo obtenido por la velocidad del cuerpo.
Por tanto, la aparente incompatibilidad entre la ley de propagación de la luz y el principio de relatividad está basada en dos hipótesis injustificadas:
- El intervalo temporal entre dos sucesos es independiente del estado de movimiento del cuerpo de referencia.
- El intervalo espacial entre dos puntos de un cuerpo rígido es independiente del estado de movimiento del cuerpo de referencia.
Sin estas hipótesis surge la posibilidad de que la ley de propagación de la luz sea compatible con el principio de relatividad.
Las Transformaciones de Lorentz
Las Transformaciones de Lorentz
¿Cómo se hallan el lugar y el tiempo de un suceso con relación a un sistema de coordenadas cuando se conocen el lugar y el tiempo del suceso con respecto a otro? ¿Esta pregunta tiene alguna respuesta de acuerdo con la cual la ley de propagación de la luz no contradiga el principio de relatividad? O dicho de otra manera: ¿Existe alguna relación entre las posiciones y los tiempos de los distintos sucesos con relación a ambos sistemas de referencia, de manera que todo rayo de luz tenga la velocidad de propagación c respecto a ambos sistemas?
La respuesta es afirmativa: las transformaciones de Lorentz.
Transformaciones de Lorentz
Si la velocidad de la luz tiende a infinito, las transformaciones de Lorentz se reducen a las transformaciones de Galileo.
Por ejemplo, para un rayo de luz se cumple que si su velocidad es c para un sistema de coordenadas, también lo es para otro en movimiento rectilíneo uniforme. Partiendo de x=ct, sustituyendo x y t en las expresiones de x' y t' de las transformaciones de Lorentz y dividiendo x' entre t' se obtiene que x'=ct'.
El Comportamiento de reglas y relojes en movimiento
A partir de las transformaciones de Lorentz, se obtiene la contracción de longitudes para reglas en movimiento:
Δx' = Δx · γ
Además, las transformaciones de Lorentz muestran que el tiempo pasa más lento para relojes en movimiento:
Siendo γ en ambos casos:
Δt' = Δt · γ
Siendo γ en ambos casos:
Por tanto la velocidad de la luz es un límite que no puede ser superado porque entonces las longitudes y los tiempos serían imaginarios, lo que no es válido físicamente.
De acuerdo con el principio de relatividad, cada observador en movimiento relativo ve las reglas del otro más cortas y su tiempo pasa más despacio. Distancias más cortas y tiempos más lentos hacen que los efectos se cancelen y que la velocidad de la luz siga siendo constante e igual a c para cada observador.
El Teorema de Adición de Velocidades
El Teorema de Adición de Velocidades
A partir de las transformaciones de Lorentz se puede llegar a un teorema de adición de velocidades compatible con el principio de relatividad y la ley de propagación de la luz:
Si el producto vw es mucho menor que c², entonces obtenemos la adición de velocidades clásica W = v + w.
Si v=w=c, entonces obtenemos W=c. Nunca se puede obtener, por tanto, una velocidad superior a la de la luz.
Resumiendo las Ideas Clave de la Relatividad Especial
La Teoría de la Relatividad surge de la electrodinámica como resumen y generalización asombrosamente sencillos de las hipótesis, antes mutuamente independientes, que servían de fundamento a la electrodinámica.
Teorema de adición de velocidades según la Teoría de la Relatividad Especial
Si el producto vw es mucho menor que c², entonces obtenemos la adición de velocidades clásica W = v + w.
Si v=w=c, entonces obtenemos W=c. Nunca se puede obtener, por tanto, una velocidad superior a la de la luz.
Resumiendo las Ideas Clave de la Relatividad Especial
La Teoría de la Relatividad surge de la electrodinámica como resumen y generalización asombrosamente sencillos de las hipótesis, antes mutuamente independientes, que servían de fundamento a la electrodinámica.
Uniendo la transformación de Lorentz con el Principio de Relatividad podemos resumir la Teoría de la Relatividad como:
Toda ley general de la naturaleza tiene que estar constituida de tal forma que se transforme en otra ley de idéntica estructura al introducir, en lugar de las variables espacio-temporales x, y, z, t del sistema de coordenadas original K, nuevas variables espacio-temporales x', y', z', t' de otro sistema de coordenadas K', donde la relación entre las cantidades con prima y sin prima viene dada por la transformación de Lorentz.
Formulado brevemente: las leyes generales de la naturaleza son covariantes respecto a la transformación de Lorentz. Esto constituye una nueva simetría espacio-temporal de la naturaleza.
Esta simetría concreta que la Relatividad impone a las leyes naturales se convierte en valioso auxiliar heurístico en la búsqueda de leyes generales de la naturaleza.
Resultados Generales de la Teoría
Uno de los éxitos de La Relatividad Especial es el haber simplificado mucho el edificio teórico de la electrodinámica y la óptica, reduciendo mucho el número de hipótesis independientes sobre las que descansan.
Además, de esta teoría se obtiene una nueva definición de energía total E y de energía cinética K:
E = γm0c2 = K + m0c2 = mc2
donde m0 es la masa en reposo del cuerpo y m su masa inercial. Desarrollando en serie de potencias E = γm0c2 se obtiene:
En esta imagen m se corresponde con m0 en la fórmula anterior. Al desarrollar E = γm0c2 en serie de potencias se obtiene, para un valor de v mucho menor que c, la definición clásica de energía cinética ½mv²
Por tanto la energía total es:
E = γm0c2 ~ m0c2 + ½m0v²
Sin embargo, el resultado más importante concierne al concepto de masa. Antes de la teoría existian dos principios de conservación independientes: el de la masa y el de la energía. La Teoría de la Relatividad los funde en uno solo.
Si un cuerpo absorbe una cierta energía, su masa inercial crece con lo que esta no es constante, sino variable según la modificación de su energía. Es decir, la masa inercial de un cuerpo es una medida de su energía.
Hasta principios del S. XX se podía establecer el principio de conservación de la masa porque hace falta muchísima energía para variar la masa de un cuerpo.
Además la Teoría de la Relatividad confirma el uso del concepto de campo, usado por primera vez por Faraday y Maxwell, con velocidad de propagación finita en lugar de la acción a distancia instantánea de la Ley de Gravitación de Newton.
En la Teoría de la Relatividad siempre hay una acción a distancia con velocidad de propagación finita, que coincide con la de la luz debido al papel teórico que desempeña la velocidad c en esta teoría.
La equivalencia entre masa y energía permite fusionar los principios de conservación de la masa y la energía en uno solo: el de la masa-energía
Si un cuerpo absorbe una cierta energía, su masa inercial crece con lo que esta no es constante, sino variable según la modificación de su energía. Es decir, la masa inercial de un cuerpo es una medida de su energía.
Hasta principios del S. XX se podía establecer el principio de conservación de la masa porque hace falta muchísima energía para variar la masa de un cuerpo.
Además la Teoría de la Relatividad confirma el uso del concepto de campo, usado por primera vez por Faraday y Maxwell, con velocidad de propagación finita en lugar de la acción a distancia instantánea de la Ley de Gravitación de Newton.
En la Teoría de la Relatividad siempre hay una acción a distancia con velocidad de propagación finita, que coincide con la de la luz debido al papel teórico que desempeña la velocidad c en esta teoría.
La Teoría de la Relatividad Especial y la Experiencia
La Teoría de la Relatividad Especial está apoyada por muchas evidencias experimentales, entre las que se pueden destacar:
En general, como la teoría de la Relatividad cristalizó a partir de la Teoría Electromagnética de Maxwell, todos los hechos experimentales que apoyan esta última, también apoyan la teoría relativista. Pueden destacarse:
Las transformaciones de Lorentz fueron derivadas para intentar justificar las complicadas leyes que surgían de aplicar las transformaciones de Galileo a las Leyes de Maxwell. Daban un resultado correcto, pero con unas explicaciones teóricas rebuscadas y difícilmente creíbles.
Espacio-tiempo Cuadridimensional de Minkowski
El hecho de que el tiempo ya no sea absoluto y esté interrelacionado con las coordenadas espaciales mediante las transformaciones de Lorentz hace natural la unificación del espacio y el tiempo en un único ente: el espacio-tiempo de 4 dimensiones.
Además de unificar los principios de conservación independientes de la masa y la energía en un solo, la Teoría de la Relatividad realiza otra unificación: la del espacio y el tiempo en el espacio-tiempo.
En el espacio-tiempo de Minkowski los problemas de la Teoría de la Relatividad pueden resolverse de manera geométrica. Esta es una de sus grandes ventajas.
Del análisis teórico del principio de relatividad general puede extraerse alguna conclusión de las características que debe tener el campo gravitatorio. Por ejemplo, los rayos de luz en el seno de un campo gravitatorio se propagan, en general, según líneas curvas.
Ejemplo del Disco Giratorio
Se puede interpretar la fuerza centrífuga en el ejemplo de un disco en rotación como la acción de un campo gravitatorio. Si colocamos un reloj en el centro y otro en un extremo, este segundo reloj tendrá una velocidad respecto al primero, con lo que según la Teoría de la Relatividad Especial no marcarán el mismo tiempo. Concretamente el reloj en el extremo irá más despacio.
Por tanto, podemos pensar que en general los relojes en el seno de un campo gravitatorio no marcaran el mismo tiempo en función del lugar en el que se encuentren.
Igualmente, si un observador en el extremo del disco coloca tangencialmente una regla de longitud 1 en reposo respecto a él, esta regla medirá menos de 1 para el observador en el centro del disco. Si la coloca radialmente, la regla entonces no se acorta. Si el observador en el centro del disco calcula entonces la relación entre el perímetro y el diámetro no obtendrá el valor π, con lo que la geometría euclídea deja de ser válida.
Por tanto, para generalizar el principio de relatividad no podemos seguir basándonos, a diferencia de la Relatividad Especial, en la geometría euclidiana y debemos abandonar las coordenadas cartesianas, pues son exclusivas de esta geometría. Y mientras las coordenadas y los tiempos de los sucesos no estén definidos, tampoco tienen significado exacto las leyes de la naturaleza en las que aparecen esas coordenadas.
La generalización de la geometría euclidiana fue realizada por Gauss y Riemann. Los espacios de Riemann son contínuos curvos en los que localmente, o infinitesimalmente, es válida la geometría euclidiana, y son exactamente los necesarios para modelar la nueva geometría del espacio-tiempo que surge del principio de relatividad generalizado.
En el caso del disco giratorio, la geometría viene determinada por la métrica:
Esta métrica es fruto de una transformación de coordenadas respecto de un espacio-tiempo de Minkowski:
ds2 = (cdt)2 - (dr)2 - r²(dθ)² (espacio-tiempo de Minkowski en coordenadas polares)
ds2 = (cdt)2 - (dx)2 - (dy)2 (espacio-tiempo de Minkowski en coordenadas cartesianas)
Si ω es igual a 0, resulta el espacio-tiempo plano de la Relatividad Especial en coordenadas polares. Es lógico pues el disco ya no gira.
Si dt=0, entonces la distancia ds² es la de un plano en coordenadas polares. Este caso es como si congeláramos el movimiento del disco.
El tiempo propio para un observador en el centro y en el extremo del disco es:
Donde se ha tenido en cuenta que v = rω.
Por tanto, como γ es mayor que 1, para un observador girando sobre el disco el tiempo pasará más despacio cuanto más alejado del centro esté.
Para un observador en el centro del disco, r=0 o γ = 1, el tiempo transcurre igual que para un observador externo. Esto es porque debido a la simetría de giro, el centro del disco gira pero no se desplaza.
Para un observador girando a una cierta distancia del centro el espacio ya no es euclidiano. Considerando que las distancias varían en la dirección del movimiento (tangencial) pero no en la perpendicular al movimiento (radial), un observador en el extremo del disco medirá un perímetro mayor pero un mismo radio. Así obtendrá un valor mayor que π para el cociente entre la longitud de la circunferencia y del diámetro del disco. Realmente medirá el valor πγ.
El término cruzado 2r²ωdtdθ nos dice que las variables t y θ no son independientes. De hecho, al girar el disco el ángulo depende del tiempo. Por ello no es posible encontrar una parametrización en que t y θ sean ortogonales.
Si en lugar de un disco giratorio tuviéramos un disco que no rota pero que se expande y contrae cíclicamente, entonces aparecería un término dtdr en lugar de dtdθ.
Este espacio no es isótropo porque, al girar el disco, existe una dirección privilegiada, la de la dirección del eje de rotación. Esto se aprecia en la métrica por la existencia del término dtdθ.
Principio de Relatividad Generalizado
Según la Teoría de la Relatividad Especial gozan de privilegio ciertos sistemas de coordenadas: los sistemas de referencia de Galileo. Para el paso de un sistema de Galileo a otro que se mueva uniformemente respecto al primero son válidas las transformaciones de Lorentz.
Estas ecuaciones constituyen la base para derivar las consecuencias de la Teoría de la Relatividad Especial y no son más que la expresión de la validez universal de la ley de propagación de la luz para todos los sistemas de referencia de Galileo.
Minkowski descubrió que las transformaciones de Lorentz mantienen invariante la distancia entre dos sucesos en el espacio-tiempo cuadridimensional. Es decir, la distancia tiene el mismo valor para todos los cuerpos de referencia privilegiados (los de Galileo), con lo que es independiente de la elección del sistema de referencia. Esta distancia al cuadrado es:
Según la teoría de la Relatividad Especial, al hacer una transformación de coordenadas utilizando la transformación de Lorentz, las ecuaciones de las leyes de la naturaleza se convierten en otras de la misma forma. En el caso de la Teoría de la Relatividad General debemos aspirar a lo mismo pero en el entorno de los espacios de Riemann y para todas las transformaciones de coordenadas posibles.
En el caso de la Relatividad Especial siempre nos referimos a sistemas de referencia de Galileo, es decir, aquellos en los que no existe ningún campo gravitatorio. Si referimos esas mismas regiones de Galileo a cuerpos de referencia no galileanos, entonces respecto a estos últimos aparece un campo gravitatorio de tipo especial.
Sin embargo, en los campos gravitatorios no existen cuerpos rígidos con propiedades euclidianas para ser utilizados como sistemas de referencia respecto a los que medir distancias. Y los campos gravitatorios también influyen en la marcha de los relojes.
Por eso deben usarse cuerpos de referencia no rígidos que además de un movimiento arbitrario también sufren alteraciones en su forma durante dicho movimiento.
Para la definición de tiempo sirven relojes cuya marcha responda a una ley arbitraria. Solo es necesario que se cumpla una condición: que los tiempos entre relojes cercanos difieran infinitamente poco entre sí.
El principio de relatividad general exige que los sistemas de referencia sean equivalentes y en todos ellos sean válidas las leyes de la naturaleza. Estas leyes deben ser totalmente independientes de la elección del sistema de referencia.
La importancia adicional del principio de relatividad general es que impone profundas restricciones a las leyes de la naturaleza.
El principio de relatividad general nos permite por fin determinar la influencia del campo gravitatorio sobre la evolución de todos aquellos procesos que en ausencia de campo gravitatorio discurren según leyes conocidas, es decir, que están incluidos ya en el marco de la Relatividad Especial.
La Posibilidad de un Universo Finito no limitado
A pequeña escala podría ser que un espacio fuera cuasi euclidiano y aún así ser curvo en global, como en el caso de una superficie esférica, que es localmente casi plana pero curva en su globalidad.
Según la Teoría de la Relatividad General, las propiedades geométricas del espacio no son independientes, sino que vienen condicionadas por la materia. Por eso no es posible inferir nada sobre la estructura geométrica del mundo a menos que la reflexión se funde en el conocimiento del estado de la materia.
Si suponemos que la materia está en reposo (o que se mueve lentamente respecto a la velocidad de la luz), podremos conocer la estructura del Universo en una primera aproximación.
Sabemos que las distancias y los tiempos son afectados por los campos gravitatorios, es decir, por la distribución de materia. Por tanto, la geometría euclidiana no es válida en nuestro mundo. Sin embargo, las distribuciones de materia habituales curvan poco el espacio-tiempo, pudiéndolo considerar como casi plano o cuasi-euclidiano. Pero en un espacio cuasi-euclidiano la densidad media de materia tendría que ser nula.
Si la densidad de materia no es nula, aunque sea muy pequeña, y uniforme, el mundo no es cuasi-euclidiano, sino esférico. Considerando que localmente la materia no está distribuida de manera uniforme, el mundo será cuasi-esferico a nivel local pero esférico a nivel global, y por tanto, finito y sin límites de manera similar a una esfera.
La Teoría de la Relatividad Especial está apoyada por muchas evidencias experimentales, entre las que se pueden destacar:
- La ley de composición de velocidades confirmada por el experimento de Fizeau.
- El efecto Doppler relativista confirmado por el grado de corrimiento hacia el rojo de las líneas espectrales de la luz de las estrellas.
En general, como la teoría de la Relatividad cristalizó a partir de la Teoría Electromagnética de Maxwell, todos los hechos experimentales que apoyan esta última, también apoyan la teoría relativista. Pueden destacarse:
- Las Leyes de Maxwell no son covariantes bajo las transformaciones de Galileo de la mecánica clásica y sí bajo las transformaciones de Lorentz.
- La ley de movimiento de los electrones en las emisiones radiactivas beta predicha correctamente por la Teoría de la Relatividad.
- El experimento de Michelson-Morley que descarta la existencia del éter luminífero postulado para intentar explicar la existencia de un sistema de referencia privilegiado que justificara la validez de las ecuaciones de Maxwell en un sistema de referencia pero no en otros al aplicar las transformaciones de Galileo.
Las transformaciones de Lorentz fueron derivadas para intentar justificar las complicadas leyes que surgían de aplicar las transformaciones de Galileo a las Leyes de Maxwell. Daban un resultado correcto, pero con unas explicaciones teóricas rebuscadas y difícilmente creíbles.
Espacio-tiempo Cuadridimensional de Minkowski
El hecho de que el tiempo ya no sea absoluto y esté interrelacionado con las coordenadas espaciales mediante las transformaciones de Lorentz hace natural la unificación del espacio y el tiempo en un único ente: el espacio-tiempo de 4 dimensiones.
Espacio-tiempo de Minkowski de 2 dimensiones: una espacial y una temporal. En negro se dibuja un sistema de coordenadas y en azul, otro con velocidad relativa v. E es un evento referido a las coordenadas de ambos sistemas
Además de unificar los principios de conservación independientes de la masa y la energía en un solo, la Teoría de la Relatividad realiza otra unificación: la del espacio y el tiempo en el espacio-tiempo.
En el espacio-tiempo de Minkowski los problemas de la Teoría de la Relatividad pueden resolverse de manera geométrica. Esta es una de sus grandes ventajas.
Segunda Parte
Sobre la Teoría de la Relatividad General
Hasta ahora hemos visto que se puede aplicar exitosamente el Principio de Relatividad a todos aquellos sistemas de referencia con movimiento relativo rectilíneo, uniforme e irrotacional.
Pero ¿Qué sucede con el resto de sistemas de referencia con movimiento relativo diferente?¿Son los sistemas de referencia de Galileo privilegiados respecto al resto? La respuesta es que no. Pero para ello el Principio de Relatividad debe ser generalizado.
El Campo Gravitatorio
De manera similar al electromagnetismo, los cuerpos ejercen la atracción gravitatoria mediante la generación de un campo, en este caso el gravitatorio. Es decir, no hay acción a distancia instantánea como presupone la Ley de Newton.
Sin embargo, a diferencia del campo electromagnético, los cuerpos que se mueven bajo la acción de un campo gravitatorio experimentan una aceleración que no depende del material del cuerpo ni de su estado de movimiento. Esto es equivalente a afirmar que la masa inercial de un cuerpo es igual a la masa gravitatoria. Un cuerpo manifiesta una u otra masa en función de la situación.
Podemos seguir considerando un sistema de referencia en movimiento acelerado uniforme respecto a uno de Galileo como también de Galileo si consideramos la existencia de un campo gravitatorio uniforme.
Por tanto la existencia de un campo gravitatorio nos permite generalizar el principio de relatividad a todos los sistemas de referencia a cambio de tener que encontrar unas leyes que describan el campo gravitatorio que aparece en el sistema de referencia con movimiento acelerado.
La generalización del principio de relatividad es posible gracias al postulado de igualdad entre masa inercial y masa gravitatoria.
No siempre se puede afirmar que el movimiento es indistinguible de la acción de un campo gravitatorio. Es decir, que el campo gravitatorio es aparente y puede eliminarse mediante una transformación de coordenadas apropiada. Solo en casos especiales de campos gravitatorios uniformes. El de la tierra no, por ejemplo.
La generalización del principio de relatividad y las nuevas leyes de transformación de coordenadas proporcionarán las leyes del campo gravitatorio, pues este aparece como consecuencia del movimiento acelerado del sistema de referencia.
La consideración de una fuerza, la fuerza gravitatoria, permite unificar todos los sistemas de referencia y unificar el movimiento uniforme con el movimiento acelerado. Es una nueva simetría escondida de la naturaleza que emerge al considerar una nueva fuerza. O, dicho de otra manera, la gravedad existe para que se conserve la simetría entre los sistemas de referencia.
Del análisis teórico del principio de relatividad general puede extraerse alguna conclusión de las características que debe tener el campo gravitatorio. Por ejemplo, los rayos de luz en el seno de un campo gravitatorio se propagan, en general, según líneas curvas.
Ejemplo del Disco Giratorio
Se puede interpretar la fuerza centrífuga en el ejemplo de un disco en rotación como la acción de un campo gravitatorio. Si colocamos un reloj en el centro y otro en un extremo, este segundo reloj tendrá una velocidad respecto al primero, con lo que según la Teoría de la Relatividad Especial no marcarán el mismo tiempo. Concretamente el reloj en el extremo irá más despacio.
Por tanto, podemos pensar que en general los relojes en el seno de un campo gravitatorio no marcaran el mismo tiempo en función del lugar en el que se encuentren.
Igualmente, si un observador en el extremo del disco coloca tangencialmente una regla de longitud 1 en reposo respecto a él, esta regla medirá menos de 1 para el observador en el centro del disco. Si la coloca radialmente, la regla entonces no se acorta. Si el observador en el centro del disco calcula entonces la relación entre el perímetro y el diámetro no obtendrá el valor π, con lo que la geometría euclídea deja de ser válida.
Por tanto, para generalizar el principio de relatividad no podemos seguir basándonos, a diferencia de la Relatividad Especial, en la geometría euclidiana y debemos abandonar las coordenadas cartesianas, pues son exclusivas de esta geometría. Y mientras las coordenadas y los tiempos de los sucesos no estén definidos, tampoco tienen significado exacto las leyes de la naturaleza en las que aparecen esas coordenadas.
La generalización de la geometría euclidiana fue realizada por Gauss y Riemann. Los espacios de Riemann son contínuos curvos en los que localmente, o infinitesimalmente, es válida la geometría euclidiana, y son exactamente los necesarios para modelar la nueva geometría del espacio-tiempo que surge del principio de relatividad generalizado.
En el caso del disco giratorio, la geometría viene determinada por la métrica:
ds² = (c² - r²ω²)dt² - dr² - r²dθ² - 2r²ωdtdθ
ds2 = (cdt)2 - (dr)2 - r²(dθ)² (espacio-tiempo de Minkowski en coordenadas polares)
ds2 = (cdt)2 - (dx)2 - (dy)2 (espacio-tiempo de Minkowski en coordenadas cartesianas)
Si ω es igual a 0, resulta el espacio-tiempo plano de la Relatividad Especial en coordenadas polares. Es lógico pues el disco ya no gira.
Si dt=0, entonces la distancia ds² es la de un plano en coordenadas polares. Este caso es como si congeláramos el movimiento del disco.
El tiempo propio para un observador en el centro y en el extremo del disco es:
dτ² = (c² - r²ω²)dt²/c² = dt²/γ²
Con lo que el tiempo propio resulta:
τ = t/γ
Donde se ha tenido en cuenta que v = rω.
Por tanto, como γ es mayor que 1, para un observador girando sobre el disco el tiempo pasará más despacio cuanto más alejado del centro esté.
Para un observador en el centro del disco, r=0 o γ = 1, el tiempo transcurre igual que para un observador externo. Esto es porque debido a la simetría de giro, el centro del disco gira pero no se desplaza.
Para un observador girando a una cierta distancia del centro el espacio ya no es euclidiano. Considerando que las distancias varían en la dirección del movimiento (tangencial) pero no en la perpendicular al movimiento (radial), un observador en el extremo del disco medirá un perímetro mayor pero un mismo radio. Así obtendrá un valor mayor que π para el cociente entre la longitud de la circunferencia y del diámetro del disco. Realmente medirá el valor πγ.
El término cruzado 2r²ωdtdθ nos dice que las variables t y θ no son independientes. De hecho, al girar el disco el ángulo depende del tiempo. Por ello no es posible encontrar una parametrización en que t y θ sean ortogonales.
Si en lugar de un disco giratorio tuviéramos un disco que no rota pero que se expande y contrae cíclicamente, entonces aparecería un término dtdr en lugar de dtdθ.
Este espacio no es isótropo porque, al girar el disco, existe una dirección privilegiada, la de la dirección del eje de rotación. Esto se aprecia en la métrica por la existencia del término dtdθ.
Principio de Relatividad Generalizado
Según la Teoría de la Relatividad Especial gozan de privilegio ciertos sistemas de coordenadas: los sistemas de referencia de Galileo. Para el paso de un sistema de Galileo a otro que se mueva uniformemente respecto al primero son válidas las transformaciones de Lorentz.
Estas ecuaciones constituyen la base para derivar las consecuencias de la Teoría de la Relatividad Especial y no son más que la expresión de la validez universal de la ley de propagación de la luz para todos los sistemas de referencia de Galileo.
Minkowski descubrió que las transformaciones de Lorentz mantienen invariante la distancia entre dos sucesos en el espacio-tiempo cuadridimensional. Es decir, la distancia tiene el mismo valor para todos los cuerpos de referencia privilegiados (los de Galileo), con lo que es independiente de la elección del sistema de referencia. Esta distancia al cuadrado es:
ds2 = (cdt)2 - (dx)2 - (dy)2 - (dz)2
Según la teoría de la Relatividad Especial, al hacer una transformación de coordenadas utilizando la transformación de Lorentz, las ecuaciones de las leyes de la naturaleza se convierten en otras de la misma forma. En el caso de la Teoría de la Relatividad General debemos aspirar a lo mismo pero en el entorno de los espacios de Riemann y para todas las transformaciones de coordenadas posibles.
En el caso de la Relatividad Especial siempre nos referimos a sistemas de referencia de Galileo, es decir, aquellos en los que no existe ningún campo gravitatorio. Si referimos esas mismas regiones de Galileo a cuerpos de referencia no galileanos, entonces respecto a estos últimos aparece un campo gravitatorio de tipo especial.
Sin embargo, en los campos gravitatorios no existen cuerpos rígidos con propiedades euclidianas para ser utilizados como sistemas de referencia respecto a los que medir distancias. Y los campos gravitatorios también influyen en la marcha de los relojes.
Por eso deben usarse cuerpos de referencia no rígidos que además de un movimiento arbitrario también sufren alteraciones en su forma durante dicho movimiento.
Para la definición de tiempo sirven relojes cuya marcha responda a una ley arbitraria. Solo es necesario que se cumpla una condición: que los tiempos entre relojes cercanos difieran infinitamente poco entre sí.
El principio de relatividad general exige que los sistemas de referencia sean equivalentes y en todos ellos sean válidas las leyes de la naturaleza. Estas leyes deben ser totalmente independientes de la elección del sistema de referencia.
La importancia adicional del principio de relatividad general es que impone profundas restricciones a las leyes de la naturaleza.
La Solución del Problema de la Gravitación sobre la base del Principio de la Relatividad General
En ausencia de campos gravitatorios el comportamiento de reglas y relojes respecto a un sistema de referencia de Galileo es conocido mediante la Relatividad Especial.
Si referimos esta región a un cuerpo de referencia arbitrario entonces respecto a este cuerpo de referencia existe un campo gravitatorio (de clase especial).
Por transformación de coordenadas se obtiene el comportamiento de reglas y relojes así como de puntos materiales libremente móviles respecto a este sistema de referencia arbitrario. Este comportamiento se interpreta como un comportamiento bajo la acción de un campo gravitatorio.
Se introduce entonces la hipótesis de que la acción del campo gravitatorio se produce según las mismas leyes aún en el caso de que el campo gravitatorio reinante no se pueda derivar del caso especial galileano por mera transformación de coordenadas.
A continuación se investiga el comportamiento espacio-temporal del campo gravitatorio derivado del caso especial galileano por simple transformación de coordenadas y se formula este comportamiento mediante una ley que sea válida independientemente del sistema de referencia escogido.
Esta ley no es todavía la ley general del campo gravitatorio, porque este campo gravitatorio es de una clase especial. Para hallar la ley general del campo gravitatorio hace falta generalizar además la ley así obtenida. Puede encontrarse esta ley general si se tiene en cuenta:
- La generalización buscada debe satisfacer también el postulado de la Relatividad General.
- Si existe materia en la región considerada, entonces su única fuente es su masa inercial, o equivalentemente, su energía.
- El Campo Gravitatorio y la materia deben satisfacer juntos la ley de conservación de la energía (y del momento lineal).
Ecuaciones de campo de la Relatividad General que proporcionan las gμν que caracterizan la geometría y la métrica el espacio-tiempo creado por una distribución de masa-energía concreta
El principio de relatividad general nos permite por fin determinar la influencia del campo gravitatorio sobre la evolución de todos aquellos procesos que en ausencia de campo gravitatorio discurren según leyes conocidas, es decir, que están incluidos ya en el marco de la Relatividad Especial.
Confirmación de la Relatividad General por la experiencia
En el momento de la aparición de la Teoría de la Relatividad apenas se habían detectado unos pocos resultados experimentales que no fueran explicados por la Ley de Gravitación Universal de Newton.
Esto se debe a que la ley de Newton se obtiene como primera aproximación de la Relatividad General cuando los campos gravitatorios son débiles y las velocidades son pequeñas respecto a la de la luz.
Estos resultados experimentales eran:
- Avance del perihelio de Mercurio. Según la Teoría de la Relatividad General toda elipse planetaria alrededor del Sol debe rotar en el sentido de su revolución.
Avance del perihelio de Mercurio donde a es el radio de la órbita, T el periodo, c la velocidad de la luz y e la excentricidad de la órbita
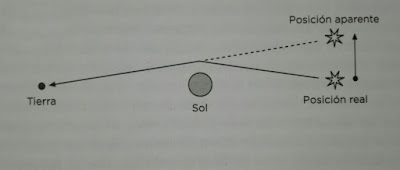
- Curvatura de los Rayos luminosos en el campo gravitatorio del Sol.
Curvatura de los rayos luminosos debido al campo gravitatorio del Sol
- Corrimiento al rojo de las rayas espectrales debido al potencial gravitatorio de las grandes estrellas respecto a la luz generada de manera equivalente en la Tierra.
Corrimiento al rojo de las rayas espectrales debido al potencial gravitatorio
Potencial gravitatorio de una estrella según la Ley de Gravitación de Newton
Cosmología
Lo mas sencillo es pensar que nuestro Universo es infinito espacial y temporalmente. Sin embargo esto es incompatible con la teoría de Newton.
La Ley de Gravitación de Newton también es insatisfactoria en cosmología porque predice campos gravitatorios infinitos con densidades de materia medias diferentes de cero. Impide un universo estático porque la gravedad es siempre atractiva, con lo que las estrellas deberían aglutinarse todas en un punto.
Además está la paradoja de Olbers, que afirma que un Universo estático, infinito y eterno implica un cielo brillante porque cada línea de visión coincidiría con una estrella. La solución a esta paradoja es un universo finito o que las estrellas se encendieran en un instante finito del pasado y su luz entonces aún no nos ha llegado.
Posteriormente se descubrió que es imposible un modelo estático e infinito del Universo con la presencia de la gravedad. Solo sería posible con un Universo infinito y la materia distribuida de manera totalmente uniforme. Aún así el equilibrio sería inestable, y cualquier perturbación haría que el Universo se contrayera.
La Ley de Gravitación de Newton también es insatisfactoria en cosmología porque predice campos gravitatorios infinitos con densidades de materia medias diferentes de cero. Impide un universo estático porque la gravedad es siempre atractiva, con lo que las estrellas deberían aglutinarse todas en un punto.
Además está la paradoja de Olbers, que afirma que un Universo estático, infinito y eterno implica un cielo brillante porque cada línea de visión coincidiría con una estrella. La solución a esta paradoja es un universo finito o que las estrellas se encendieran en un instante finito del pasado y su luz entonces aún no nos ha llegado.
Posteriormente se descubrió que es imposible un modelo estático e infinito del Universo con la presencia de la gravedad. Solo sería posible con un Universo infinito y la materia distribuida de manera totalmente uniforme. Aún así el equilibrio sería inestable, y cualquier perturbación haría que el Universo se contrayera.
Einstein creía que el Universo tenía que ser estático aunque sus ecuaciones predecían que lo más probable es que se expandiera o contrayera. Por eso introdujo la Constante Cosmológica, que era como una gravedad repulsiva para compensar el efecto atractivo de la gravedad.
La Posibilidad de un Universo Finito no limitado
A pequeña escala podría ser que un espacio fuera cuasi euclidiano y aún así ser curvo en global, como en el caso de una superficie esférica, que es localmente casi plana pero curva en su globalidad.
Según la Teoría de la Relatividad General, las propiedades geométricas del espacio no son independientes, sino que vienen condicionadas por la materia. Por eso no es posible inferir nada sobre la estructura geométrica del mundo a menos que la reflexión se funde en el conocimiento del estado de la materia.
Si suponemos que la materia está en reposo (o que se mueve lentamente respecto a la velocidad de la luz), podremos conocer la estructura del Universo en una primera aproximación.
Sabemos que las distancias y los tiempos son afectados por los campos gravitatorios, es decir, por la distribución de materia. Por tanto, la geometría euclidiana no es válida en nuestro mundo. Sin embargo, las distribuciones de materia habituales curvan poco el espacio-tiempo, pudiéndolo considerar como casi plano o cuasi-euclidiano. Pero en un espacio cuasi-euclidiano la densidad media de materia tendría que ser nula.
Si la densidad de materia no es nula, aunque sea muy pequeña, y uniforme, el mundo no es cuasi-euclidiano, sino esférico. Considerando que localmente la materia no está distribuida de manera uniforme, el mundo será cuasi-esferico a nivel local pero esférico a nivel global, y por tanto, finito y sin límites de manera similar a una esfera.
El Problema del Espacio
La Teoría de Newton presupone un espacio y un tiempo absolutos con existencia real independiente de los cuerpos que en ellos se mueven.
Un espacio independiente es necesario para definir el concepto de aceleración, crucial en la teoría newtoniana, pues la aceleración es respecto al espacio. Análogamente ocurre con el tiempo, pues este también entra en el concepto de aceleración.
Sin embargo en la Teoría de la Relatividad General no existe el concepto de aceleración, pues los objetos se mueven siguiendo trayectorias de aceleración nula (geodésicas) en el espacio-tiempo curvado por la presencia de masa-energía.
¿Qué pasa con la geometría si el tamaño de los objetos es variable en función de las coordenadas? (por ejemplo por dilatación en un campo de temperatura). La geometría debe adaptarse a la realidad física, a los objetos corpóreos. El concepto de objeto corpóreo es previo al de espacio y al de tiempo.
El Concepto de Campo
El Concepto de campo permite superar el pensamiento de que en ausencia de materia queda un espacio vacío. Como decía Descartes, no existe espacio sin extensión, sin magnitud física.
Según la mecánica clásica, si desapareciera la materia, quedarían únicamente el espacio y el tiempo (como un escenario del acontecer físico). La superación de este punto de vista fue el resultado de la aparición del concepto de campo y su aspiración final de sustituir el concepto de partícula (punto material).
Faraday y Maxwell introdujeron el concepto de campo en sus leyes para explicar los fenómenos electromagnéticos. En principio donde no había materia no podia haber campo hasta la aparición de las Leyes de Maxwell que predecían la propagación de la onda electromagnética en el vacío.
En la Teoría de la Relatividad Especial se debe renunciar a la idea de interpretar el campo electromagnético como un estado de un sustrato material, como se intentó con el éter. El campo se convierte así en un elemento irreducible de la descripción física, e irreducible en el mismo sentido que el concepto de materia en la teoría newtoniana.
El Concepto de Espacio en la Teoría de la Relatividad Especial
No obstante la Teoría de la Relatividad Especial, igual que la mecánica clásica, presupone el espacio como algo que viene dado de antemano y que lleva una existencia independiente.
Igual que en la mecánica clásica, en la Relatividad Especial las leyes de la naturaleza solo aspiran a ser válidas cuando la descripción espacio-temporal se basa en un sistema inercial. El principio de inercia y el de la constancia de la velocidad de la luz solamente son válidos respecto a un sistema inercial.
También las leyes del campo aspiran a tener sentido y validez respecto a sistemas inerciales únicamente. Por tanto, al igual que en la mecánica clásica, el espacio es, también aquí, una componente independiente de la representacion de lo físicamente real. El espacio (inercial) es lo que queda al suprimir mentalmente la materia y el campo. Esta estructura cuadridimensional se concibe como soporte de la materia y el campo.
Por tanto para la Teoría de la Relatividad Especial también vale el enunciado: "la descripción de los estados físicos presupone el espacio como algo que viene dado de antemano y que lleva una existencia independiente."
El Concepto de Espacio en la Teoría de la Relatividad General
Respecto a un sistema inercial, el principio de equivalencia nos dice que un sistema de referencia uniformemente acelerado es equivalente a uno inercial asumiendo la existencia de un campo gravitatorio homogéneo en este segundo sistema de referencia. Si el principio de equivalencia puede extenderse a cualquier movimiento relativo entre los sistemas de referencia, entonces el sistema inercial pierde su significado objetivo.
Si sobre el principio de equivalencia podemos construir una teoría consistente y acorde con los experimentos, entonces se satisfará el postulado de la igualdad entre masa inercial y masa gravitatoria.
El paso de un sistema de referencia a otro se corresponde con una transformación no lineal de las cuatro coordenadas. Pero, ¿qué transformaciones no lineales deben permitirse? Es decir, ¿cómo debe generalizarse la transformación de Lorentz?
Para empezar, se deben extender a cualquier tipo de transformación continua porque la Relatividad General se basa en la geometría de Riemann, que al ser contínuo permite que dos sistemas de referencia o dos sucesos puedan estar infinitesimalmente cercanos.
Por tanto la Teoría General de la Relatividad implica que las leyes de la naturaleza tienen que ser covariantes respecto a cualquier transformación continua de coordenadas. Esto aún restringe más las posibles leyes naturales que el principio de la Relatividad Especial.
En Relatividad General el concepto de campo es independiente del contenido físico pues puede interpretarse un movimiento acelerado como un campo gravitatorio sin que se plantée la cuestión de la existencia de masas que engendren el campo.
En el caso de un espacio-tiempo de Minkowski, el de la Relatividad Especial, libre de campo sería el caso más sencillo. Este espacio-tiempo métrico se caracteriza por una definición de distancia que se mantiene invariante bajo las transformaciones de Lorentz. En esta distancia, los elementos del tensor métrico son constantes.
ds2 = (cdt)2 - (dx)2 - (dy)2 - (dz)2
o cambiando el nombre de las coordenadas:
ds2 = dx12 - dx22 - dx32 - dx42
donde los gik = ± 1.
Si en el sentido de la Relatividad General se somete ahora este espacio a una transformación de coordenadas arbitraria pero continua, esa cantidad objetivamente significativa se expresa en el nuevo sistema de coordenadas por la relación:
Un espacio independiente es necesario para definir el concepto de aceleración, crucial en la teoría newtoniana, pues la aceleración es respecto al espacio. Análogamente ocurre con el tiempo, pues este también entra en el concepto de aceleración.
Sin embargo en la Teoría de la Relatividad General no existe el concepto de aceleración, pues los objetos se mueven siguiendo trayectorias de aceleración nula (geodésicas) en el espacio-tiempo curvado por la presencia de masa-energía.
¿Qué pasa con la geometría si el tamaño de los objetos es variable en función de las coordenadas? (por ejemplo por dilatación en un campo de temperatura). La geometría debe adaptarse a la realidad física, a los objetos corpóreos. El concepto de objeto corpóreo es previo al de espacio y al de tiempo.
El Concepto de Campo
El Concepto de campo permite superar el pensamiento de que en ausencia de materia queda un espacio vacío. Como decía Descartes, no existe espacio sin extensión, sin magnitud física.
Según la mecánica clásica, si desapareciera la materia, quedarían únicamente el espacio y el tiempo (como un escenario del acontecer físico). La superación de este punto de vista fue el resultado de la aparición del concepto de campo y su aspiración final de sustituir el concepto de partícula (punto material).
Faraday y Maxwell introdujeron el concepto de campo en sus leyes para explicar los fenómenos electromagnéticos. En principio donde no había materia no podia haber campo hasta la aparición de las Leyes de Maxwell que predecían la propagación de la onda electromagnética en el vacío.
Ecuación de Onda Electromagnética
En la Teoría de la Relatividad Especial se debe renunciar a la idea de interpretar el campo electromagnético como un estado de un sustrato material, como se intentó con el éter. El campo se convierte así en un elemento irreducible de la descripción física, e irreducible en el mismo sentido que el concepto de materia en la teoría newtoniana.
El Concepto de Espacio en la Teoría de la Relatividad Especial
No obstante la Teoría de la Relatividad Especial, igual que la mecánica clásica, presupone el espacio como algo que viene dado de antemano y que lleva una existencia independiente.
Igual que en la mecánica clásica, en la Relatividad Especial las leyes de la naturaleza solo aspiran a ser válidas cuando la descripción espacio-temporal se basa en un sistema inercial. El principio de inercia y el de la constancia de la velocidad de la luz solamente son válidos respecto a un sistema inercial.
También las leyes del campo aspiran a tener sentido y validez respecto a sistemas inerciales únicamente. Por tanto, al igual que en la mecánica clásica, el espacio es, también aquí, una componente independiente de la representacion de lo físicamente real. El espacio (inercial) es lo que queda al suprimir mentalmente la materia y el campo. Esta estructura cuadridimensional se concibe como soporte de la materia y el campo.
Por tanto para la Teoría de la Relatividad Especial también vale el enunciado: "la descripción de los estados físicos presupone el espacio como algo que viene dado de antemano y que lleva una existencia independiente."
El Concepto de Espacio en la Teoría de la Relatividad General
Respecto a un sistema inercial, el principio de equivalencia nos dice que un sistema de referencia uniformemente acelerado es equivalente a uno inercial asumiendo la existencia de un campo gravitatorio homogéneo en este segundo sistema de referencia. Si el principio de equivalencia puede extenderse a cualquier movimiento relativo entre los sistemas de referencia, entonces el sistema inercial pierde su significado objetivo.
Si sobre el principio de equivalencia podemos construir una teoría consistente y acorde con los experimentos, entonces se satisfará el postulado de la igualdad entre masa inercial y masa gravitatoria.
El paso de un sistema de referencia a otro se corresponde con una transformación no lineal de las cuatro coordenadas. Pero, ¿qué transformaciones no lineales deben permitirse? Es decir, ¿cómo debe generalizarse la transformación de Lorentz?
Para empezar, se deben extender a cualquier tipo de transformación continua porque la Relatividad General se basa en la geometría de Riemann, que al ser contínuo permite que dos sistemas de referencia o dos sucesos puedan estar infinitesimalmente cercanos.
Por tanto la Teoría General de la Relatividad implica que las leyes de la naturaleza tienen que ser covariantes respecto a cualquier transformación continua de coordenadas. Esto aún restringe más las posibles leyes naturales que el principio de la Relatividad Especial.
En Relatividad General el concepto de campo es independiente del contenido físico pues puede interpretarse un movimiento acelerado como un campo gravitatorio sin que se plantée la cuestión de la existencia de masas que engendren el campo.
En el caso de un espacio-tiempo de Minkowski, el de la Relatividad Especial, libre de campo sería el caso más sencillo. Este espacio-tiempo métrico se caracteriza por una definición de distancia que se mantiene invariante bajo las transformaciones de Lorentz. En esta distancia, los elementos del tensor métrico son constantes.
ds2 = (cdt)2 - (dx)2 - (dy)2 - (dz)2
o cambiando el nombre de las coordenadas:
ds2 = dx12 - dx22 - dx32 - dx42
donde los gik = ± 1.
Expresión general del intervalo relativista o distancia al cuadrado
Ahora las gik ya no son constantes, sino funciones de las coordenadas, y vienen determinadas por la transformación arbitrariamente elegida.
Expresión general de la distancia al cuadrado en un espacio de Riemann de 4 dimensiones en función de las componentes del tensor métrico, las gik
Según el principio de equivalencia, esta ecuación describe un campo gravitacional de tipo especial, siempre que los gik cumplan la condición de Riemann.
Según la mecánica clásica y la Relatividad Especial, el espacio-tiempo tiene una existencia independiente de la materia o el campo, es decir, viene dado desde un principio.
Por el contrario, según la Teoría de la Relatividad General, el espacio no tiene existencia peculiar al margen de "aquello que llena el espacio", de aquello que depende de las coordenadas.
Si suprimimos mentalmente el campo gravitatorio, esto es, las gik, lo que queda no es un espacio como el de Minkowski, sino que no queda absolutamente nada, ni siquiera un espacio topológico. Pues las funciones gik describen no solo el campo, sino al mismo tiempo la estructura y propiedades topológicas del espacio-tiempo.
Un espacio de Minkowski es, en el sentido de la Relatividad General, no un espacio sin campo, sino un caso especial del campo gik para el cual las gik poseen valores que no dependen de las coordenadas. El espacio vacío, es decir, un espacio sin campo no existe.
Parece ciertamente absurdo que no exista el vacío. Sin embargo esto ocurre si solo consideramos lo físicamente real en los cuerpos ponderables. Es la idea de campo como representante de lo real, en combinación con el principio de relatividad general, lo que muestra la esencia de la idea cartesiana: no existe "espacio libre de campo".
Opinión Personal
En este libro no hay apenas fórmulas ni matemáticas. Se centra en los fundamentos, en los pilares conceptuales en que se basa la Teoría de la Relatividad, en mostrar su esencia y su filosofía. Esto es lo mejor del libro, pues lo hace más sencillo, didáctico y prácticamente apto para todo el mundo.
En el caso de la Relatividad General se explica principalmente el origen y la idea física del Principio de Equivalencia. No se detalla por ejemplo cómo se obtuvieron las ecuaciones de campo ni algunas de las soluciones más conocidas, como la de Schwarzschild que dio origen a los agujeros negros o la de Friedmann, que podría considerarse el inicio de la cosmología moderna.
Respecto a las páginas sobre cosmología, el libro es algo obsoleto pues Einstein aún apostaba por un Universo estático. Sin embargo sí que es didáctico los argumentos que utiliza y la explicación de por qué la Teoría de Newton es incompatible con las observaciones cosmológicas actuales.
Finalmente me ha gustado la explicación de cómo la Relatividad General junto con el concepto de campo cambia nuestra concepción del espacio.

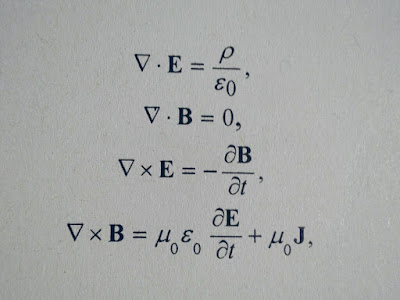
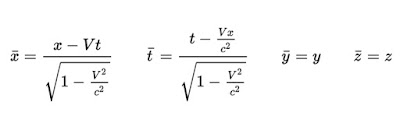










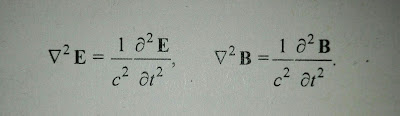


No hay comentarios:
Publicar un comentario