El electromagnetismo de Maxwell es un ejemplo de teoría que unifica y sintetiza. De vez en cuando, con una teoría se obtiene una notable síntesis, comprimiendo en un enunciado breve y elegante muchos fenómenos descritos anteriormente por separado, y en cierta forma, de manera inadecuada.
Un excelente ejemplo procedente de la física fundamental es el trabajo que realizo James Clerck Maxwell entre los años 1850 y 1860 sobre la teoría del electromagnetismo.
Unificación de la electricidad y el magnetismo
En la antigüedad ya se conocían fenómenos electrostáticos simples y familiares, por ejemplo que el ámbar (elektron en griego) tiene la propiedad de atraer pequeños trocitos de plumas cuando se frota con una piel de gato.
Análogamente se conocían algunas propiedades del magnetismo, como el hecho de que el mineral llamado magnetita (un óxido de hierro cuyo nombre deriva de Magnesia, una región de Asia Menor donde era abundante) es capaz de atraer trozos de hierro y magnetizarlos.
Análogamente se conocían algunas propiedades del magnetismo, como el hecho de que el mineral llamado magnetita (un óxido de hierro cuyo nombre deriva de Magnesia, una región de Asia Menor donde era abundante) es capaz de atraer trozos de hierro y magnetizarlos.
En torno al año 1600 electricidad y magnetismo eran considerados dos fenómenos distintos. Hasta el s. XIX no se comprendió la estrechísima relación que hay entre uno y otro.
Los experimentos sobre la corriente eléctrica que siguieron a la invención por Volta de la primera batería eléctrica hacia 1800 abrieron el camino para el descubrimiento de las interacciones entre electricidad y magnetismo.
Hacia 1820 Oersted descubrió que una corriente eléctrica que circula por un cable produce un campo magnético que se enrosca alrededor de este. En 1831 Faraday observó que un campo magnético variable induce una corriente eléctrica en una espiral de alambre. La interpretación posterior de este hecho fue que un campo magnético variable en el tiempo produce un campo eléctrico.
Hacia 1820 Oersted descubrió que una corriente eléctrica que circula por un cable produce un campo magnético que se enrosca alrededor de este. En 1831 Faraday observó que un campo magnético variable induce una corriente eléctrica en una espiral de alambre. La interpretación posterior de este hecho fue que un campo magnético variable en el tiempo produce un campo eléctrico.
En la década de 1850, cuando Maxwell comenzó su trabajo sobre una descripción matemática exhaustiva de los fenómenos electromagnéticos, la mayor parte de las piezas que componían el rompecabezas ya se habían formulado en forma de leyes científicas. El mérito de Maxwell fue enunciar un conjunto de ecuaciones que reproducían dichas leyes.

Ecuaciones de Maxwell en el vacío en forma diferencial. Estas ecuaciones relacionan las causas o fuentes (cargas y corrientes) con los efectos (campos eléctrico y magnético)
En medios materiales como los dieléctricos, las ecuaciones de Maxwell se escriben como:

Ecuaciones de Maxwell en el vacío en forma diferencial. Estas ecuaciones relacionan las causas o fuentes (cargas y corrientes) con los efectos (campos eléctrico y magnético)
En medios materiales como los dieléctricos, las ecuaciones de Maxwell se escriben como:
Ecuaciones de Maxwell en medios materiales donde H es el vector intensidad magnética y D es el vector desplazamiento eléctrico
La relación entre los vectores desplazamiento eléctrico y campo eléctrico, y entre inducción magnética e intensidad magnética es mediante la permitividad eléctrica y permeabilidad magnética respectivamente:
Vectores desplazamiento eléctrico e inducción magnética en función de los campos eléctrico e intensidad magnética
Aunque está implícita en las ecuaciones de Maxwell, también está la ecuación de continuidad o conservación de la carga eléctrica:
Ecuación de continuidad o de conservación de la carga eléctrica
Finalmente hay que añadir la ley de Lorentz que nos dice la fuerza que actúa sobre una carga que se mueve con velocidad v en el seno de un campo electromagnético. Si la carga está en reposo, solo hay contribución del campo eléctrico porque no existe campo magnético (electrostática):
Fuerza de Lorentz
Las Leyes de Maxwell
Primera ley de Maxwell
La primera de las ecuaciones de Maxwell es la ley de Coulomb o ley de Gauss para la electricidad que describe como las cargas eléctricas generan un campo eléctrico.
Segunda ley de Maxwell
Segunda ley de Maxwell
La segunda, conocida como ley de Gauss para el magnetismo, expresa la conjetura de Ampère. Esta conjetura dice que no existen las cargas magnéticas o monopolos magnéticos, de modo que todo el magnetismo se debe a corrientes eléctricas. Esto sitúa al magnetismo en una posición secundaria respecto a la electricidad (en el fondo, una corriente no es más que cargas en movimiento).
Al no existir monopolos magnéticos (eso no quiere decir que no puedan descubrirse en el futuro), es como si hubiera una carga positiva y otra negativa en el mismo punto. Por tanto las líneas de campo magnético no pueden diverger, son curvas y cerradas y todas las que nacen en un dipolo magnético mueren en él. No hay fuentes del campo magnético.
Tercera ley de Maxwell
Tercera ley de Maxwell
La tercera reformula la ley de Faraday, que describe cómo se crea una corriente eléctrica a través de un campo magnético variable.
Cuarta ley de Maxwell
Cuarta ley de Maxwell
La cuarta ecuación, tal y como la formuló Maxwell por primera vez, no era más que la ley de Ampère, que describe como las corrientes eléctricas generan un campo magnético.
Estudiando sus cuatro ecuaciones, Maxwell observó que había algo incorrecto en ellas. Modificando la cuarta ecuación consiguió solucionar el error.
La ley de Ampère solo es correcta para una corriente constante. En el caso que la corriente sea variable con el tiempo (corriente alterna por ejemplo), para que esta ley sea correcta se debe añadir el término introducido por Maxwell y llamado corriente de desplazamiento.
Es decir, la ley de Ampère solamente es aplicable a un conjunto de casos particulares, dado que para que sea válida en todo momento, debería ser siempre nula la divergencia de la corriente, lo cual no es cierto (pues la divergencia del rotacional de H de por si es nula en todos los casos). De hecho, la ley de Ampère solo es válida si la variación temporal de la densidad de carga es nula.
Es decir, la ley de Ampère solamente es aplicable a un conjunto de casos particulares, dado que para que sea válida en todo momento, debería ser siempre nula la divergencia de la corriente, lo cual no es cierto (pues la divergencia del rotacional de H de por si es nula en todos los casos). De hecho, la ley de Ampère solo es válida si la variación temporal de la densidad de carga es nula.
La conservación de la carga eléctrica total es una idea simple y elegante, que confirmada experimentalmente ya era uno de los principios básicos de la física de la época de Maxwell. Sin embargo, sus ecuaciones originales no respetaban este principio.
Examinando la tercera ecuación, se observa un término que describe la generación de un campo eléctrico por un campo magnético variable. ¿Por qué no debería tener la cuarta ecuación un término análogo que describiese la generación de un campo magnético por un campo eléctrico variable?
La hipótesis de Maxwell fue que al segundo miembro de la ley de Ampère había que agregarle un término con dimensiones de densidad de corriente y tal que cumpliera que la divergencia de la densidad de corriente total fuera nula. Por tanto, la divergencia del nuevo miembro debía ser igual a la variación temporal de la densidad de carga eléctrica.
En efecto, con la constante apropiada, el nuevo término añadido a la cuarta ecuación era consistente con el principio de conservación de la carga eléctrica. Es más, esta constante era lo suficientemente pequeña como para que Maxwell pudiese insertar el nuevo término sin introducir resultados que fueran contradictorios con cualquiera de los experimentos conocidos.
Examinando la tercera ecuación, se observa un término que describe la generación de un campo eléctrico por un campo magnético variable. ¿Por qué no debería tener la cuarta ecuación un término análogo que describiese la generación de un campo magnético por un campo eléctrico variable?
La hipótesis de Maxwell fue que al segundo miembro de la ley de Ampère había que agregarle un término con dimensiones de densidad de corriente y tal que cumpliera que la divergencia de la densidad de corriente total fuera nula. Por tanto, la divergencia del nuevo miembro debía ser igual a la variación temporal de la densidad de carga eléctrica.
En efecto, con la constante apropiada, el nuevo término añadido a la cuarta ecuación era consistente con el principio de conservación de la carga eléctrica. Es más, esta constante era lo suficientemente pequeña como para que Maxwell pudiese insertar el nuevo término sin introducir resultados que fueran contradictorios con cualquiera de los experimentos conocidos.
Con el nuevo término llamado corriente de desplazamiento las ecuaciones de Maxwell quedaron completas. Las disciplinas de la electricidad y el magnetismo quedaron unificadas por medio de una descripción elegante y consistente de los fenómenos electromagnéticos.
Ondas Electromagnéticas
Pronto se descubrió que las ecuaciones de Maxwell, con el nuevo formalismo, predecían las ondas electromagnéticas de todas las frecuencias, generadas de forma predecible por cargas eléctricas aceleradas. Además, la velocidad de propagación para todas esas ondas era la de la luz independientemente de la frecuencia.

Ecuación de Onda Electromagnética para los campos eléctrico y magnético

Ecuación de Onda Electromagnética para los campos eléctrico y magnético
Las leyes de Maxwell confirmaron que la luz visible era una onda electromagnética dentro de una banda de frecuencia determinada. Además, estas ecuaciones requerían ondas de frecuencia mayor (ultravioleta, rayos X y rayos gamma) y menor (infrarrojo, microondas, ondas de radio). Estas formas de radiación electromagnética fueron progresivamente descubiertas experimentalmente.
Energía de una Onda Electromagnética
El flujo de potencia de una onda electromagnética por unidad de área a través de una superficie viene dada por el vector de Poynting:
P = E x H
Como los campos eléctrico y magnético son perpendiculares entre sí y perpendiculares a la dirección de propagación, el flujo de energía tiene la dirección de propagación de la onda.
Las cargas en movimiento uniforme o en reposo no radian. Para que se produzcan ondas electromagnéticas y, por tanto, radiación de energía, las cargas tienen que tener un movimiento acelerado (movimiento circular uniforme, movimiento oscilatorio, etc) porque sino el vector de Poynting no es perpendicular a la superficie que envuelve la fuente.
Potencial escalar y Potencial Vector
En el caso del campo gravitatorio el potencial es una función escalar de la que se deriva el campo mediante el gradiente. En el caso del electromagnetismo es más complicado porque puede existir un potencial escalar y un potencial vectorial.
En todos los problemas electromagnéticos, dadas unas fuentes y una región del espacio con condiciones de contorno adecuadas, se ha de buscar una solución de las ecuaciones de Maxwell.
En ciertos casos, como las ecuaciones de onda homogéneas, es posible encontrar directamente la solución de las ecuaciones. En general, no obstante, es más conveniente utilizar los potenciales como funciones auxiliares que simplifican la resolución de las ecuaciones, y a partir de ellas obtener los campos.
En ciertos casos, como las ecuaciones de onda homogéneas, es posible encontrar directamente la solución de las ecuaciones. En general, no obstante, es más conveniente utilizar los potenciales como funciones auxiliares que simplifican la resolución de las ecuaciones, y a partir de ellas obtener los campos.
El hecho de que el campo magnético tenga divergencia nula permite escribirlo como el rotacional del potencial vectorial:
Definiciones de los campos eléctrico y magnético en función del potencial vectorial A y del potencial escalar Φ
La expresión del campo eléctrico de la imagen anterior se ha obtenido sustituyendo la ecuación anterior en la ley de Faraday.
El campo eléctrico puede ser radial por derivar de un gradiente, en cuyo caso es conservativo. También puede ser solenoidal (líneas de campo curvas) al poder derivar de un potencial vectorial cuya divergencia sea nula.
En el caso de que el potencial vectorial sea nulo, estamos en electrostática, donde el campo eléctrico siempre es conservativo.
El campo magnético no depende del potencial escalar Φ. Es decir, en electrostática no hay campos magnéticos. Solo aparecen si hay movimiento.
Esto nos lleva a las siguientes conclusiones:
- El campo magnético es un campo residual generado por el potencial vectorial y que puede desaparecer aunque exista un campo eléctrico.
- El campo eléctrico es el campo predilecto del electromagnetismo. Puede existir en ausencia de un campo magnético, aunque en tal caso no debe variar con el tiempo.
- Las unidades del campo eléctrico (V/m) estan relacionadas con las del campo magnético (Teslas) dividiendo por la velocidad de la luz. Esto nos da indicios de que la teoría de la relatividad puede establecer una nueva relación o conexión entre ambos campos.
Leyes de Maxwell y Relatividad
La teoría del electromagnetismo dio pistas a Einstein para formular su teoría de la Relatividad Especial, porque considerando las leyes de Maxwell:
- La velocidad de la luz es constante e independiente del movimiento de la fuente o del observador. Es decir, no existe el tiempo absoluto.
- Si la masa del fotón es nula y su velocidad es la de la luz, entonces esta velocidad es un límite cósmico que no puede sobrepasarse.
- En las ecuaciones de Maxwell solo tiene importancia el movimiento relativo (es equivalente mover un imán en el interior de una bobina a dejar el imán quieto y mover la bobina).
- Son invariantes bajo transformaciones de Lorentz. Son relativisticamente invariantes porque estan expresadas en el lenguaje de los campos y la energía en lugar de las fuerzas.
- Muestran que los campos y los potenciales se propagan con una velocidad finita, evitando la acción a distancia de la mecánica newtoniana.
Por eso fueron de gran inspiracion para Albert Einstein de cara a resolver las inconsistencias de la mecánica clásica con el electromagnetismo mediante la Teoría de la Relatividad Especial (las ecuaciones de Maxwell no son invariantes bajo las transformaciones de Galileo y de ahí la propuesta de la existencia del éter luminífero que complicaba mucho la teoría).
Desde el punto de vista de la Relatividad, lo que es campo eléctrico y campo magnético depende del movimiento relativo entre el observador y el campo. Se puede encontrar una transformación de Lorentz (un observador con un movimiento relativo determinado) que intercambie el campo eléctrico por el campo magnético.
El campo magnético que ve un observador es un efecto relativista del campo eléctrico sobre otro observador en movimiento relativo. Ambos campos son dos caras del mismo ente, el campo electromagnético, que cuando no se propaga (velocidad nula entre observador y campo) muestra solo su versión electrostática.
En electromagnetismo todo son distintas percepciones de campos eléctricos fundamentales. No obstante, si los monopolos magnéticos existieran, el campo eléctrico y magnético estarían en pie de igualdad y el campo magnético no sería simplemente un efecto colateral del campo eléctrico.
El campo magnético y la fuerza de Lorentz son un apaño necesario para el observador para poder reconstruir toda la fuerza pese a que el campo eléctrico se haya modificado al variar el estado de movimiento de este. El campo magnético compensa ciertas variaciones del campo eléctrico que no se deberían producir. En general percibimos efectos magnéticos porque no siempre es posible encontrar un sistema de referencia en que todas las cargas del sistema estén en reposo.
Finalmente, desde la perspectiva de la Relatividad Especial, se pueden expresar las ecuaciones de Maxwell en notación tensorial, a partir el tensor de Faraday Fμν, requiriendo solo dos ecuaciones.
El tensor de Faraday Fμν eq se define a partir del potencial vectorial (cuadripotencial) como:
Fμν = gμβ Fβν = gμα gνβFαβ = ∂μAν - ∂νAμ
Finalmente, desde la perspectiva de la Relatividad Especial, se pueden expresar las ecuaciones de Maxwell en notación tensorial, a partir el tensor de Faraday Fμν, requiriendo solo dos ecuaciones.
Ecuaciones de Maxwell en forma tensorial. La primera ecuación agrupa la ley de Gauss y la de Ampère. La segunda ecuación agrupa la ley de Gauss para el magnetismo y la ley de Faraday
El tensor de Faraday Fμν eq se define a partir del potencial vectorial (cuadripotencial) como:
Fμν = gμβ Fβν = gμα gνβFαβ = ∂μAν - ∂νAμ
siendo gμν el tensor métrico de la Relatividad Especial.
Invariancia o simetría gauge del Electromagnetismo
Se puede comprobar por sustitución en las definiciones de los campos a partir de los potenciales que los campos eléctrico y magnético (y por lo tanto las ecuaciones de Maxwell) son invariantes bajo la transformación gauge:
Transformación gauge de los potenciales vectorial y escalar del electromagnetismo
donde Χ(r,t) es una función escalar arbitraria. En la notación tensorial de la teoría de la Relatividad y usando los conceptos de cuadripotencial, cuadriposición y espacio-tiempo de Minkowski, las dos expresiones anteriores pueden unirse en la siguiente:
Aμ = (At, Ax, Ay, Az) = (ϕ/c, Ax, Ay, Az)
Aμ = (At, Ax, Ay, Az) = (ϕ/c, Ax, Ay, Az)
A'μ = Aμ + ∂Χ/∂xμ
donde xμ = (ct, x, y z) es la cuadriposición.
Esta es una simetría fundamental del electromagnetismo que hace que, dados unos campos eléctrico y magnético, los potenciales que los describen no sean únicos. Esto sucede porque los campos electromagnéticos E y B (o D y H) se definen únicamente a partir de las derivadas de los potenciales.
Para simplificar las ecuaciones diferenciales de los potenciales que surgen de las ecuaciones de Maxwell podemos usar la invariancia gauge, llevando a cabo una fijación de gauge: dados unos potenciales ϕ, A, buscamos una función X que elimine términos. Normalmente, esto se lleva a cabo imponiendo primero una ligadura conveniente sobre los potenciales, y luego demostrando que esta siempre es posible para alguna X.
Gauge de Lorentz o condición de Lorentz
En todos los problemas electromagnéticos, dadas unas fuentes y una región del espacio con condiciones de contorno adecuadas, se ha de buscar una solución de las ecuaciones de Maxwell.
En ciertos casos, como las ecuaciones de onda homogéneas, es posible encontrar directamente la solución de las ecuaciones. En general, no obstante, es más conveniente utilizar los potenciales A y ϕ como funciones auxiliares que simplifican la resolución de las ecuaciones, y a partir de ellas obtener los campos E y B.
En ciertos casos, como las ecuaciones de onda homogéneas, es posible encontrar directamente la solución de las ecuaciones. En general, no obstante, es más conveniente utilizar los potenciales A y ϕ como funciones auxiliares que simplifican la resolución de las ecuaciones, y a partir de ellas obtener los campos E y B.
Como he comentado anteriormente, el hecho de que el campo magnético tenga divergencia nula permite escribirlo como el rotacional del potencial vectorial:
Definiciones de los campos eléctrico y magnético en función del potencial vectorial A y del potencial escalar Φ
La expresión del campo eléctrico en la imagen anterior se ha obtenido sustituyendo la ecuación del campo magnético B = ∇ x A en la ley de Faraday.
Una de las fijaciones gauge más utilizadas en electromagnetismo es el llamado gauge de Lorentz o condición de Lorentz, en el que se satisface:
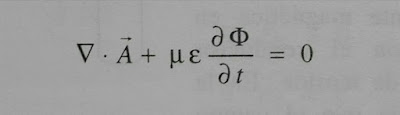
Condición de Lorentz que asigna un valor a la divergencia del potencial vectorial
Dados unos potenciales cualesquiera ϕ, A, es siempre posible encontrar una transformación gauge (una función X) tal que los potenciales transformados satisfagan la condición de gauge de Lorentz.
Sustituyendo las expresiones de los potenciales transformados según X en la ligadura de la condición de Lorentz obtenemos esta expresión que se debe cumplir para algún X. En este caso vemos que sí porque está condición se reduce a la ecuación de onda para X (con infinitas soluciones) en el caso del gauge de Lorentz
La condición de Lorentz no fija completamente el gauge, en el sentido de que hay infinitas funciones X que permiten la condición de Lorentz.
Si sustituimos las definiciones anteriores de los campos en función de los potenciales en la ley de Ampère y en la ley de Gauss tenemos:
Ecuación diferencial del potencial vectorial obtenida de las ecuaciones de Maxwell
Ecuación diferencial del potencial escalar obtenida de las ecuaciones de Maxwell
y aplicamos la condición de Lorentz mostrada anteriormente obtenemos las ecuaciones de onda para los potenciales:
Ecuaciones de onda para los potenciales vectorial y escalar
La condición de Lorentz simplifica mucho las ecuaciones diferenciales de los potenciales y es aplicable porque se ha definido el potencial vectorial únicamente mediante su rotacional, lo que permite imponerle condiciones adicionales, y en particular, fijar arbitrariamente su divergencia. De hecho la expresión del potencial vectorial puede ser cualquiera siempre que proporcione el mismo rotacional.
La expresión exacta de los potenciales no es necesario conocerla siempre porque lo que realmente describe los fenómenos electromagnéticos son los campos eléctrico y magnético. Aunque disponer de ellos puede simplificar el cálculo de los campos.
Además su expresión concreta tampoco es crucial porque, debido a la simetría gauge, hay muchos potenciales diferentes que pueden dar lugar a los mismos campos eléctrico y magnético y, por tanto, originar los mismos fenómenos electromagnéticos.
Gauge de Coulomb
En ausencia de cargas, siempre es posible imponer la condición de gauge de Coulomb:
ρ = 0 , j = 0 → ϕ = 0 , ∇·A = 0
Este es un caso particular del gauge de Lorentz pues se cumple idénticamente para ϕ = 0 y ∇·A = 0.
El gauge de Coulomb puede aplicarse en el análisis de la propagación de los campos eléctrico y magnético en el vacío (ausencia de fuentes). En este caso la ecuación diferencial del potencial vector (el potencial escalar ya sabemos que es nulo) es la ecuación de onda cuya solución es una onda senoidal.
Al obtener los campos eléctrico y magnético definidos a partir de los potenciales encontramos que estos se propagan como una onda plana.
Ecuación de Onda del potencial vectorial
Solución ondulatoria para el potencial vectorial de la ecuación de onda
Al obtener los campos eléctrico y magnético definidos a partir de los potenciales encontramos que estos se propagan como una onda plana.
Onda electromagnética plana resultado de aplicar el gauge de Coulomb
Potenciales retardados
La solución de las ecuaciones de onda para los potenciales del apartado anterior referida al sistema de coordenadas de la siguiente figura:
Sistema de coordenadas r' para las fuentes y r para los campos
toma la forma general:
Expresiones generales para los potenciales vectorial y escalar en función de las fuentes (cargas y corrientes)
En la expresión de la solución de los potenciales puede observarse un término de retardo en la variable temporal dependiente de la velocidad de propagación, que sabemos que es la de la luz. Se muestra, por tanto, como los potenciales se propagan a una velocidad finita (acorde a la Teoría de la Relatividad) y se elimina la acción a distancia de la mecánica newtoniana.








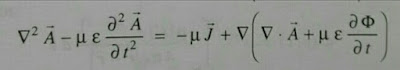


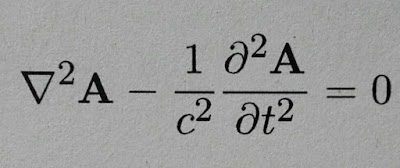




1 comentario:
Que buena síntesis, aprecio tu trabajo, gracias!.
Publicar un comentario