A continuación quería mostrar 20 ecuaciones de la física, las matemáticas y la ingeniería que considero fundamentales para el progreso de nuestro conocimiento del funcionamiento del Universo y para el desarrollo de la tecnología hasta su estado actual. Las he ordenado cronológicamente y entre ellas hay fórmulas de:
Las 20 ecuaciones son:
- Mecánica Newtoniana/clásica
- Matemáticas
- Termodinámica y Mecánica Estadística
- Electromagnetismo
- Mecánica Cuántica
- Relatividad Especial y General
- Cosmología
- Electrodinámica Cuántica
- Teoría de la Información
- Gravedad Cuántica
Las 20 ecuaciones son:
1) La Segunda Ley de Newton
2) La Ley de Gravitación Universal
3) La Fórmula de Euler
4) La Ecuación de Onda
5) La Primera Ley de la Termodinámica
6) La Segunda Ley de la Termodinámica
7) Las Ecuaciones de Maxwell
6) La Segunda Ley de la Termodinámica
7) Las Ecuaciones de Maxwell
8) La Ecuación de la Energía de Gibbs
9) La ley de Stefan-Boltzmann
10) La Entropía de Boltzmann
9) La ley de Stefan-Boltzmann
10) La Entropía de Boltzmann
11) La Energía de un Cuanto de Planck
12) Ecuaciones de la Teoría de la Relatividad
13) El Principio de mínima acción
14) La Dualidad Onda-Corpúsculo
15) El Principio de Incertidumbre
16) La Ecuación de Schrödinger
17) La Ley de Hubble
18) La Ecuación de Dirac
19) La Entropía de una Fuente
20) La Entropía de un Agujero Negro
A estas veinte ecuaciones me gustaría añadir una más muy importante aunque bastante compleja: la del Modelo Estándar de Partículas.
1) La Segunda Ley de Newton

La aplicación de una fuerza sobre un cuerpo de masa m le imprime una aceleración a
La Segunda Ley de Newton describe el movimiento de todo cuerpo no cuántico ni relativista, es decir, no microscópico y con velocidad muy inferior a la de la luz.
Esta sencilla ecuación permite plantear una ecuación diferencial para obtener la trayectoria en función del tiempo considerando que la aceleración es la derivada segunda de la posición:
En el caso de un muelle, sabemos por la Ley de Hooke que:
donde el signo menos indica que la fuerza es opuesta al desplazamiento. Así para este muelle obtenemos la ecuación diferencial:
que es la ecuación que define el movimiento armónico simple. La solución es:
Esta sencilla ecuación permite plantear una ecuación diferencial para obtener la trayectoria en función del tiempo considerando que la aceleración es la derivada segunda de la posición:
F = md²x(t)/dt²
En el caso de un muelle, sabemos por la Ley de Hooke que:
F = -Kx
donde el signo menos indica que la fuerza es opuesta al desplazamiento. Así para este muelle obtenemos la ecuación diferencial:
md²x(t)/dt² + kx = 0
que es la ecuación que define el movimiento armónico simple. La solución es:
x(t) = cos (ωt) siendo ω² = k/m
El movimiento armónico simple es muy importante porque cualquier movimiento puede descomponerse en una suma de movimientos armónicos simple gracias a la descomposición en series de Fourier.
Realmente la ecuación que propuso Newton era que la fuerza es igual a la variación del momento lineal o cantidad de movimiento (p=mv) respecto del tiempo:
Cuando la masa es constante, esta ecuación se reduce a la de la imagen anterior. Si la masa variara, como por ejemplo en un cohete, tendríamos que:
F = d(mv)/dt = vdm/dt + mdv/dt = vdm/dt + ma
A partir del concepto de fuerza se definió el de energía como el trabajo dW (elemento infinitesimal de trabajo) realizado por una fuerza aplicada sobre un objeto durante una distancia dr (el punto indica producto escalar):
Considerando la definición de fuerza anterior, tendríamos que la energía (en este caso cinética) sería:
O la energía necesaria para variar la velocidad de un cuerpo con momento lineal P.
En el caso de campos conservativos (no hay pérdidas de energía, por ejemplo, por disipación de calor) como el gravitatorio, este trabajo puede convertirse, además de en energía cinética, en energía potencial (gravitatoria).
En el caso de una fuerza constante y un desplazamiento igual a una altura h paralelo a la dirección de la fuerza, tenemos que en la superficie terrestre:
Uno de los teoremas más importantes es el de las Fuerzas Vivas (para un sistema aislado):
Realmente la ecuación que propuso Newton era que la fuerza es igual a la variación del momento lineal o cantidad de movimiento (p=mv) respecto del tiempo:
F = dP/dt
Cuando la masa es constante, esta ecuación se reduce a la de la imagen anterior. Si la masa variara, como por ejemplo en un cohete, tendríamos que:
A partir del concepto de fuerza se definió el de energía como el trabajo dW (elemento infinitesimal de trabajo) realizado por una fuerza aplicada sobre un objeto durante una distancia dr (el punto indica producto escalar):
dW = F·dr
Considerando la definición de fuerza anterior, tendríamos que la energía (en este caso cinética) sería:
dEcin = P·dv
O la energía necesaria para variar la velocidad de un cuerpo con momento lineal P.
En el caso de campos conservativos (no hay pérdidas de energía, por ejemplo, por disipación de calor) como el gravitatorio, este trabajo puede convertirse, además de en energía cinética, en energía potencial (gravitatoria).
dU = dEpot = Fgrav·dr
En el caso de una fuerza constante y un desplazamiento igual a una altura h paralelo a la dirección de la fuerza, tenemos que en la superficie terrestre:
Epot = Fgrav·dr = mgh
Uno de los teoremas más importantes es el de las Fuerzas Vivas (para un sistema aislado):
ΔW = ΔEcin + ΔEpot
A partir del concepto de energía Lagrange construyó la mecánica lagrangiana mediante las ecuaciones de Euler-Lagrange. El formalismo de Lagrange permite evitar el trabajar con vectores para solucionar determinados problemas.
2) La Ley de Gravitación Universal

Según la Ley de Gravitación Universal, la fuerza de atracción gravitatoria es proporcional al producto de las masas de ambos cuerpos e inversamente proporcional al cuadrado de la distancia que los separa
Newton formuló su famosa Ley de Gravitación basándose en las tres leyes de Kepler, que a su vez se había apoyado en los minuciosos datos recogidos por Tycho Brahe. Estas tres leyes son:
1) Las órbitas de los planetas del sistema solar tienen formas elípticas, con el Sol en uno de sus focos.
2) Al recorrer la órbita, los cuerpos barren áreas iguales en tiempos iguales.
3) El cuadrado del período de la órbita es proporcional al cubo del radio de la órbita.
Los planetas del sistema solar se mueven según la Ley de Gravitación Universal de Newton
Además de obtener una ley sencilla con un gran poder predictivo, otro de los méritos fue la unificación del movimiento de los cuerpos en la superficie de la tierra con la de los astros en el firmamento. Esta unificación resulto en un inmenso campo de aplicabilidad de esta ley.
En la superficie de la tierra, la caída de cuerpos por efecto de la gravedad es debida a su peso F=mg, donde g = 9,8 m/s² es la aceleración de la gravedad. Pero esta fórmula es una simplificación de la Ley de Gravitación Universal cuando una de las masas es la de la tierra MT, ya que:
g=GMTRT-1
La Ley de Gravitación Universal es el prototipo de ley científica: es sencilla, tiene un gran poder predictivo y un amplio campo de aplicación.
Sin embargo tiene un gran problema del que hasta Newton era consciente pero que no supo resolver: el de la acción a distancia. Esta ley no define el mecanismo físico mediante el cual dos cuerpos ejercen o sienten la atracción gravitatoria además de permitir que esta se produzca de manera instantánea.
3) La Fórmula de Euler
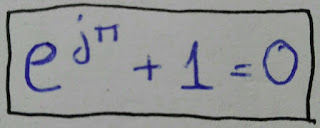
La Fórmula de Euler
Es una curiosa expresión matemática en que intervienen 5 de los números más importantes de las matemáticas, cada uno miembro de diferentes familias:
- e: número real transcendente, base de los logaritmos neperianos.
- j (o i): unidad imaginaria perteneciente a los números complejos.
- π: número real transcendente, razón entre el perímetro y el diámetro de una circunferencia.
- 1: unidad natural.
- 0: el concepto de la nada.
Realmente es un caso particular para θ=π de la fórmula:
eiθ = cos(θ) + isen(θ)
de un amplio uso en ingeniería, sobretodo en el análisis de fenómenos ondulatorios mediante el análisis y la transformada de Fourier.
4) La Ecuación de Onda
Ecuación de Onda particularizada para una velocidad de propagación de la onda igual a la de la luz (vp = c)
Puede comprobarse que todo movimiento periodico satisface esta ecuación:
u(x,t) = u(x-vpt,t)
Como por ejemplo el caso particular de ondas senoidales. Usando la fórmula de Euler anterior, el caso particular de una onda senoidal podemos expresarla como:
ψ(x,t)= u(x,t)=Aei(kx-ωt)
5) La Primera Ley de la Termodinámica
5) La Primera Ley de la Termodinámica
El incremento de energía interna o entalpía del sistema es igual al calor menos el trabajo extraído del sistema
También conocida como principio de conservación de la energía para la termodinámica, la formuló Carnot en 1824 y establece que si se realiza trabajo sobre un sistema o bien este intercambia calor con otro, la energía interna del sistema cambiará.
Visto de otra forma, esta ley permite definir el calor como la energía necesaria que debe intercambiar el sistema para compensar las diferencias entre trabajo y energía interna.
ΔEInterna = EEntra - ESale
6) La Segunda Ley de la Termodinámica
La cantidad de entropía en el Universo tiende a aumentar con el tiempo
siendo un elemento infinitesimal de entropía para procesos reversibles:
dS = dQ/T
Si además el proceso es isotermico, entonces:
También establece, en algunos casos, la imposibilidad de convertir completamente toda la energía de un tipo a otro sin pérdidas. De esta forma, el segundo principio impone restricciones para las transferencias de energía que hipotéticamente pudieran llevarse a cabo teniendo en cuenta solo el primer principio.
Gas ideal
Un gas ideal es aquel en que las moléculas no interaccionan entre sí y cuyos choques son totalmente elásticos, es decir, el incremento de temperatura es únicamente debido al aumento de la energía cinética de las moléculas y no por disipación de calor. En este caso no hay variación interna de la energía del sistema, con lo que aplicando la primera ley de la termodinámica:
Para los gases ideales existe una ecuación que relaciona algunas variables de estado que lo describen (aquellas que solo dependen de los estados inicial y final):
siendo kB =nR la constante de Boltzmann y N el número de Avogadro.
En un gas ideal no hay disipación de calor, con lo que el proceso es reversible y la entropía no varía manteniéndose constante:
En el caso de un gas ideal:
ΔS = Q/T
Gas ideal
Un gas ideal es aquel en que las moléculas no interaccionan entre sí y cuyos choques son totalmente elásticos, es decir, el incremento de temperatura es únicamente debido al aumento de la energía cinética de las moléculas y no por disipación de calor. En este caso no hay variación interna de la energía del sistema, con lo que aplicando la primera ley de la termodinámica:
AU = 0 = Q -W
Q = W = PV
Q = W = PV
Para los gases ideales existe una ecuación que relaciona algunas variables de estado que lo describen (aquellas que solo dependen de los estados inicial y final):
PV = nRT
O bien
PV = NkBT
siendo kB =nR la constante de Boltzmann y N el número de Avogadro.
En un gas ideal no hay disipación de calor, con lo que el proceso es reversible y la entropía no varía manteniéndose constante:
Si dQ = 0, entonces dS = 0 y S = constante
En el caso de un gas ideal:
S ~ PV/T = NkB = constante
En principio las leyes de la naturaleza son reversibles en el tiempo. Es decir, un determinado suceso permitido por una ley física puede ocurrir tanto hacia adelante en el tiempo como hacia atrás.
Sin embargo, siempre observamos que ocurren en la misma dirección que identificamos con el futuro. Esta dirección es la misma en la que se produce el flujo de calor. Además, en estos casos los procesos no son reversibles, como aquellos donde hay fricción. Esto es debido a la casi unidireccionalidad que establece el hecho de que la entropía media del Universo siempre aumenta. Esta ley es la que orienta la Flecha del tiempo hacia el futuro.
Sin embargo, siempre observamos que ocurren en la misma dirección que identificamos con el futuro. Esta dirección es la misma en la que se produce el flujo de calor. Además, en estos casos los procesos no son reversibles, como aquellos donde hay fricción. Esto es debido a la casi unidireccionalidad que establece el hecho de que la entropía media del Universo siempre aumenta. Esta ley es la que orienta la Flecha del tiempo hacia el futuro.
7) Las Ecuaciones de Maxwell
7) Las Ecuaciones de Maxwell
Ecuaciones de Maxwell
Ecuaciones de Maxwell en notación tensorial donde Fμν es el tensor electromagnético y jν la cuadricorriente
Las Leyes de Maxwell constituyen la primera gran unificación de las fuerzas físicas, mostrando que la electricidad y el magnetismo están íntimamente relacionados.
De ellas se obtuvo la predicción de la existencia de las ondas electromagnéticas desplazándose a la velocidad de la luz, siendo la luz una de dichas ondas.
Esto motivó la invención de la radio, del radar, de la televisión, de las conexiones inalámbricas para los ordenadores y el desarrollo de las comunicaciones modernas.
Además fueron de gran inspiracion para Albert Einstein de cara a resolver las inconsistencias de la mecánica clásica con el electromagnetismo mediante la Teoría de la Relatividad Especial.
En las Ecuaciones de Maxwell solo tiene importancia el movimiento relativo (es equivalente mover un imán en el interior de una bobina a dejar el imán quieto y mover la bobina) y las ondas se propagan a una velocidad constante independientemente de la velocidad de la fuente o del observador.
8) La Ecuación de la Energía de Gibbs
8) La Ecuación de la Energía de Gibbs
Es la variación de energía libre de Gibbs para un proceso a temperatura y presión constantes
En termodinámica, la energía libre de Gibbs (energía libre o entalpía libre) da la condición de equilibrio y de espontaneidad para una reacción química (a presión y temperatura constantes).
La energía libre es:
G = H -TS
donde H es la entalpía, T es la temperatura y S es la entropía del sistema. Fue desarrollada en los años 1870 por el físico-matemático estadounidense Williard Gibbs.
- La condición de equilibrio es ΔG es igual a 0.
- La condición de espontaneidad es ΔG mayor que cero.
- El proceso no es espontáneo cuando ΔG es menor que cero.
Esta última condición nos dice que la reacción no se producirá si no se proporciona un aporte de energía mínimo.
9) La Ley de Stefan-Boltzmann
La ley de Stefan-Boltzmann dice que la energía emitida por un cuerpo negro por unidad de área y por unidad de tiempo es proporcional a la cuarta potencia de la temperatura absoluta de su superficie
Esta ley se basa en:
- La entropía es la medida del número de microestados posibles de un sistema.
- El equilibrio térmico es un estado de máxima entropía.
- La cuantización de la energía de Planck.
- La teoría electromagnética de Maxwell.
- La distribución de Planck de la energía radiada por un cuerpo negro en función de su frecuencia y temperatura. La fórmula de Stefan-Boltzmann es la suma (o integral) de esta distribución para todas las frecuencias.
Sigma σ es la constante de Stefan-Boltzmann y es igual a:
σ=2π5k4/15c²h³
Mediante esta ley se determinó por primera vez la temperatura de la superficie del Sol y es utilizada para calcular la temperatura y el radio de las estrellas asumiendo que emiten radiación como un cuerpo negro. Para ello miden su luminosidad y despejan el radio y/o la temperatura de la fórmula siguiente:
Por tanto, con la ley de Boltzmann, los astrónomos pueden inferir los radios de las estrellas fácilmente. La ley también se usa en la termodinámica de un agujero negro en la llamada radiación de Hawking.
10) La Entropía de Boltzmann
Es una ley fundamental de la mecánica estadística que nos dice que la cantidad de entropía de un sistema es proporcional al logaritmo natural del número de microestados posibles, siendo la constante de Boltzmann k la constante de proporcionalidad. La ecuación asume que todos los microestados tienen la misma probabilidad de aparecer.
Coloquialmente, suele considerarse que la entropía es el desorden de un sistema, es decir, su grado de homogeneidad.
La entropía también puede entenderse como el número de estados microscópicos diferentes que dejan inalterado el estado macroscópico. Si este número de estados es elevado, la entropía es alta. Por ejemplo el hielo tiene menos entropía que el agua porque a nivel microscópico está formado por cristales ordenados. No es tan homogéneo a nivel microscópico como el vapor de agua.
Si enfriamos agua reducimos su entropía a nivel local pero el trabajo necesario para enfriarla genera calor que hace que la entropía media en el universo aumente, aunque localmente disminuya.
Un ejemplo doméstico sería el de lanzar un vaso de cristal al suelo: tenderá a romperse y a esparcirse, mientras que parece imposible que, lanzando trozos de cristal, se reconstruya un vaso por sí solo. No es irreversible a nivel microscópico, sino tan altamente improbable que no sucede porque hay muchos estados para el vaso roto pero muy pocos para el vaso entero.
11) La Energía de un Cuanto de Planck
Para una frecuencia dada, la energía en la naturaleza esta cuantificada en paquetes, de forma que la energía se radia y absorbe de forma discontinua
Planck introdujo esta hipótesis de la cuantización de la energía para obtener la ley de distribución frecuencial de la energía radiada y así solucionar el problema de la radiación del cuerpo negro que decía que la energía radiada debía ser infinita. Para encontrar esta distribución Planck maximiza la entropía (usando la fórmula anterior de Boltzmann) pues ello sucede en el estado de equilibrio. Además supone que:
- La emisión de energía del cuerpo negro es efectuada por osciladores armónicos simples contenidos en él (que modelan los átomos) y que pueden vibrar en todas las frecuencias.
- La frecuencia de emisión de cada oscilador es igual a su frecuencia de vibración.
- Los osciladores son indistinguibles entre sí.
- Todos los estados de energía de todos los osciladores son equiprobables.
Como la energía de cada cuanto es proporcional a la frecuencia, si esta es elevada, la energía a esa frecuencia sería mayor que la que existe en el cuerpo que la debe radiar. Por tanto ese paquete de energía no se emite, con lo que no existe energía radiada a esa frecuencia. De esta manera, aunque el espectro de radiación sea infinito, no lo es la energía emitida.
El valor de la constante de Planck h es muy pequeño y por eso a escalas de la vida cotidiana los efectos cuánticos son imperceptibles. Si supusieramos dos valores extremos para h como 0 o infinito tendríamos:
- h=0: Caso clásico en que la energía no esta cuantizada, con lo que la energía puede radiarse de manera contínua. Es como si pudieran existir fotones con energía arbitrariamente pequeña.
- h tendiendo a infinito: En este caso para generarse un fotón por ejemplo se necesitaría una energía arbitrariamente grande, con lo que no se generarían y por tanto no se radiaría energía.
Con la cuantización de la energía se inició la Mecánica Cuántica. Primero fue el Modelo de Bohr que cuantizaba las órbitas de los electrones, luego la dualidad onda-partícula y posteriormente el Principio de Incertidumbre.
En sistemas ligados como los átomos (existe una energía potencial), la cuantización de la energía descubierta por Planck lleva a una modelización mediante matemáticas discretas. Concretamente se utilizaron en un principio matrices en cuyas posiciones se almacenaban las energías de transición entre estados. Estas energías eran lo único que se podía conocer. Al usar matrices, cuyo producto no es conmutativo, el álgebra utilizada implícitamente era no conmutativa, lo que lleva finalmente al Principio de Incertidumbre.
Posteriormente, basándose en el análisis de Fourier y en la diagonalización de matrices mediante autovalores y autovectores se demostró la equivalencia entre la mecánica matricial y la mecánica ondulatoria.
En esta última las matrices se convierten en operadores cuyas funciones propias son las funciones de onda y los autovalores el valor medio del observable asociado al operador.
En principio la Ecuación de Schrödinger proporciona funciones de onda continuas con lo que parecería que la Mecánica Ondulatoria es continua. Sin embargo, en sistemas ligados existen condiciones de contorno que la solución de la ecuación de Schrödinger debe cumplir. Y son estas condiciones las que acaban cuantizando los valores posibles de la energía como en el caso del Oscilador Armónico Cuántico o del pozo cuadrado de energía.
12) Ecuaciones de la Teoría de la Relatividad
La Equivalencia entre Masa y Energía
Equivalencia entre masa y energía proporcionada por la Teoría de la Relatividad Especial
Esta ecuación unifica los principios de conservación de la masa y la energía en uno solo: el de masa-energía. Esto permite que el número de partículas varíe convirtiéndose en energía y viceversa, que de la energía pura se cree materia, es decir, partículas. Realmente hay creación de pares, absorciones, desintegraciones, aniquilaciones con lo que el número de partículas varía.
A nivel más tangible, evidenció la cantidad de energía contenida en la materia. Mediante reacciones de fisión nuclear controladas en los reactores de las centrales nucleares, se consigue obtener estas grandes cantidades de energía para crear electricidad mediante la inducción electromagnética descubierta por Faraday.
Las Ecuaciones de la Relatividad General
Las Ecuaciones de Campo de la Relatividad General proporcionan la métrica gij a partir de una distribución de masa y energía determinada por el tensor de energía-momento Tij
Son 10 ecuaciones tensoriales independientes no lineales en derivadas parciales de segundo orden donde Rij es el tensor de Ricci y R es la curvatura escalar siendo el espacio-tiempo tetradimensional modelado como un espacio curvo de Riemann.
El espacio-tiempo curvo de la Relatividad General permite una solución, aunque altamente inestable, en que dos agujeros negros se unen formando un agujero de gusano
A partir de esta métrica gij pueden calcularse las trayectorias de los cuerpos en el seno del campo gravitatorio que esta representa como las geodésicas de este espacio de Riemann. Es decir, según la Relatividad General:
Gravedad = Curvatura
La Teoría de la Relatividad General esta construida sobre el Principio de Equivalencia (además de los postulados de la Relatividad Especial). Este principio nos dice que no es distinguible a nivel local (son equivalentes) un campo gravitatorio del movimiento acelerado uniforme.
Además, este principio implica que, a nivel local, la métrica de un espacio-tiempo curvado siempre puede aproximarse como límite por la métrica plana de Minkowski de la Relatividad Especial.
A pesar de la dificultad para resolver las ecuaciones de campo de la Relatividad General, Karl Schwarzschild fue capaz de resolverlas en 1916 para una situación altamente simétrica después de que Einstein las propusiera en 1915.
Se trataba del caso del campo gravitatorio, o métrica del espacio-tiempo, generado por un cuerpo estático y estacionario de simetría esférica. La metrica que obtuvo fue:
ds² = c²(1 - rs/r)dt² - (1 - rs/r)-1dr² - r²(dθ² + sin²(θ)dφ²)
donde rs=2GM/c² es el radio de Schwarzschild y las componentes de la métrica son:
- g11 = (1 - rs/r)
- g22 = (1 - rs/r)-1
- g33 = r²
- g44 =r²sin²(θ)
Para el caso del sol, rs es igual a 3 kilómetros. Y en el caso de la tierra es de 1 milímetro. En ambos casos el volumen del Sol y de la Tierra envuelve este radio, con lo que no existe un agujero negro.
Parece que las matemáticas fallan para r=rs pero es solo una mala elección de las coordenadas. Donde sí fallan las matemáticas de la Relatividad General es para r = 0, donde existe una singularidad. Para descubrir que ocurre en el centro del agujero negro necesitamos una teoría de Gravedad Cuántica satisfactoria.
13) El principio de mínima acción
El principio de mínima acción nos dice que la trayectoria que siguen los cuerpos es aquella que hace que la acción S sea mínima.
El Principio de mínima acción nos dice que las ecuaciones de movimiento surgen de minimizar una magnitud física llamada acción
donde la acción se define como:
Definición de la magnitud física llamada acción como la integral temporal del lagrangiano
Este principio podría considerarse como una generalización del principio de Fermat, quien propuso que la luz siempre sigue la trayectoria que une dos puntos con el tiempo mínimo. Pero su origen puede estar en Maupertuis en el siglo XVIII. Euler y Leibniz desarrollaron la idea y Lagrange y Hamilton lo usaron como la base de las formulaciones lagrangiana y hamiltoniana de la mecánica clásica.
No obstante no fue hasta la formulación de la mecánica cuántica que este principio mostró todo su potencial, convirtiéndose en esencial en las Teorías Cuánticas de Campos.
Las ecuaciones de Euler-Lagrange obtenidas mediante el cálculo de variaciones son la solución que hace que L minimice la acción
La utilización de los conceptos de Lagrangiano y principio de mínima acción permite solucionar problemas de manera más sencilla con el concepto de energía (magnitud escalar) en lugar del de fuerza (magnitud vectorial).
Además, debido al teorema de Noether (a cada simetría le corresponde una magnitud conservada), es útil formular las leyes de movimiento en función del Lagrangiano porque este hace visibles las simetrías del sistema, y por tanto, las magnitudes que en este se conservan.
Por ejemplo, en el movimiento en el seno de un campo gravitatorio, el lagrangiano es:
L = ½mvy² - mgy
Aplicando las ecuaciones de Euler-Lagrange obtenemos:
-mg -d(mvy)/dt = 0
mg = dpy/dt
que es la segunda ley de Newton.
14) La Dualidad Onda-Corpúsculo
La longitud de Onda de De Broglie es igual a la constante de Planck dividida por la cantidad de movimiento de la partícula y evidencia la naturaleza ondulatoria de la materia
Toda partícula o cuerpo tiene una longitud de onda asociada igual al cociente entre la constante de Planck y su momento lineal.
Si la masa es mucho mayor que h, la longitud de onda se aproxima a cero (no existe onda asociada). Por eso los efectos extraños de la Mecánica Cuántica no se manifiestan en nuestra vida real.
Sin embargo, a nivel microscópico las partículas pueden comportarse como ondas, como se comprobó con el experimento de la doble rendija de Young en 1803. Este experimento reveló la naturaleza ondulatoria del electrón y que este está sujeto a fenómenos de interferencia.
Fenómeno de interferencia en el experimento de la doble rendija
15) El Principio de Incertidumbre
Existe un límite inferior al producto de las incertidumbres en la posición y en el momento lineal igual a la constante de Planck dividida entre 2π
El Principio de Incertidumbre marca un antes y un después en la historia de la física, provocando la rotura con la física clásica. Es lo que realmente hace diferentes a la mecánica clásica de la Mecánica Cuántica.
Además es lo que genera la incompatibilidad entre la Relatividad General y la Mecánica Cuántica imposibilitando la obtención de una Teoría de Gravedad Cuántica.
Este principio formulado por Heisenberg es la esencia de la Mecánica Cuántica y lo que origina un frenesí a nivel microscópico permitiendo la creación de pares de partículas acorde con la equivalencia de masa-energía de la Relatividad Especial. Este principio es también el responsable del efecto túnel.
La constante de Planck introducida por el físico alemán en el año 1900 es, por tanto, la medida universal de la indeterminación introducida en las leyes naturales por el dualismo onda-corpúsculo.
16) La Ecuación de Schrödinger
Ecuación de Schrödinger donde H es el operador hamiltoniano
Fue postulada como una ecuación de autovalores del operador Hamiltoniano para la función de onda, siendo el autovalor E la energía asociada a una configuración estable o permitida del sistema.
Hψ = Eψ
Para obtenerse la ecuación de Schrödinger se deben sustituir el operador H y el autovalor E por los operadores cuánticos correspondientes, siendo H:
H = p²/2m + V
El módulo al cuadrado de la función de onda proporciona la probabilidad de encontrar a la partícula en una cierta posición. Esta función de onda esta sujeta a fenómenos ondulatorios como la interferencia.
Aplicando los operadores cuánticos asociados a los observables de la posición, energía, momento lineal, energía cinética o momento angular podemos conocer los valores de estas magnitudes a partir de la función de onda.
Entre los defectos de la ecuación de Schrödinger están el no ser válida para partículas con masa nula y el no ser relativista porque:
- En ella nada impide ir más rápido que la luz.
- El tiempo y el espacio no son tratados por igual pues aparece la derivada primera respecto del tiempo pero segunda respecto al espacio.
- Aparece la definición clásica de energía cinética en lugar de la energía relativista.
Además en la ecuación de Schrödinger el número de partículas es estable. Sin embargo realmente hay creación de pares, absorciones, desintegraciones, aniquilaciones con lo que el número de partículas varía. Esto es consecuencia de la conservación/equivalencia masa-energía de la Relatividad Especial.
17) La Ley de Hubble
La Ley de Hubble nos dice que la velocidad de alejamiento de las galaxias es proporcional a la distancia que las separa, siendo la constante de Hubble H la constante de proporcionalidad
Como representación de la cosmología, la ley de Hubble sorprendió mucho cuando fue formulada por Edwin Hubble en 1929 ya que casi nadie imaginaba que el Universo realmente se estuviera expandiendo. Constituye la principal prueba del Modelo del Big Bang.
Modelo del Big Bang en el que el Universo se expande tras originarse en un punto de volumen nulo y densidad infinita
Sin embargo, como demostro Friedmann, existe una solución de las Ecuaciones de la Relatividad General de Einstein que lo permiten bajo unas hipótesis de muy fácil cumplimiento (El Principio Cosmológico).
En 1998 unos experimentos con supernovas mostraron que la expansión del Universo se está acelerando, con lo que la constante de Hubble realmente no es constante y varía con el tiempo, aunque muy lentamente.
18) La Ecuación de Dirac
La Ecuación de Dirac es la ecuación de onda relativista para el electrón y constituye la ley fundamental de la Mecánica Cuántica Relativista
A partir de la ecuación para la energía relativista:
E² = (pc)² + (mc)²
Se propuso la ecuación de Klein-Gordon aplicando los operadores cuánticos correspondientes a la cantidad de movimiento p y a la energía E.
Esta ecuación trata por igual el espacio y el tiempo y esta derivada a partir de la energía relativista. Sin embargo a pesar de ser relativista, presenta problemas como el de proporcionar probabilidades negativas, permitir partículas con energías negativas o no proporcionar el espectro del átomo de Hidrógeno.
Lápida sobre el sepulcro de Dirac con su famosa ecuación
Dirac resolvió el problema obteniendo una ecuación relativista que sería el origen de las Teorías Cuánticas de Campos como la Electrodinámica Cuántica. Predijo la existencia de la antimateria y la propiedad relativista del spin aparece en ella de manera natural.
19) La Entropía de una Fuente
Entropía de Shannon o información media de una fuente medida en bits. Se considera el logaritmo en base 2 porque se supone código binario
En el ámbito de la teoría de la información la entropía, también llamada entropía de la información y entropía de Shannon (en honor a Claude E. Shannon), mide la incertidumbre o aleatoriedad de una fuente de información.
Si consideramos un mensaje que puede ser generado con x símbolos diferentes cuya probabilidad es p(x), entonces la información máxima que una fuente puede transmitir a través de este mensaje viene dada por la fórmula de Shannon.
La entropía también se puede considerar como la cantidad de información promedio que contienen los símbolos usados. Los símbolos con menor probabilidad son los que aportan mayor información. Cuando todos los símbolos son igualmente probables, todos aportan información relevante y la entropía es máxima.
Esta información es máxima cuando todos los símbolos son equiprobables. Tiene lógica, pues cuando todos los símbolos tienen la misma probabilidad de ser enviados, el grado de incertidumbre (o de entropía) es máximo y también es, por tanto, la información obtenida al recibir el mensaje.
En el caso de un código con dos símbolos equiprobables, p(x)=1/2 para ambos y H=1 (1 bit de información) es máxima
En el caso de 3 símbolos con probabilidades ½, ¼ y ¼, tendríamos que H=1,5, lo que significa que necesitamos una media de 1,5 bits para enviar un símbolo. Esto pone un límite inferior a la compresión que podemos hacer a un mensaje generado por esta fuente.
En el caso de 4 símbolos equiprobables, tendríamos que H=2, lo que significa que la recepción de un símbolo aporta 2 bits de información y que necesitamos un mínimo de 2 bits para codificar todos los símbolos, que podrían ser:
00, 01, 10, 11
La fórmula de Shannon establece, por tanto, un límite a la compresión de la información. Una codificación menos eficiente sería:
0001, 1101, 0010, 1111
En el caso del siguiente mensaje de 16 bits codificado con 2 bits por símbolo tenemos:
11 10 00 00 00 00 00 01
S4 S3 S1 S1 S1 S1 S1 S2
La entropía en este caso es:
H = 1/8*3+1/8*3+1/8*3+5/8*(3-2.32)= 1,55
Por tanto este mensaje contiene en realidad:
1,55 bits/símbolo*8símbolos= 12,4bits
Si intentamos optimizar la codificación con símbolos de longitud variable como por ejemplo:
0,1, 10, 11, 100, 101, 110,111
Entonces el mensaje se envía en secuencias de dos símbolos. El primero nos dice cuantos bits iguales vienen detrás y el segundo si ese bit es un 0 o un 1.
El mensaje resultante es:
11 1 111 0 101 0 1 1
Hemos conseguido reducir de 16 a 13 bits utilizando una codificación más inteligente quedándonos a 0,6 bits del mínimo marcado por la fórmula de Shannon.
Un codificador óptimo es aquel que utiliza el mínimo número de bits para codificar un mensaje. Un codificador óptimo usará códigos cortos para codificar mensajes frecuentes y dejará los códigos de mayor longitud para aquellos mensajes que sean menos frecuentes. De esta forma se optimiza el número de bits para representar el mensaje.
Por ejemplo, el código Morse se aprovecha de este principio para optimizar el número de caracteres a transmitir a partir del estudio de las letras más frecuentes del alfabeto inglés.
En el caso de una fotografía, un archivo de sonido o un vídeo se dan muchas repeticiones de bits (zonas de color uniforme de una imagen, silencio en un archivo de audio) que si no se codifican eficientemente provoca que enviemos más bits de los necesarios para la correcta recepción del mensaje.
20) La Entropía de un Agujero Negro
La entropía de un agujero negro es proporcional a un cuarto del área A del horizonte de sucesos en unidades de Planck
Esta ecuación es uno de los primeros éxitos en combinar la Relatividad General con las Teorías Cuánticas de Campos basadas en la Mecánica Cuántica. Es decir, es uno de los primeros resultados de la Gravedad Cuántica.
Contra lo que se pueda pensar, un agujero negro tiene entropía, y por tanto una temperatura. Y si tiene temperatura debe radiar y evaporarse
Pero un agujero negro es una región del espacio-tiempo vacío entre el horizonte de sucesos y la singularidad porque toda la materia absorbida es triturada por los gradientes gravitatorios extremos. Entonces,¿cómo algo vacío puede tener entropía? Porque realmente si hay algo: energía. La materia despedazada es convertida en energía que queda confinada.
Si hay entropía, entonces hay desorden y por tanto energía cinética. Con energía cinética hay temperatura, y todo cuerpo con temperatura radia. Así que los agujeros negros no son tan negros. A esta radiación se la conoce como Radiación de Hawking.
La entropía también es una medida de la información contenida en un sistema físico. Si, por ejemplo, comenzáramos a amontonar grandes cantidades de información de cualquier tipo (digital en discos duros o DVDs y física en forma de mobiliario, piedras, lo que sea) llegaríamos a un punto en que ya no cabe nada más. Ese punto sería el de la formación de un agujero negro con un horizonte de sucesos igual a la superficie que limitaba nuestra región inicial de acumulación de información. Esta información sería igual a la entropía del agujero negro dada por la fórmula anterior. Si siguiéramos añadiendo información, el horizonte crecería.
Lo chocante de esta ecuación, además de revelar que en un agujero negro cabe una cantidad inimaginable de información, es que nos dice que la cantidad de información que cabe en un agujero negro no es proporcional al volumen de este, sino al área de la superficie que lo delimita. Esto esta relacionado con el Principio Holográfico, una de las mayores revoluciones de la física teórica actual.
Otra conclusión es que en Gravedad Cuántica la Teoría de la Información tiene un papel principal junto con la Relatividad General y la Mecánica Cuántica.
Si la masa M arrojada en una región es mayor que c²R/2G, entonces se crea un agujero negro. Es un límite muy elevado. Por ejemplo 5 discos duros de 1 Tb caben en una circunferencia de radio r menor que 0,5m. Pero en esa región cabrían 1070 bits, tanta como celdas de Planck caben en el horizonte de sucesos, muchos más bits que los 5·10¹² de los cinco discos duros juntos.
Ecuación del Modelo Estándar
Finalmente quería mostrar la Lagrangiana del Modelo Estándar que condensa toda la física conocida menos la relacionada con la gravedad. Incluye por ejemplo la ecuación de Dirac y las ecuaciones de Maxwell.
Lagrangiana (abreviación de densidad lagrangiana) completa del Modelo Estándar de Partículas donde h.c. quiere decir hermítico conjugado.
Aplicando el principio de mínima acción pueden obtenerse las ecuaciones del movimiento de cualquier partícula sometida a cualquier fuerza salvo la gravitatoria.



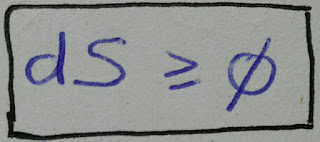











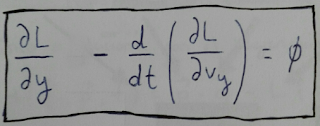








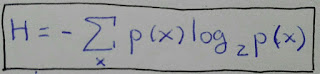




No hay comentarios:
Publicar un comentario